

Die gewöhnliche arithmetische Rechnung erfolgt gemäß der Progression von zehn mal zehn. Wir verwenden zehn Zeichen, die 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, die null, eins und die folgenden Zahlen bis einschließlich neun bedeuten.
Und dann gehen wir zur Zehn, wir fangen wieder von vorn an, und wir schreiben zehn mal zehn bis hundert (100), dann zehn mal hundert bis tausend (1000), und zehn mal tausend bis 10000 ... und so weiter.
Aber statt der Progression von zehn nach zehn verwende ich seit mehreren Jahren die einfachste Progression von allen, die von zwei nach zwei geht, da ich festgestellt habe, dass sie der Vervollkommnung der Wissenschaft der Zahlen dient.
Also verwende ich keine anderen Zeichen als 0 und 1, und dann gehe ich zu zwei [gleich 10] und fange wieder von vorne an.
Deshalb wird hier zwei als 10 geschrieben, und zweimal zwei oder vier als 100, und zwei mal vier oder acht als 1000, und zweimal acht oder sechzehn als 10000, und so weiter. Hier ist die Tabelle der Zahlen so, dass wir so lange fortfahren können, wie wir wollen.
Wir sehen hier auf einen Blick den Grund für eine berühmte Eigenschaft der verdoppelten geometrischen Progression in ganzen Zahlen, was bedeutet, dass wir, wenn wir nur eine dieser Zahlen von jedem Grad haben, alle anderen ganzen Zahlen unterhalb des doppelten höchsten Grades zusammensetzen können.
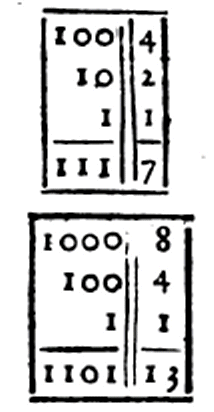
Denn hier ist es so, als würden wir zum Beispiel sagen, dass 111 oder 7 die Summe aus vier, zwei und eins ist. Und die 1101 oder 13 ist die Summe von acht, vier und eins. Diese Eigenschaft ist für [Eichungs-] Prüfer nützlich, um alle Arten von Massen mit wenigen Gewichten zu wiegen, und könnte bei Münzen verwendet werden, um mit wenigen Münzen mehrere Werte anzugeben. Die Zusammenstellung der Zahlen macht es sehr einfach, alle Arten von Operationen durchzuführen.
Und all diese Operationen sind so einfach, dass Sie nie etwas versuchen oder erraten müssen, wie Sie es bei der gewöhnlichen Division tun müssen.
Auch brauchen wir hier nichts auswendig zu lernen, wie es beim gewöhnlichen Rechnen nötig ist, wo man zum Beispiel wissen muss, dass 6 und 7 zusammen 13 ergeben; und dass 5 mit 3 multipliziert 15 ergibt.
Nach der Tabelle ist einmal eins gleich eins, was pythagoräisch genannt wird. Aber hier wird all das auf ursprüngliche Weise gefunden und bewiesen, wie man bei den obigen Beispielen bei den Zeichen ☽ [Addition] und ☉ [Multiplikation] sieht.
Ich empfehle jedoch diese [binäre] Art des Zählens nicht, [und ich empfehle auch nicht] sie statt der üblichen Praxis bis zehn einzuführen.
Denn abgesehen davon, dass wir daran gewöhnt sind, müssen wir nicht nach dem suchen, was wir schon auswendig gelernt haben: Die Zehnerübung ist verkürzter und die Zahlen sind dort kürzer. Und wenn man daran gewöhnt wäre, mit zwölf oder mit sechzehn zu rechnen, hätte man noch mehr Vorteile.
Aber das Rechnen mit zwei Werten, also mit 0 und mit 1, als Kompensation für deren [große] Länge, ist das grundlegendste für die Wissenschaft, und es gibt neue Entdeckungen, die dann nützlich sind, sogar für die Praxis der Zahlen, und vor allem für die Geometrie, deren Grund darin besteht, dass die Zahlen, wenn sie auf die einfachsten Prinzipien wie 0 und 1 reduziert werden, insgesamt eine wunderbare Ordnung darstellen.
Zum Beispiel sehen wir in der Tabelle der Zahlen in jeder Spalte Perioden, die immer wieder von vorne beginnen. In der ersten Spalte ist es 01, in der zweiten 0011, in der dritten 00001111, in der vierten 0000000011111111, und so weiter.
Wir haben kleine Nullen in die Tabelle gesetzt, um die Lücke am Anfang der Spalte zu füllen und diese Perioden besser zu kennzeichnen. In die Tabelle sind auch Linien eingezeichnet, die kennzeichnen, dass das, was diese Linien enthalten, immer darunter zurückkommt.
Auch [im Binärsystem] kommen die Potenzen drei, vier und andere Potenzen vor; auch die Dreieckszahlen, Pyramiden und andere Figurenzahlen haben ähnliche Perioden: so starke, dass man ohne zu rechnen sofort die Tabellen daraus schreiben kann.
Eine Weitläufigkeit am Anfang, die dann die Möglichkeit gibt, sich die Berechnung zu ersparen und per Regel ins Unendliche zu gehen, ist unendlich vorteilhaft.
Überraschend an dieser Berechnung ist, dass diese Arithmetik von 0 und 1 zufällig das Geheimnis der Linien eines alten Königs und Philosophen namens Fohy enthält, von dem angenommen wird, dass er vor mehr als viertausend Jahren gelebt hat und den die Chinesen als den Gründer ihres Imperiums und ihrer Wissenschaften ansehen.
Ihm werden mehrere Linienfiguren zugeschrieben. Sie kommen alle aus der [binären] Arithmetik. Es reicht aus, hier an acht Cova [katalanisch: Höhlen] wie sie genannt werden, das Grundlegende zu zeigen. Und eine Erklärung hinzuzufügen, die sie manifestiert. Vorausgesetzt, wir bemerken erstens, dass eine ganze Linie — die Eins oder 1 bedeutet, und zweitens, dass eine unterbrochene Linie – – die Null oder 0 bedeutet.
Die Chinesen wissen seit vielleicht tausend Jahren nicht mehr, was die Cova oder Linienfiguren von Fohy bedeuten. Aber sie machten Kommentare dazu, in denen sie nach einem ich weiß nicht wie weit verborgenen Sinn für diese Zeichen suchten. Nun wird ihnen die wahre Erklärung von den Europäern geliefert.
Vor kaum mehr als zwei Jahren teilte ich dem berühmten R. P. Bouvet - Jesuiten François, der in Peking lebt, meine Art, mit 0 und 1 zu zählen mit. Er erkannte sofort, daß dies der Schlüssel zu den Zahlen von Fohy ist.
So schickte er mir am 14. November 1701 in einem Schreiben die große Figur dieses königlichen Philosophen, die bis 64 [genauer von 0...63] geht und die keinen Raum mehr lässt, an der Wahrheit unserer Interpretation zu zweifeln. Man kann also sagen, dass dieser Pater das Rätsel von Fohy, mit dem, was ich ihm mitgeteilt hatte, entschlüsselt hat.
Und da diese Figuren vielleicht das älteste Denkmal der Wissenschaft der Welt sind, erscheint die Wiederherstellung ihrer Bedeutung nach so langer Zeit umso denkwürdiger.
Die Übereinstimmung der Figuren von Fohy und meiner Zahlentabelle [Table des Nombres] ist besser zu sehen, wenn man in der Tabelle die anfänglichen Nullen ergänzt, die eigentlich überflüssig erscheinen, aber dazu dienen, die Periode der Spalten besser zu markieren.
Ich habe sie deshalb [in der "Table des Numbres"] mit kleinen Kreisen ergänzt, um sie von den notwendigen Nullen zu unterscheiden. Dieser Ansatz gibt mir eine großartige Vorstellung von der Tiefe von Fohys Meditationen. Denn was uns heute leicht erscheint, war in jenen fernen Zeiten nicht so einfach.
Solange wir darüber nachdenken, ist binäre oder dyadische Arithmetik heute in der Tat sehr einfach, denn unsere Art zu zählen hilft uns sehr, nur den Übertrag zu notieren.
Die gewöhnliche Zehner-Arithmetik scheint nicht so alt zu sein. Die Griechen und Römer kannten sie [noch] nicht und wurden so um deren Vorteile gebracht. Es scheint, dass Europa deren Einführung dem Gerbert verdankt, Papst mit Namen Sylvester II, der sie von den Mauren von Spanien bekam.
Da jedoch in China immer noch angenommen wird, dass Fohy der Autor der gewöhnlichen chinesischen Schriftzeichen ist, obwohl sie sich im Laufe der Zeit stark verändert haben, lässt uns sein Essay d'Arithmetique zu dem Schluss kommen, dass darin immer noch etwas Bemerkenswertes durch die Beziehung gefunden werden könnte zu Zahlen und Ideen, um die Grundlagen der chinesischen Schrift aufzudecken. Zumal man in China glaubt, dass man Zahlen bei der Erstellung [der Schrift] berücksichtigt hat. R. P. Bouvet ist sehr geneigt, diesen Punkt voranzutreiben, und sehr fähig, dies in vielerlei Hinsicht zu erreichen.
Ich weiß jedoch nicht, ob es jemals in der chinesischen Schrift einen Vorteil gegeben hat, der dem nahe kommt, was notwendigerweise in einem von mir projizierten Merkmal enthalten sein muss:
Es ist so, dass jede Begründung, die aus Begriffen gezogen werden kann, durch Berechnung aus ihren Eigenschaften gezogen werden könnte, was eines der wichtigsten Mittel wäre, um dem menschlichen Verstand zu helfen.
l703. M
Übersetzung EXPLICATION DE L‘ARITMÈTIQUE BINAIRE. PAR M. LEIBNITZ. Abgedruckt im Band: HISTOIRE DE L‘ACADEMIE ROYALE DES SCIENCES. Année MDCCIII.
Übersetzt und ins WWW gestellt am 27. Febr. 2023 von Dr. Gerd Heinz (info@gheinz.de). Mit Erläuterungen und Kommentaren unter diesem Link http://www.gheinz.de/news/leibniz.htm.
Unterstützung gaben Rolf Tammer und Google-Translate. Herzlichen Dank für die Hilfe bei der Suche nach der Quelle an Dr. Sven Erdner von der Gottfried-Wilhelm-Leibniz-Gesellschaft (GWLB-NLB) Hannover. Nicht zuletzt großen Dank an Google http://books.google.com für den Scan des Leibnizschen Originals. Der Name "PAR M. LEIBNITZ" und das Kürzel "l703. M" geben Rätsel auf. Hat der Schriftsetzer versehentlich ein handschriftliches "W" als "M" interpretiert?
Hinweis: [Kommentare sind in eckige Klammern gesetzt]
© Copyrights: If not otherwise noted, pages are "open source". Non-commercial usage without modification is allowed with the name of the author and the URL in writing. Commercial redistribution needs the permission of author in writing. No guaranties for partial rights of third parties.
> zurück <
Gesamtzahl der Besucher auf www.gheinz.de: