
It is hard, to describe properties of wave-like movements on paper. So Andrew Packard asked in 1998 the author Gerd Heinz, if it is possible to publish his video-films with some comments on a homepage. This page is the result.
Orderly colour changes of cephalopods normally require an intact brain. When the brain has died, or the nerve supply to the skin has been removed, the colours become chaotic. Such autonomous behaviour highlights a general principle.
Andrew Packard [AP95], [AP01], [AP06], [AP11], [APgl], [GH19] has observed wave-like excitements flowing through the coloured spots (chromatophore organs) on one side of the mantle of these animals some days after cutting its nerve supply from the brain to one side of the body. These muscle-operated organs develop supersensitivity and communication between them. The different properties can be inspected directly through the animal's translucent skin.
The idea of slow flowing information in communication systems of every kind, including the nervous system, was suggested in the 1993 book by Heinz "Neuronale Interferenzen" [NI93] and has been discussed in detail in [GH94].
Andrews pictures and films show, that bio-systems are using discrete "waves", that means a wave-like distribution of pulses on nerve-wires. So his records show the basis of interference models of nerve nets.
Interesting physical "wave interference" properties, like a geometrical wave length, can be observed with our eyes, see [GH94].
After a fulfilling scientific life, Andrew Packard passed away on June 15, 2023. See also the obituary of his relatives [AP23].
Waves proceeding in a layered 'neural' wave space show relations within a single layer and between different layers. Black of different size class, and yellow chromatophores act relatively independently of each other, and with different velocities in the separate layers (see Fig.13).
Beside straight-going waves proceeding from boundaries with innervated skin, we find circular waves radiating from a centre of irritation and spiral waves rotating around a stable core.
Water temperature influences the waves. Below 6°C they are abolished. Above 10°C, frequency, velocity and numbers of waves differentially increase.
Independent moving color waves (Fig.10) show, that each color- and size class seems to have its own carrying network, although the separate innervation is little studied. It is not known by what mechanisms and through what elements the waves propagate. There is little interference between fast brown/red and yellow waves running in layers separated by only a few tens of microns and embedded in connective tissue that receives muscle fibre extensions from different layers.
The disappearance of two colliding waves in Fig.11 shows, that the conductivity mechanism acts multidirectionally. The disappearance of waves behind the locations of wave interference means that the wave space is cleaned by the refractory period of the chromatophores. The effect is known from the sciatic nerve of frogs. If two pulses are fed in from both sides, the pulse transmission stops in both directions.
Lack of any specific signalling or communication function for the various waves suggests a simple hypothesis: that the role of the conducting networks is to maintain connectivity and compliance (conformity of behaviour) amongst cells belonging to the same ontogentic class throughout the body
But however: Patterns of wave generation mostly disappear or become chaotic in the absence of external input. Left to themselves, they transmit random changes of state in one cell to cells around.

Fig.0: Centimeter scale at the squid
Fig.1: A black colour wave moves along the denervated side of a squid
Fig.2: Pressure induced waves moving from left (head) to right
Fig.3: Circular waves coming from center region
Fig.4: Straight going waves from left (head) to right
Fig.5: Circular waves coming from center region
Fig.6: Anti-clockwise turning spiral waves
Fig.7: Clockwise turning spiral waves
Fig.8: Slower wave movement induced by cold water (8°C)
Fig.9: Externally stimulated circular wave
Fig.10: Yellow and black colour waves moving independently with only weak influence on each other
Fig.11: Two waves delete by collision
Fig.12: Two waves form a new wavefront by vector addition
Fig.13: Details of Chromatophore array (screen size ~ 2x3 cm) during passage of dark and yellow waves by opening and closure of several size classes.





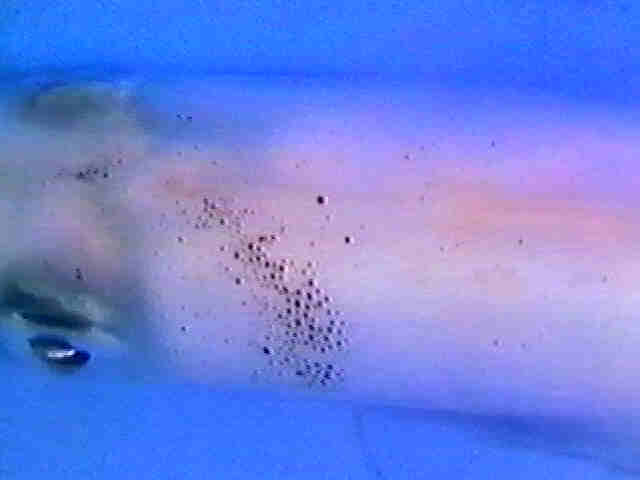












Fig.14: Picture series of the running black colour wave of Fig.1
Andrews experiments verify important parts of the theory about interference networks, published in the book "Neuronale Interferenzen" [NI93], in a simple, visible way. So these experiments are most interesting for students, who try to understand the world of information processing in biological systems.
From an anatomical view, Andrew Packard discussed the results in detail in his papers [AP95], [AP01], [AP06] and [AP11]. In short form, in physical terms the squid experiments demonstrate following effects:
Deleting waves in Fig.11 show, that we observe a kind of inhibition (signal/wave deletion) in an excitatory network. Although wave deletion appears as a kind of inhibition here, it has nothing to do with inhibiting synapses.
An one-dimensional analogy of this experiment is the effect of contra-directional stimuli in sciatic nerve of frogs. Counter waves delete themselves because periods of refractoriness (ionic depletion zones) run behind every pulse excitement and remove any counter wave.
The effect was theoretically proposed as "dynamic inhibition" in [NI93], Kap.6, S.145 and later discussed at [Bio96] or [GH04], p.5, Fig.7b.
In addition to traditional knowledge, inhibition of signals can have different other reasons:
Note, that No. 2) and 3) do not need any inhibiting substance or synapse.
Andrews Experiments offer a rule for the understanding of excitatory and inhibitory data flows. Waves from one source can only reach a destination, if they have a frequency, as the counter wave source. If the counter waves have higher frequency, no possibility exists, to propagate any wave to a destination against the counter waves.
Up to now it has been difficult to perceive the relevance of this effect for the understanding of nervous systems. If we suppose that the same effect (observed in this special system) happens between any kind of "normal" (bi-directional) nerve cells, one of many possible interpretations would be, that there can be no information flow on any pathway if it is blocked by counter waves. The waves with the higher frequency kills the counter wave, before the counter waves can propagate.
If we implement the idea formaly to nerve system, we can establish some laws:
a) A growing number of counter waves on a field reduces the communication possibilities, because most waves are destroyed by counter waves before they can reach a certain destination. The source with the highest pulse density is the winner.
b) A decreasing average pulse rate on a neural field enhances the possibility for communication between sources and destinations from different directions.
c) But: Less excitement of field neurons supposed, the probability to reach a destination encreases with the frequency of fire.
Thus, to get the best chance to bring any information (as image or sign) through a nerve system, we need the highest fire frequency (before cross-interference overflow) for a certain time. This is known as a fire-burst.
The effect can be computed in relation between geometrical impulse length, refractoriness, fire frequency and empty field size, if we compute local time functions for each cell.
For computer-simulations, wave deletion encreases the time of calculations dramatically. To calculate the effect adequate, we have to calculate each cell for each time step, overlay methods for linear superimposition does not help.
Thinking this way, nerve network theory get a different direction. Although we have an excitement-only-network (without inhibition), we only have to avoid (inhibiting) wave-blocking mechanisms to get a free runway for any (multi-channel) signal between locations of source and destination. It might be possible that a certain type of special synchrony within a whole network is a possible solution, compare with Singer [SW93].
Interpretations of the effect of wave deletion reach from orthopaedics to acupuncture and kinesiology. In this fields amazing numbers of experiments are known where any sensitivity or excitement blocks a different sensitivity or excitement. The facit here: Silence is a good environment to be creative and powerful (in absence of deleting counter waves).
But there are further outstanding possibilities. Eccles [Ecc00], p. 254 remembered an experiment of Adrian and Matthews [AM34]. Using electro-encephalography they found, that any alpha-rythm of the brain (high amplitudes) can be suppressed completely by the opening of eyes. If we suppose, the frontal pulse waves input is higher with opened eyes, this higher rate suppresses probably the alpha-rythm of the brain by wave deletion effects. In other words: Is the average frequency reduced, the alpha-rythm allows, that informations reach cortical regions, that are much weaker or much further away - we seem to know this effect as "dream". Creative men also know, that we need silence to formulate a great, new idea - to reach farest regions of the brain.
In pain research, Mense [MS95] experimented with pain of rats. He found growing areas of medula spinalis produced by learned pain excitments. We know, that it is impossible to give commands for example to a broken leg. At one hand, pain produces cross-interference overflow, [NI93], Kap.5, S.104, see a simulation of the effect in [GH98], producing a non-locality of pain. At the other hand, the high frequency of pain waves deletes counter waves, prohibiting the sending of any information back to the painful organ (Fig.11).
Thanks to Andrew Packard for inspiring discussions in the specific field.
Gerd Heinz
[AM34] Adrian, E.D. and Matthews, B.H.C. Brain 57, pp.355, 1934
[APgl] The "Packard Glacier" in Antarctica was named for Andrew Packard. 1957/1958 he found first living organisms in the ice auf the glacier.
[AP95] Packard, A.: Organization of cephalopod chromatophore systems: a neuromuscular image-generator. In: Abbott, N.J., Williamson, R., Maddock, L., Cephalopod Neurobiology, Oxford University Press, 1995, pp.331-367
[AP01] Packard, A.: A 'neural' net that can be seen with the naked eye. In: Backhaus. W. (ed) 2001 International School of Biocybernetics (Ischia): Neuronal coding of perceptual systems: World Scientific, Singapore, New Jersey, London, Hong Kong. pp.397-402
[AP06] Packard, A.: Contribution to the whole (H). Can squids show us anything that we did not know already? Springer, Biology and Philosophy (2006) 21, pp.189-211
[AP11] Packard, A.: Squids old and young: Scale-free design for a simple billboard. Elsevier, Optics & Laser Techn., 43 (2011), pp.302-309
[AP23] After a fulfilling life in the service of science, Andrew Packard passed away on June 15, 2023 in his house in La Garde-Freinet (France).
[Bio96] Heinz, G., Höfs, S., Busch, C., Zöllner, M.: Time Pattern, Data Addressing, Coding, Projections and Topographic Maps between Multiple Connected Neural Fields - a Physical Approach to Neural Superimposition and Interference. http://www.gheinz.de/index.html BioNet'96, GFaI-Berlin, 1997, ISBN 3-00-001107-2, pp.45-57
[Ecc00] Eccles, J.C.: Das Gehirn des Menschen. Seehamer Verlag 2000
[GH94] Heinz, G.: Relativität elektrischer Impulsausbreitung als Schlüssel zur Informatik biologischer Systeme. 39. Internationales Wissenschaftliches Kolloqium an der TU Ilmenau 27.-30.9.1994, Abgedruckt in Band 2, S. 238-245
[GH96] Heinz, G.: Physikalisch orientierte Modelle von Nervennetzen - Hypothetische Modelle und Beispiele. Document only on the web, 1996
[GH98] Heinz, G.: Simulierter Schmerz als Überflutung aufgrund von Überfeuerung - Variation des Pulsabsstands einer dreikanaligen Pulsprojektion. Document only on the web, Sept.17, 1998
[GH01] Heinz, G.: An investigation of 'Pictures of Thought' - properties of pulsating, short circuit networks in Theory and simulation. Int. School of Biophysics "Neuronal Coding of Perceptual Systems", Cassamicciola, Isle of Ischia , Naples, Italy, Oct.12-17, 1998. Published in Backhaus, W.: Neuronal Coding of Perceptual Systems. Series on biophysics and biocybernetics, vol.9 - Biophysics, World Scientific, New Yersey, London, Singapore, Hong Kong, 2001, ISBN 981-02-4164-X, p.377-391
[GH04] Heinz, G.: Interference Networks - a Physical, Structural and Behavioural Approach to Nerve System. Lecture hold at "Brain Inspired Cognitive Systems" (BICS), 29 Aug. - 1 Sept. 2004, University of Stirling, Scotland, UK, on conference CD as #1115.pdf. Wave deletion played by refractoriness (Fig.11): Compare with [GH04] page 5, Fig.7b
[GH19] Heinz, G.: About a Holographic Brain and Non-Locatable Memory Contents. In Legacy of Karl Lashley, Donald Hebb, Lloyd Jeffress, Karl Pribram and Andrew Packard. Publication in WWW only, 2019.
[NI93] Heinz, G.: Neuronale Interferenzen (Pulsinterferenzen in Netzwerken mit verteilten Parametern). Autor gleich Herausgeber. GFaI Berlin, 1992, 1993, 1994, 1996, Persönlicher Verteiler in ca. 30 Exemplaren. 150...300 S.
[MS95] Mense, S.: Neuroplastizität und chronischer Schmerz. Uni Heidelberg, Publikationen, Ruperto Carola, Ausgabe 1/95, (Link)
[SW93] Singer, W.: Neuronal representations, assemblies and temporal coherence. In T.P. Hicks et all: Progress in Brain Research. vol. 95, Elsevier, 1993, Chapter 37, pp. 461-474
© Any commercial replication of this site or of parts of the site needs the written permission by the authors. Any non-commercial replication for education need a note with the name of the authors and the address (URL) of the source-file.
Mail to Andrew Packard:
andrew@packards.de
Mail to Gerd Heinz: info@gheinz.de
File created Nov. 24, 1998 gh/ap.
Revisions:
May 2005: text corrections. November 2020: Redesign; mpg-files converted to mp4; sources AP06, AP11, GH19 added; Fig.13 added, small textual corrections and adds, new layout. January 2022: Stylesheet included. July 2023: Obituary added; small additions; table of contents added.