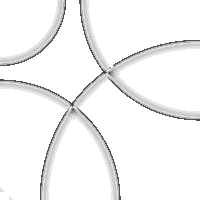back

Interferencial Projections in Distorted Space

The phantastic, acoustic 16-channel pictures of cars can demonstrate, what localisation capabilities an average, single neuron of our cortex with 7640 synapses must have. If a 'neuron' with 16 channels allows to recognize an excitement in a distance, that is 40-times greater the sensor arrangement, it is possible, that the smallest cortical neuron can feel any toe in a distance of kilometers - supposed the information is carried on different ways (axons)! A general new impression of neurocomputing appears, if we try to model delay properties simple accurate. In opposite to the here used reconstruction techniques with time inversion by right-hand masks, the neural system has to solve such attention tasks building the projection in real, non-inverted time. From simulation chapter we know, that projections with more then four channels produce the problem of over-conditioning in (homogenous) 3D-space:

space_dimension = channel_number - 1
or shorter:
d = k - 1

For example: We need k = 4 channels, to map into a 3d-space without over-conditioning.

We know from optical projections, that special arrangements with lenses exist, that solve the problem in ordinary 3D-space. To avoid over-conditioning in a more universal manner, we need a space dimension that is one order smaller the channel number. So projections onto 7640 synapses need a 7639-dimensional space (each dimension homogenous) to avoid over-conditioning. To construct such a space in general, the nature as we find only one solution: the delay space has to be inhomogenous to have the chance to give each synaptic sensor an accurate tuned delay. This seems to be only possible, when we create a 'fibre'-space!!! This idea was one of the introductionary impressions to try the 'Daumen-Versuch' (thumb-experiment, Dec.16, 1992) to find at the 'Relativity...'- pages.

Which interference effects occure, if we use an inhomogenuous, but continuous space, having a velocity function dependent of the location? To understand the things, we use a wave field reconstruction discussed in the simulation chapter. Normally it is supposed that the (delay-) distance dt between any location (x,y,z) and a channel source point (x0,y0,z0) is a linear function (velocity v) of the geometrical distance ds given by

dt = ds/v

with

ds = sqrt((x-x0)² + (y-y0)² + (z-z0)²) = sqrt(dx² + dy² + dz²)

We know, that a single neuron has very different dendritic and axonal diameters at different locations, thus signals have very different speeds within different parts of the trees. Also the neural tree is not expanding straight linear. Thus, the dependency between geometrical distance ds and delay-distance dt can be seen non-linear. Because the possibility to solve large neural networks in time domain numerically is not even realistic in the moment, it is suggested, that any (deterministic or stochastic) function f of the actual location modifies the delay distance dt in a non-linear, analytical matter.

f = f(x,y,z,x0,y0,z0), {f} = {-1...1}

dt = (f/F + 1) ds/v, {F} = {positiv, +1...+oo}

The quotient f/F we call distortion (in percent). For large F the influence of the term f/F disappeares. May be f is sinoidal periodic in dx and dy to get the following distorted fields.
The pictures give an impression, which effects occure, if we use inhomogenuous spaces to reconstruct interference projections. The same example is given several times as a wave field movie on different inhomogenuous delay spaces. The pictures may be seen as a part of an interference integral.
Note, that the interference events (waves meet eachother at special locations -> interference integral) appeare distorted in the same way.
Note also the possible encapsulation of waves in circles! This may be the only possible way, to interfere onto one neuron by a single channel (axon) in case, a neuron has some thousand synapses placed over a space greater the wavelength of incomming impulses.

Remark: PSI-Tools is only useable to simulate homogenuous fields.

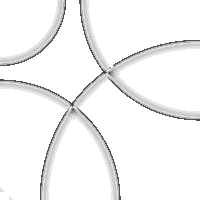
Four channel wave field (PSI-Tools simulation) projected in a homogenuous space (part of a wave field movie)


Same as above, but projected in a rippled, inhomogenuous space 5%


Same as above, but in inhomogenuous space 10%


Same as above, but in inhomogenuous space 15%. Note a new interference on a single location


Same as above, but in inhomogenuous space 20%


Same as above, but in inhomogenuous space 25%


Same as above, but in inhomogenuous space 30%


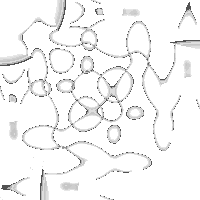
Same as above, but in inhomogenuous space 40%


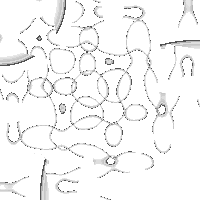
Same as above, but in inhomogenuous space 50%

Author

URL: http://www.gheinz.de/index.html

E-mail: info@gheinz.de

Sources

List of historical publications

Access No. since jan. 2, 1997