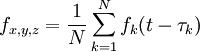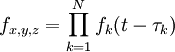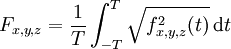nach oben

Versionsgeschichte:
Diesen Beitrag stellte ich Ende 2005 zusammen mit Beiträgen zu "Somatotopie" und "Akustische Kamera" auf Wikipedia. Leider wurden diese Beiträge 2006 ohne Rückfrage gelöscht. Erst als sie weg waren, konnte ich erfahren, warum, siehe folgender Screenshot. Vielleicht weiß man nicht, daß neue Theorien von niemandem - auch von keinem noch so gebildeten Professor - sogleich verstanden werden? Daß Publikationen in Fachjournalen zunächst genau so unmöglich sind, wie auf Wikipedia? Es sei denn, man hat einen "Förderer". Ein Teufelskreis.
Hier die Diskussion zur Löschung:

Merkwürdig, daß den Zensoren nicht auffiel, daß mit dieser "Privattheorie des Autors" die ersten akustischen Standbilder und Filme weltweit entstanden. Auch merkwürdig, daß die Herren wohl nicht die dutzenden Veröffentlichungen auf der Presseseite bemerkten (diese waren damals noch alle vorhanden - sie wurden erst nach Attacken von dubiosen Rechtsanwälten entfernt, Stichwort: mögliche Verletzung des Urheberrechts). Schade drum! Man fühlt sich an das Mittelalter erinnert.
Da fällt mir ein Witz ein: "Kennen Sie den Unterschied zwischen Kirche und Wissenschaft? - Ganz einfach: Es gibt keinen. Beide sind getragen vom Glauben!"


Interferenznetzwerk

(G. Heinz für Wikipedia, lokale Sicherung)

Wechseln zu: Navigation, Suche
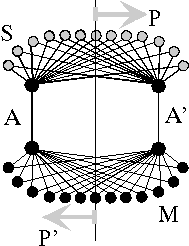
Wenn wir hinterfragen, was eine spiegelverkehrte, optische Abbildung mit einer spiegelverkehrten, nervlichen Abbildung (z.B. Homunculus) gemein hat, so nähern wir uns dem Gebiet der Interferenznetzwerke. Existieren übergreifende Prinzipien, die beide Abbildungen erklären? Lassen sich beide mit identischem Werkzeug berechnen? Gibt es eine übergreifende Theorie für alle Abbildungen selbst- und fremdinterferentieller Art (Seh- und Hörkarten)? Welche Zusammenhänge bestehen zwischen Welle und Wellenfeldintegral, dem 'Bild'? Sind dies Zusammenhänge, die nicht an eine Basis materieller Art gebunden sind? Existieren vielleicht sogar Wellenbeschreibungen, die ohne materielles Substrat auskommen? Was haben Andrew Packards beobachtete Farbwellen (siehe unten) mit nervlichen Projektionen gemein? Besitzt vielleicht sogar die Interferenz von Lichtwellen eine abstrahierbare Formelbasis signaltheoretischer Art? Dies sind Fragen, die von der Forschung auf dem Gebiet der Interferenznetzwerke zu beantworten sind.

Interferenzkreis nach Heinz, 1992
Einfachstes Interferenznetzwerk. Von P kommende Wellen treffen sich bei P' wieder - eine spiegelverkehrte Abbildung entsteht (Quelle: Heinz, NI, 1993)

Inhaltsverzeichnis

[Bearbeiten]

Überblick

Betrachten wir ein kreuz- und querverzweigtes Netzwerk, in welchem Zeitfunktionen sehr langsam dahinfließen (man stelle sich ein Nervennetz vor), so wird es Orte geben, an denen sich Wellen treffen. Berechnen wir an jedem Ort des Netzwerks den Effektivwert, und intergrieren über die Zeit, so werden sich die Treffer-Orte (wir wollen diese umgangssprachlich als Interferenzorte bezeichnen) nach einiger Zeit (im Interferenzintegral) energetisch abheben (siehe rot-violette Bereiche im Bild unten).

Quellorte und Interferenzorte stehen in Beziehung. Alle Abkömmlinge von einer Ur-Welle können sich im Netzwerk nur an Orten gleicher Laufzeit wiedertreffen (Selbstinterferenz, optische Analogie). Die Laufzeitgeometrie des Netzwerkes bestimmt dann dessen Funktion und Verhalten. Das Abbild einer Vorlage entsteht hierbei meist spiegelverkehrt.

Werden periodische Zeitfunktionen genutzt, so entstehen weitere Interferenzorte als sogenannte Fremdinterferenzen. Zusätzlich können sich hier Abkömmlinge eines Maximums mit folgenden Maxima oder mit Vorgänger-Maxima treffen. Frequenzkarten entstehen.

Mit dem Interferenznetzwerk entsteht eine Form der Signalverarbeitung, der selbst a-priori Kurzschlüsse (Kreuz- und Querverbindungen) im Netzwerk nichts anhaben können.

Interferenznetzwerke (Überlagerungsnetze) charakterisieren physikalische Wellenausbreitung in diskreten Netzwerken mit inhomogener, diskreter oder anisotroper Verzögerungszeitstruktur. In der klassischen Feldtheorie ist Wellenausbreitung im Wesen auf homogene und kontinuierliche Räume beschränkt. Betrachtet man eine eindimensional auf Leitbahnen wandernde Zeitfunktion als (eindimensionale) Welle, ist deren Ausbreitung durch ein kompliziertes, u.U. verwinkeltes Netzwerk (z.B. Nervennetz) zu hinterfragen.

Wir betreten das Gebiet der Wellenausbreitung in inhomogenen und diskontinuierlichen Räumen, das Gebiet der Interferenznetzwerke oder Interferenzsysteme. Dieses schließt die Berechenbarkeit auf homogenen und kontinuierlichen Räumen nicht aus. Während wir das Huygensche Doppelspaltexperiment mit den Mitteln der Feldtheorie nur stückweise lösen können, läßt es sich in einem Interferenzraum oder Interferenznetzwerk geschlossen lösen.

Die Begriffsbildung entspringt Untersuchungen zur mehrfachen Interferenz von Nervenimpulsen auf stark verschlungenen Leitbahnen. Interferenznetzwerke können zum Beispiel die Frage beantworten, wie ineinander kurzgeschlossene Nervennetze Informationen gezielt von einem Ort zu einem anderen übertragen können, siehe dazu auch Dermatom (Anatomie) und Somatotopie.

Das Potential nervlicher Strukturen wird über den Interferenzansatz erkennbar, wenn wir uns verdeutlichen, daß sämtliche Integraltransformationen der Mathematik als additive oder multiplikative Interferenzintegrale zweier Zeitfunktionen interpretierbar sind:

    • Fourier-Transformation
    • Laplace-Transformation
    • Z-Transformation (Discrete LT)
    • Wavelet-Transformation
    • Hilbert-Transformation
    • Gabor-Transformation
    • Auto Correlation
    • Cross Correlation
    • Convolution
    • Area Calculation (g=1)
    • Frequency Modulation (FM, PM, QM)
    • Amplitude Modulation (AM, SM)
Demgegenüber besitzt ein Pyrmidalneuron durchschnittlich 7400 Signaleingänge, kann also statt zweier 7400 Zeitfunktionen gleichzeitig miteinander verknüpfen.

Historie

Andrew Packard entdeckte 1995 Farbwellen auf Tintenfischen als sichtbare Erregungsweiterleitung nervlicher Art

Der Begriff des Interferenznetzwerkes wurde erstmals 1996 geprägt, als anläßlich eines Workshops in Berlin (Bionet96) herausgearbeitet werden konnte, daß künstlich-neuronale Netze (ANN) wesentliche Eigenschaften besitzen, die fundamental von natürlich-neuronalen Netzen (Nervennetz) abweichen. Die spezifisch notwendige Art einer verbesserten Modellierung wurde als Interferenznetzwerk bezeichnet: Hier ist jede Informationsübertragung an Verzögerungszeiten gebunden, Signale werden grundsätzlich als Zeitfunktionen modelliert. Verknüpfungen von Signalen sind demnach Verknüpfungen von Zeitfunktionen. Die zweidimensionale Variante von Zeitfunktionen aber bezeichnen wir als Wellen.
Die Entwicklung der Theorie neuronaler Netzwerke (Neural Networks, siehe neuronales Netz) stand 1943 durch einen Aufsatz von McCulloch und Pitts (siehe Andersen/Rosenfeld) an einem Scheideweg. Zeitfunktionen werden dort auf einer ganzzahligen Zeitachse miteinander verknüpft. Leitbahnen werden als elektrische Knoten betrachtet. Die Autoren schreiben Zeitfunktionen in der Form f(t - 1) oder f(t - 2) etc., man impliziert ganzzahlige Zustände. Durch logische Gatter oder Verzögerungsglieder werden die Zeitfunktionen oder Zustände verändert. Daraus entstand die Digitaltechnik, ohne die unser PC, die digitale Tontechnik, die Fuzzy-Logik oder die digitale Signalverarbeitung undenkbar wäre. Diese Sichtweise dominierte in Folgejahren auch die Forschung zu neuronalen Netzwerken in allen Bereichen.
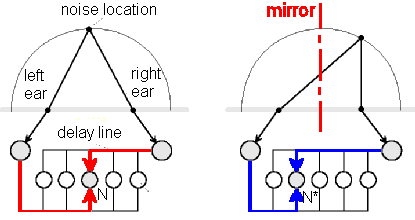
Unabhängig davon stellte Jeffress 1948 ein erstes Interferenzmodell eines nervlichen Netzwerkes vor, welches zwei gegeneinander auf Leitbahnen fließende Zeitfunktionen betrachtet. Jeffress Leitbahnen haben die Funktion von Laufzeitleitungen. Durch die präzise Laufzeitmodellierung entstehen völlig neue Eigenschaften: das Netzwerk kartiert spiegelverkehrt. Eine Schallquelle von links wird rechts im Gehirn abgebildet, eine Schallquelle von rechts wird links im Gehirn abgebildet.
Dieses Herangehen wurde lange vernachlässigt, die digitale Welt der Logik (Boolesche Algebra) und Zustandsmaschinen (Finite-State-Machines) prägte vierzig Jahre lang auch die Welt der Forschungen zu Nervennetzen. 1993 entstand eine weitergehende Untersuchung zu Eigenschaften von Netzwerken mit verteilten Laufzeitleitungen unter dem Titel Neuronale Interferenzen, siehe Weblinks. Dabei kamen interessante, neue Eigenschaften zum Vorschein. Da immer wieder Verwechslungen mit künstlich-neuronalen Netzen auftraten, werden diese Netzwerke seit einigen Jahren als Interferenznetzwerke bezeichnet.
Betrachten wir das langsame Kriechen von nadelscharfen Impulsen im Nervensystem, so ist dieser Ansatz für nervliche Modellierungen geeignet. Im Vergleich zur Zustandsbetrachtung (Pattern-Propagation) entstehen allerdings völlig andere Eigenschaften eines sonst identischen Netzwerkes. Dadurch setzt sich die neue Sichtweise nur sehr langsam durch.
Interferenznetzwerke schliessen die Modellierung von Leitbahnen mit unendlich hoher Geschwindigkeit (Knotenapproximation) sowie die Modellierung von Verzögerungselementen nicht aus. Entsprechend kann man künstliche, neuronale Netzwerke oder digitale Filter als spezifische Interferenznetzwerke mit diskretisierter Zeitstruktur ansehen.
Als einfachste Applikation entstanden mit einem zeitinversen Interferenznetzwerk der Form f(t+T) zwischen 1994 und 1996 erste akustische Bilder stehender Objekte sowie die ersten akustischen Filme, siehe Weblinks. Die Forschung zu Interferenznetzwerken begründete damit die akustische Photo- und Kinematographie.

Eigenschaften

  • Ein IN besteht aus signalverzögernden Kanten und signalverknüpfenden Knoten
  • Jede Informationsübertragung ist an endliche Verzögerungszeiten und Leitgeschwindigkeiten gebunden
  • Signale werden grundsätzlich als Zeitfunktionen modelliert
  • Verknüpfungen von Signalen sind Verknüpfungen von Zeitfunktionen
  • Endliche Leitgeschwindigkeit impliziert Zeitfunktionen als Wellen
  • Zwischen Zeitfunktion und Welle besteht Identität, die zweidimensionale Variante von Zeitfunktionen bezeichnen wir landläufig als Welle
  • IN besitzen inhomogene, diskrete oder anisotrope Verzögerungszeitstruktur
  • Insbesondere interessiert Wellenausbreitung in inhomogenen und diskontinuierlichen Räumen
[Bearbeiten]

Äquivalenz von Zeitfunktion und Welle

In Konishis Hörmodell von 1993 entsteht dieselbe Seitenvertauschung, wie bei einer optischen Linsenabbildung (Spiegelung)

Interferenznetzwerke beschreiben Interferenzen in meist höherdimensionalen Netzwerken, die durch komplizierte Laufzeit- Geometrien charakterisiert sind. Man versucht zum Beispiel, die Laufzeitgeometrie des Nervenraumes abzubilden, um neuronale Funktionen präzise modellieren zu können. Da experimentelle Daten aus dem Nervensystem nur mit höchstem Aufwand zu erlangen sind, bietet dieser Ansatz eine vergleichsweise einfache Möglichkeit, Funktionen des Nervensystems simulativ zu erkunden. Oft ist das Netzwerk-Modell durch Laufzeitmessungen und Anatomie bereits grob vorbestimmbar.
Dahinter steht, daß sowohl regelungstechnische oder logische Verknüpfungen von Zeitfunktionen, Differential- und Integralgleichungen als auch Wellengleichungen auf einen gemeinsamen, kleinsten Nenner gebracht werden können, der Multiplikation und Addition von Zeitfunktionen. Zeitfunktionen repräsentieren einerseits die Signalverknüpfung, andererseits besitzen sie Wellencharakter, sobald zeitliche Verschiebungen auftreten, siehe Interferenz.
Aus Betrachtungen zu Interferenznetzwerken geht eine spezifische Wellentheorie hervor, die von darunter liegenden Schwingungsproblemen weitgehend entkoppelt ist. Die Anwendbarkeit von Interferenzabbildungen auf Probleme in kontinuierlichen, wie in diskontinuierlichen Räumen (Netzwerken) erschließt eine spezifische Wellenbetrachtung: neben den von Wasseroberflächen bekannten Wellen entsteht ein Wellenbegriff für diskrete Netzwerke. Man stelle sich dazu zum Beispiel das wellenartige Fließen von Informationen in einem mikroelektronischen Schaltkreis oder in einem Nervennetz vor.
Interferenznetzwerke sind im Zeitbereich anschaulich darstellbar. Der Übergang in den Frequenzbereich verwischt einige Eigenschaften, wie z.B. die wesensbestimmende Unterscheidbarkeit zwischen Selbst- und Fremdinterferenz, wird aber nicht ausgeschlossen.
Räumliche Inhomogenität verhindert i.a. eine direkte Beziehung zwischen sphärischem Abstand und Verzögerung des Signals. Damit entsteht der Begriff der abstrakten Welle als spezifischer, verallgemeinerter Zeitfunktion, siehe Interferenz (Physik), Welle (Physik).

[Bearbeiten]

Einfachste Darstellung einer Welle

Räumlich sich ausbreitende, interferierende Zeitfunktionen sind Wellen (Film: Heinz, 1996)

Wie sieht ein Modell eines laufenden Pulses aus? Betrachtet man eine Zeitfunktion, so kann man diese üblicherweise als Abhängige von der Zeit f(t) beschreiben. Läuft diese Zeitfunktion nun von einem zu einem anderen Ort, so wird sie dabei um τ verzögert. Sie erhält im einfachsten Fall (Raum mit konstanter Ausbreitungsgeschwindigkeit v) die Form

f(t - τ) = f(t - ξ / v) = f(t*).

Treffen sich N Wellen k an einem Ort (Pixle x,y,z), so möge die resultierende Zeitfunktion fx,y,z aus einer Addition der einkommenden Zeitfunktionen entstehen:

f_{x,y,z} = \frac{1}{N} \sum_{k=1}^N f_k(t-\tau_k)

Division durch die Kanalzahl N liefert eine Normierung der Amplitude.

Für den Fall multiplikativer Verknüpfung setzen wir positive, auf den Bereich {0...1} normierte Zeitfunktionen voraus, hier wäre die Zeitfunktioon eines Pixels zum Beispiel

f_{x,y,z} = \prod_{k=1}^N f_k(t-\tau_k)

Das bewegte Wellenbild rechts entsteht zum Beispiel dadurch, dass für jedes Pixel der Bitmap eine Addition von vier Zeitfunktionen berechnet wird, wobei die jeweiligen Abstände vom Quellort der Welle die Verzögerungen τ = ξ / v bestimmen. Die unterliegende Wellenbeschreibung hat nur noch Zeit und Verzögerung als Parameter.
Damit wird eine Welle erkennbar als verallgemeinerte Zeitfunktion. Die Zeitfunktion stellt gleichzeitig eine abstrakte Welle dar. Die Welle wird zum Inbegriff von Zeit und entbindet sich jeder Materialität.
In Räumen mit isotroper Leitgeschwindigkeit liefert die Substitution τ = ξ / v (ξ als Betrag des räumlichen Abstands der Punkte) den Zusammenhang, der in Richtung dieses Spezialfalls der Wellengleichung führt.

[Bearbeiten]

Interferenzintegral

Interferenzintegral von vier Zeitfunktionen (Kanälen) als Projektion a) und als Rekonstruktion b) mit Zeitinversion gerechnet (Bilder: Heinz, 1996)

Beobachten wir viele Zeitfunktionen, die kreuz und quer durch ein (z.B. Nerven-) Netzwerk fließen und integrieren wir für jeden Ort (Bildpunkt oder Pixel) über eine gewisse Zeit, werden sich Orte, an denen sich viele Wellen treffen, im Effektivwert von Orten abheben, an denen sich nur wenige Wellen treffen.

Mathematisch integriert man für jeden Ortspunkt Fx,y,z über die Zeit, dabei entsteht ein Interferenzintegral zum Beispiel in der Form

F_{x,y,z} = \frac{1}{T} \int_{-T}^{T} \sqrt{f_{x,y,z}^2 (t)} \, \mathrm{d}t

wobei die auf den Ort i einströmenden Zeitfunktionen (Wellen) fk zum Beispiel additiv oder multiplikativ überlagert sind

In Analogie zur optischen Projektion entsteht bei diesem Vorgehen ein Bild als Interferenzprojektion, siehe Bild a). Wie in der Optik, zeigt sich die Projektion spiegelbildlich. Es fanden vier Kanäle Anwendung bei einer Raumdimension von zwei. Die resultierende Überbestimmtheit führt zu achsferner Unschärfe.
Interessiert für technische Belange ein Bild aus einem Wellenraum, welches die Quellengeometrie des generierenden Raumes unverzerrt wiedergibt (Sonographie, akustische Kamera etc.) so kann eine zeitlich inverse Rekonstruktion angewandt werden, die in den Quellraum zurückführt, siehe Bild b).

Die Bilder a) und b) entstanden aus vier Zeitfunktionen, die von den Ecken her in das Bild einströmen. Sie unterscheiden sich nur durch zeitliche Negation aller vier Kanäle (Zeitfunktionen).

Projektion (engl. beamforming; optische Abbildung, Ultraschall) und Rekonstruktion (nur in Software) sind zu unterscheiden. Die Interferenz-Projektion läuft zeitlich kontinuierlich voran, sie ergibt ein spiegelverkehrtes Abbild, welches nur in Achsnähe scharf ist. Dagegen läuft das Wellenfeld der Interferenzrekonstruktion in der Zeit scheinbar rückwärts, sie liefert ein seitenrichtiges Abbild und "belichtet" überall scharf.
Hintergrund für die achsnahe Schärfe ist eine mittels I.-Projektion nicht perfekt lösbare Abbildungsgleichung. Im Normalfall (akustische Kameras > 32) werden viel mehr Kanäle benutzt, als räumliche Dimensionen zur Verfügung stehen, wie bei einem dreibeinigen Hocker definieren drei Wellen einen Punkt auf einer zweidimensionalen Ebene n = d + 1 (Kanalzahl n, Raumdimension d), entsprechend definieren 4 Kanäle einen Ort im dreidimensionalen Raum (-> GPS), n Kanäle bilden dann aber nur im (n-1)- dimensionalen Raum ohne Überbestimmtheit ab.
Erst die Entdeckung der Interferenzrekonstruktion, die dieses Überbestimmtheitsproblem nicht hat, führte zur akustischen Kamera, siehe Weblinks.

[Bearbeiten]

Selbst- und Fremdinterferenz

Aus einer Untersuchung der Interferenz von Zeitfunktionen im Zeitbereich folgt eine für das Verständnis von Interferenznetzwerken wesentliche Unterscheidung.
Betrachten wir sich wiedertreffende Wellen in einem Raum (Linsenabbildung, akustische Kamera, Nervennetz etc.), so unterscheiden wir zwei wesensverschiedene Typen von Interferenz:

  • Dort, wo sich eine Welle mit sich selbst wiedertrifft, sprechen wir von Selbstinterferenz. Zeitliche Integration (das Interferenzintegral) definiert das, was wir in der Optik als Abbildung oder Projektion bezeichnen.
  • Treffen hingegen Wellen an einem (anderen) Ort auf ihren Vorgänger oder Nachfolger, so sprechen wir von Fremdinterferenz. Fremdinterferenz ist z.B. für die Zerlegung von Licht mittels Prisma, für auditive Karten im Nervensystem oder für die Nebenmaxima im Huygenschen Doppelspaltexperiment verantwortlich.
Selbstinterferenz und Fremdinterferenz sind untrennbar verknüpft, sie kartieren nur an unterschiedlichen Orten. Durch geeignete Ausführung eines Systems läßt sich die eine oder die andere Komponente betonen. In der Optik zum Beispiel betont eine Linsenanordnung die Selbstinterferenzen, eine Prismen- Anordnung hingegen betont die Fremdinterferenzen. Siehe auch einen Überblick.

[Bearbeiten]

Gleichnis von Hören und Sehen

Mit dem Begriff des Interferenzintegrals verschmelzen die Begriffe Hören und Sehen: Eine akustischen Kamera hört eigentlich ein (Selbstinterferenz-) Bild, die Zeitfunktionen werden über Mikrophone zugeführt. Wird der Begriff des Hörens auf Fremdinterferenzen bezogen, so bilden über das Interferenzintegral verschiedene Geräusche oder Töne verschiedene auditive Karten aus, vgl. Übersicht.
Hingegen sehen unsere Augen dank der Tatsache, daß die spezielle Ausführung der Linsenanordnung die einkommenden Zeitfunktionen des Lichts auf der Retina in (spiegelverkehrte) über das Interferenz-Integral in eine bildhafte Interferenz-Projektion umwandelt.

[Bearbeiten]

Systemtheoretische Parallelen

Mit den Begriffsbildungen Interferenznetzwerk und diskrete Welle fließen Systemtheorie und Feldtheorie zusammen. Dadurch könnten mit dem Ansatz zukünftig bislang scheinbar wesensfremde Wissensgebiete mathematisch nahezu einheitlich beschrieben werden:

[Bearbeiten]

Zeitdiskrete IN

[Bearbeiten]

Spatiale IN

[Bearbeiten]

Temporale IN

[Bearbeiten]

Literatur

  • Jeffress, L.A.: A place theory of sound localization. Journ. Comparative Physiol. Psychol., 41, (1948), pp.35-39
  • Konishi, M.: Die Schallortung der Schleiereule. Spektrum der Wissenschaft, Juni 1993, S. 58 ff.
  • Packard, A.: Organization of cephalopod chromatophore systems: a neuromuscular image-generator. In: Abbott, N.J., Williamson, R., Maddock, L., Cephalopod Neurobiology, Oxford University Press, 1995, pp. 331-367, (Filme hier)
  • Neurocomputing Foundations of Research (1988) Edited by James A. Anderson and Edward Rosenfeld. MIT Press, Cambridge, Massachusetts
[Bearbeiten]

Weblinks

Von "http://de.wikipedia.org/wiki/Interferenznetzwerk"