back

german
Origin: PDF, german

Relativity of Electrical Pulse Propagation -
Key to the Informatics of Biological Systems

Since 1992 the effects of a very finite running speed of nervous impulses (of ionic origin) are systematically investigated with respect to possible, informatically relevant functions of different, neuronal arrangements. Under the condition of conduction velocities of biological systems in the range of 0.5 - 120 m/s, impulse widths arise in biological systems, whose geometrical length lies with an assumed impulse peak of a tenth millisecond approximately in the range of 50 µm - 12 mm. A linkage of pulse values from different sources is therefore by no means statically feasible. In addition to the presence of the pulses, their coincidence at the location of the interference is also necessary for the linkage. Consequently, it is reasonable to assume that locations of interference might have something to do with addressing principles of neuronal information.

Conduction velocity and spatial resolution

Although well known in medicine (classifications according to Erlanger/Gasser 1939 as well as Lloyd/Hunt 1943 [1]), the running velocity of neural impulses remained neglected by AI research for forty years. Apparently, the modeling of nervous properties with delay-free, electrical conduction paths led to this mishap. Idealized, electrical conductions disguise the fact that the function of a logical component is only given if the signal duration d is very large compared to system-immanent delay times T of the conduction pathways. But exactly this is not the case in biological systems, geometric pulse length and propagation times of the arrangement are in the same order of magnitude: d ≈ T. As will be shown, the resulting logic type has nothing in common with the static type known from computer technology.

Table 1: Selected conduction velocities and geometric width of a 0.1 ms pulse

Fiber diameter [µm]	Type according to Erlanger/ Gasser	Type according to Lloyd/Hunt	Conduction velocity [m/s]	Function and occurrence e.g.	Geometric width of a 0.1ms pulse [mm]
12-20	Aα	I	70...120	Supply of striated muscles	7...12
6...12	Aβ	II	30...70	Skin afferents for touch and pressure	3...7
3...6	Aγ	-	15...30	Motor supply to muscle spindles	1.5...3
2...5	Aδ	III	12...30	Skin afferents, pressure sensitivity	1,2...3
1...3	B	-	3...15	Symphatic, preganglionic	0.3...1.5
0,4...1,2	C	IV	0,5...2	Markless fibers, pain of skin	50...200µm

The function of a gate is no longer determined only by its logic type. Into the logic function additionally the location enters. Only in the place of an interference an output appears. The relevance of this statement becomes clear when looking at the table. It should be noted that especially the thinnest, markless (i.e. non-insulated) fibers cause very low conduction velocities. Fine fibers form the so-called felt of the nerve plexus. Assuming a pulse duration of 0.1ms corresponds to the steepest part of a peak.

Fig.1: Although neuron A and neuron B (AND types) may have an identical function, they do not respond in the same way to the same impulse assignments.

Jeffress delay model 1948

According to Konishi [2], during a research vacation at Caltech in 1948, Jeffress is said to have given a then unpublished model circuit with non-ideal fast conduction pathways, which from today's point of view reveals some essential elements of biology-relevant signal processing. It offers a starting point (not yet recognized) for the interpretation of stochastically interconnected networks. Starting from this delay model, basic theoretical references of biological informatics will be presented.

Let us assume that the sound source shown in the picture emits periodically short pulses. (In the Jeffress model sinusoidal time functions are considered, but these complicate the essence of the process to be discussed). Then both partial waves propagate in equal times by equal distances, assuming equal velocities. Consequently, the partial impulses meet in the neuronal space at different places, if the source changes its locality. The place of arrival of the partial impulses is decided only by the speed of their progress, the relativity of the propagation of the impulses.

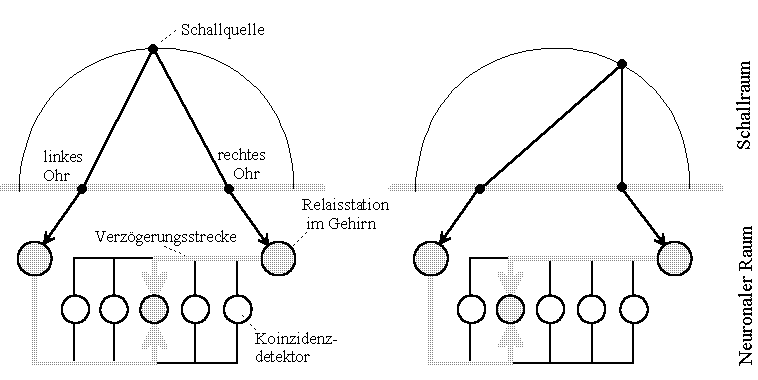
Fig.2: Noise location of a barn owl. Model Lloyd A. Jeffress according to Konishi [2]. The circuit model tries to explain how the brain can use travel time differences to locate a sound source. (Drawing freely according to source designated in the text)

The model illustrates that, given finite propagation velocity, differently positioned sound sources bring different coincidence detectors (neurons) to maximum excitation. All other detectors deliver weaker outputs the farther they are away from the location of interference.

In order not to have to use 'coincidence detectors' or other constructs which allow to compare correlating time functions, the concept of interference of time functions (waves) shall be introduced in analogy to physical-optical concepts. Two impulses or wave trains may be in interference at the place where the different wave components arrive simultaneously.

What remained unrecognized until today are the manifold properties, which can already be assigned to this simple model and which differ from the usual digital ones:

1. For the first time, a circuit model is given whose logical elements (neurons, coincidence detectors) perform non-deterministic tasks. For this purpose, imagine a source location interfering on the middle between two coincidence detectors. Sometimes more of the detector on the right is interfered with, sometimes more of the detector on the left is interfered with. Accordingly, both may work only once in a while. (This statement is highly explosive in so far as it makes the difference in principle between an interferential working principle and the well known working principles of digital logic circuits).
2. If the sound source as a template is shifted in the sound space by a piece dx to one side, its image in the neuron space wanders proportionally by another piece -dx' mirror-invertedly in the opposite direction. Obviously, template and resulting image are in proportion dx/dx' to each other. For linear systems this proportion is introduced as mapping scale M = dx/dx'. If it can be assumed that the template cannot consist of only one point (and this is given under certain restrictions), the template is homomorphically projected onto the image. Subsequently - borrowed from optics and mathematics - the term (neuronal) projection is used for such a connection.
3. The sharpness of the localization ds of an impulse is obviously related to the geometrical length λ of the impulse ds = k λ. The geometrical length λ in turn is related to the temporal impulse width dt with v = ds/dt = k λ/dt via the propagation velocity v.
4. The output of a neuron (seen as a coincidence detector) becomes dependent on the routing lengths of the input terminals. This behavior is spectacular in that in digital systems, attempts are made to strictly avoid exactly this in order to achieve conduction-independent or delay-independent functionality of the building blocks.
5. The logical consequence of the functional length dependence of the neurons is that the logical function is thus inevitably assigned to the location, but not to the linking element. In other words: already in this model it becomes recognizable that a nucleus magnocellularis, operationally displaced by a few centimeters, can no longer solve the same - i.e. no longer its actual task.
6. But if logical functionality becomes location-dependent, then the shell of a nerve structure encodes essential, functional properties of the same. Consequently, already the macroscopically visible, external form of a nerve structure influences its functionality.
7. Thus, the logical function is no longer assigned to the logical element, but to the location to which it is assigned. Under the condition of maximally interconnected elements, the logical signal flow is thus no longer controlled by the conduction paths, but by the transit times and position proportions of the space. Consequently, a stochastic, non-deterministic wiring can be chosen (within certain limits).
8. If it can be shown that runtime proportions change in a position-dependent manner, logical properties of neuronal elements will thus change in dependence on the momentary position or location of, for example, a body part.

Obviously, much more can be read from the model than known so far. Unnoticed, Jeffress has given a first interference model, on the basis of which already essential properties of neuronal (nerve-) networks can be derived, which are in stark contradiction to properties of known artificial neuronal systems.

(Later remark of the author: After my first publications about Interference Networks (IN), the until then so called "Neuronal" Networks (NN) were renamed into "Artifical Neuronal" Networks (ANN).)

Neural mapping in self-interference

Without knowing about Jeffress, the author developed circuits since 1992, which allow to simulate the transmission of mappings in stochastically interconnected networks.

Fig.3: Imaging interference circuit. A generator G feeds pulses simultaneously into both traces L at location x1. A multiplying receiver M (of AND-type) supplies an output only at the location of the interference x2. A pointer Z1 is thereby mapped to a pointer Z2.

If the transmitter G is moved along the x-direction, a multiplying receiver M must be moved in the opposite direction to get the possibility of receiving. Consequently, this is a circuit that projects, it is imaging.

If we extend this circuit principle, and place closely packed immobile neurons on the transmitting and on the receiving side, the same mapping occurs, if it is ensured that the different generator neurons pulse uncorrelated to each other. Also, the pulse density on the transmission lines must not exceed a certain level, to ensure that non-addressed neurons respond on the receiving side. We then see a circuit in front of us which is functionally as well as structurally exquisitely comparable to the nerve principle.

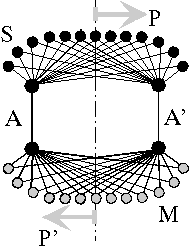
Fig.4: One-dimensional neuronal interference circuit (after Heinz [3]). For the transmission of an n-dimensional image, n+1 channels are required: pulse transmitter S, multiplier M, transmission channels A, A'; template P, image P'.

The circuit connects a location P of the transmitter side functionally and mirror-inverted with a location P' of the receiver side. Interference occurs at the place where the pulses running on different paths meet again, that is, where on the paths 1,2,...m equal propagation time between transmitter (t_a) and receiver (t_b) exists

The size of conjoined locations dx = kλ is proportional with a factor k to the geometric pulse width λ = vτ. If the place of interference is shifted by transit time changes of the guideways, other logic elements take over the task of previous ones. The mapping works cross-interference-free as long as the distance a = v(t_j - t_i) of two following pulses is larger than the length L of the field, v(t_j - t_i) > L.

Fig.5: Interference on a field with four feeding channels (snapshot).
a) Temporal relation of the incoming pulses
b) Determination of a possible interference location

Cross interference projections (general interference projections)

Besides the interference of an impulse with itself in self-interference, it is possible that an impulse enters into interference with some preceding or following impulse. This type may be called cross interference.

Fig.6: Neuronal diffraction as interference of different, periodic impulses with each other. The spacing between the maxima corresponds to the pulse numbers (j,k). (Lets call it "neuronal double-split experiment").

Adjacent maxima just have a difference s in the guide path length, which corresponds to the temporal distance Τ = (t_j - t_i) of two or more subsequent pulses

s = v (t_j - t_i) = vΤ.

Proportionality constant is the guiding velocity v. Correspondingly, for interference of two guiding pathways between source and interference location, in addition to self-interference, the following applies

τ_i + nΤ = τ_j + mΤ with (n,m) ∈ N

from which for k = n-m follows τ_j - τ_i = kΤ. For multiple transmissions the interference loci arise

τ₁ - a₁Τ = τ₂ - a₂Τ = ... = τ_n - a_nΤ with a_ν ∈ N.

Therein the solution for self-interference is included with a₁ ... a_n = 0 respective for Τ > τ_ν. Consequently, error-free mappings arise only with a weak channel occupancy! Overloaded channel assignments, e.g. for Τ < τ_ν can produce mapping errors (interference overflow, pain?).

Thumb experiment

(Later remark of the author: Innervated areas of single skin nerves have an extension up to several hundred square millimeters. In contrast, excitations can be perceived in the millimeter range. How is this possible?)

The electroencephalograph (EEG) is intended to detect multiple propagation and relative displacement of a wavefront with respect to the receiver. For this purpose, current pulses (peak 4mA, duration 1ms) are injected into the thumb (anatomical area of the radial and median nerves) with a pair of ring electrodes, which can be tapped above the wrist at points where these nerves come close to the surface using surface electrodes (see photo). The voltage waveforms of the median and radial nerves tapped at two pairs of electrodes are shown in the photo, radial nerve at the top, median nerve at the bottom.

When the position of the thumb is changed between the end positions, the position of the pulses changes with respect to each other. Two measurements are required for position variation. In a first measurement, the thumb is flexed outward. A relative delay time τ₁ between the taps for the meridian and radial nerve is determined. In the second experiment, the thumb is flexed inward. A smaller, and depending on the position of the taps relative to each other, even opposite in sign, relative delay time τ₂ is produced. During the experiment, the position of the electrodes must not be changed under any circumstances, and all electrodes must be carefully fixed to avoid slipping.

a) b)

Fig. 7: Measuring arrangement. The excitatory ring electrodes on the thumb and the conduction electrodes on the median and radial nerve can be seen. The wrist strap represents a grounding electrode to reduce 50Hz noise artifacts.

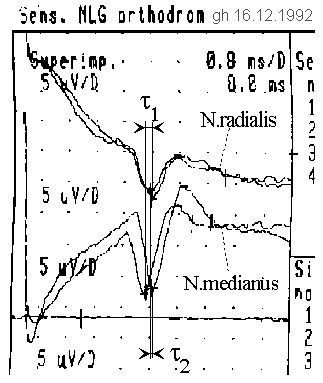
Fig. 8: Thumb experiment. If the thumb is fixed in different directions, different deceleration times can be measured relative to each other.

In the EMG-extract both measurements are superimposed to be able to compare the difference in the maximum accordingly clearly. Inadvertently, a result was printed in which, unnoticed in the experiment, a slightly different excitation current was set. This explains the deviations in the course of the median curves. Due to the relatively uncomplicated reproducibility of this experiment, the decision was easy to publish nevertheless the historically original, in the excitation of the hour exchanged originals of the first experiment on 16.12.1992, since they also reflect the essential result.

The impulses are fetched with an averager from the noise of random other impulses. After about 10 cycles, the imaged display quality is achieved. The shift can be seen particularly clearly at the median nerve (N. medianus). The larger bending radius in each case requires a longer run time. Due to the choice of the polarity of the electrodes, the pulse peak is downward. The pulses are about 1ms wide in the middle (plot: 0.8 ms/grid vertical, 5 µV/grid horizontal), whereas an unquantifiable offset of the averager causes an additional degradation of the pulse shape. It should be assumed that the actual pulse shape is much steeper.

Clearly can be seen, that the delay difference changes between the two diametral bending positions of the thumb. Outward flexion results in a delay of

τ₁ = τ_r - τ_m = -0.3ms,

inward flexion results in a delay of

τ₂ = τ'_r - τ'_m = +0.2ms

between the nerves N. radialis and N. medianus. In the hand sketch, wave fronts are symbolically drawn to illustrate the delays. The distance between excitation and tapping was about 13 cm, the average conduction velocity was v = 32.5 m/s.

The absolute time difference between the locations of two neurons x and y, which could potentially receive and evaluate the transit time differences differing from each other with maximum excitation, is

τ = τ₂ - τ₁ = 0.5ms.

Consequently, a difference in the length of the feeds to neurons receiving somewhere in the nerve system with maximum probability at arbitrarily assumed constant conduction velocity v = 32.5 m/s can be determined to be

s = v τ = 32.5 m/s * 0.5 ms = 16.25 mm.

If the natural pulse width is smaller than 0.5 ms (it is probably much smaller than that recorded by the averager), an excitation originating from the thumb will find different target addresses depending on the degree of diffraction.

Connection algorithm for interference mappings

A mapping between transmitter S and receiver M occurs at the point where the travel times of a pair of pulses across transmission lines A and A' are identical. It becomes clear that the algorithm for the design of connections is simpler than, for example, the laying of a house bell system of corresponding channel capacity. Connection algorithm for interference mapping (mono and bidirectional), see Fig.4:

• Lay out the transmission lines (A, A') true to coordinates;
• Connect each transmitter/receiver (S_i, M_j) to the nodes of the transmission lines by the shortest path.

Boundary conditions are, that locations to which transmitters or receivers are localized, are subject to strict timing constraints, and that transmitters pulse asynchronously with respect to each other. Interference between locations must be possible. Thus an envelope and body geometry is defined.

It becomes clear, that for the realization of an error-free pulse interference mapping not even a wiring plan (e.g. like an electrician uses for the installation of a house bell system) is necessary.

Summary

Studies on the relativity of neuronal pulse propagation and on interference phenomena of geometrically short pulses in neuronal networks reveal a causal binding of neuronal communication, addressing and storage to neuronal delay spaces. Biological, neuronal systems, observed here, are characterized by small pulse widths and slow conduction velocities.

The geometric pulse length is small relative to the dimensions of the system (body). The pulse length is measurable. The proof of this is possible with a conventional EEG- device. Biological systems are capable of learning, that means, due to a unknown target location before learning, impulses must be diffusely scattered into different pathways. If different nerve cells are connected to the impulse-carrying nerve pathways in different transit time geometries, the nerve cell, that is in the best possible interference with the transmission site, i.e. in which all partial impulses arrive simultaneously, is maximally excited.

Consequently, addressing of neuronal information considering diffuse impulse dispersion and diffuse wiring is given. A hypothetical calculation example illustrates this fact. Construction rules for interferential mappings are discussed. In the sense of genetic structure evolution, they are simpler, thus they are (DNA-) code simpler, than those of comparable "bell wiring models". Runtime effects, which appear as relativity of running times in neurons and on conduction pathways, represent the addressing procedure of neuronal information per se. Thus, delays (glia potential seen in EEG) can be used to control the size and location of the target area of information to be transmitted.

The investigation can be regarded as a proof that biological, neuronal systems cannot be modeled sufficiently by state machine modeling of the kind after McCulloch/Pitts under neglect of the running time and the geometrical length of neuronal impulses in the approach. In this respect, it becomes understandable that the great successes of artificial intelligence research have so far contributed little to the understanding of biological systems. A manuscript [3] produced with the research will appear in book form.

Acknowledgements

My sincere thanks to the EEG-specialist Dr. Torsten Griepentrog for his kind assistance in recording the EMG at the Landesklinik Teupitz (Land Brandenburg). Many thanks also to the head physician for psychiatry, Dr. Alfons Horn, for his kind consideration.

Literature

[1] Schmidt, R.F., Thews, G.: Physiology of Man, 24th ed., Springer-Verlag Berlin, 1990, p. 40

[2] Konishi, M.: The sound localization of the barn owl. Spektrum der Wissenschaft, June 1993 p.58-71

[3] Heinz, G.: Neuronale Interferenzen. GFaI-Report 23.12.1993 (300 p).

[4] Heinz, G.: Modeling Inherent Communication Principles of Biological Pulse Networks. SAMS 1994, Vol.15, No.1, Gordon & Breach Science Publ., Printed in the USA.

[5] Heinz, G.: Public lectures about neuronal interferences:
- GFaI/GMD-FIRST house 13.7, Akademiegelände Berlin- Adlershof, 27.8.93
- Fachhochschule für Technik und Wirtschaft Berlin-Karlshorst FB3 (Prof. Matschke), 28.5.93
- Public lecture at the Technische Fachhochschule Berlin-Wedding, Labor für Künstliche Intelligenz (Prof. Hamann),27.10.93
- Public lecture at the Institut für Mikroelektronik der Technischen Universität Berlin, 27.1.94

Autor

Dr. Heinz, GFaI e.V., Rudower Chaussee 5, Haus 13.7, 12484 Berlin,
Tel. +49-30-6392-1624, Fax -1602, e-mail heinz@gfai.fta-berlin.de

actualized:
e-mail info@gheinz.de
URL http://www.gheinz.de

Visitors since Dec. 2021:

Translation with DeepL-Translator www.deepl.com/translate