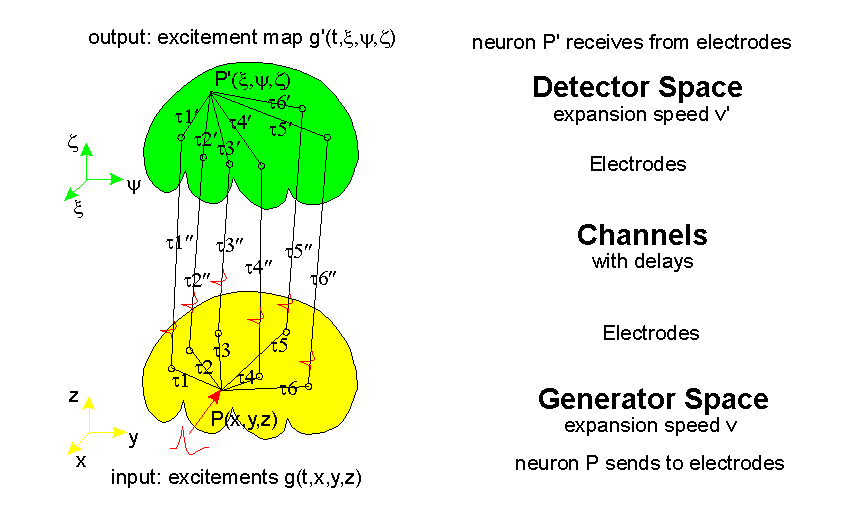
The page shows some first experiments with the interference transformation (IT). The IT changes time-functions to interference integrals. To get channel data, we use the inverse interference transformation (IIT) to get time-functions from an image. Also it demonstrates differences between projection and reconstruction at hand of some practical examples.
A projection appears as the natural way to project anything: A photograph, a sensitive map. The resulting interference integral field appears mirrored in general. Time flows straight forward. We compute the excitement at the destination field, the "detector space".

In opposite, reconstruction is the computational way to get the excitment map of the source "field" in nonmirrored form: by negation of the time axis we can calculate back into the source field, the "generator space". We compute back in time onto the generator-field. We get an approximation in form of a non-mirrored reconstruction.)
The terms "field" or "space" have only a demonstrative function. Each pixle of the "field" is connected direct to all channel origins, the delay of each line is proportional to its length. We come to a discrete, spherical wave propagation with this arrangement.
Supposed, we have neural activity at different places in a neural field (generator field). For example, spiking neurons are black pixels in the following bitmap in form of a 'G'. Supposed further, 30 sensors or electrodes connect this bitmap at "channel origins", numbers 0...29.
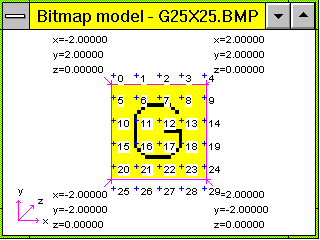
Neurons are supposed to fire synchronous in this example. For simplification, single spikes may have the following form:

Each discrete impulse-wave expands with 1 meter per second. In case of a circular expansion, the pulses reach the 30 different electrodes (0...29) at different times, if they come from different locations on the field. We suggest a homogenous (discrete) wave-space with delays proportional to the distance between the spiking neuron and the electrode.
If each "neuron" pulses once, we get following time-functions at thirty electrodes (channel origins 0...29). Using a small velocity, all black pixel pulseat the same time.

30 time-functions of a generator field with"GFaI"
The time-functions seem to look like EEG-samples or acoustic data streams.
Using PSI-Tools, we calculate the interference integrals for each generator-pixel (neuron) from the above channel data stream. The result is the following part of an *.avi-movie.

Wave field. Click the image to start a higher resolution movie (AVI)
We find the generating neuron's fire in the same moment. The reconstruction appears not perfect, the reconstruction quality appears proportional to a lot of parameters, like channel number, velocity, space distances, channel arrangements and delays. To examine the reconstruction parameters, inspect the INI-file used by PSI-Tools.
30 channels are located near the border. They got the time function waves from 57 pulsing pixels. Pulsing pixels were arranged in form of "GFaI". All pixels pulsed parallel. The reconstruction shows the following wave field, at least the waves meat at the locatikons of the 57 pixels. (To get a realistic impression, the movie seems to play time-inverted.)

Frozen view of last image

Click the movie for higher resolution (AVI, 680 kB)
For advertising purposes it is possible, to generate data streams also with other logos in a higher quality. It looks nice, to use a water bassin to interfere such waves. The channel data stream would be the same as used for PSI-Tools. We find the neurones fired synchronous (parallel).
Reconstruction for four channels with time inversion. This is the standard way, PSI-Tools produces interference images in reconstructive form. Pulsing neurons fired one by one onto four channels. These are the locations, where four waves meet. We find impanding waves of the so called pseudo-wave field. (It has no similarities with the original, generating wave field - only the approximatly equivalent interference integrals). Surprising, that the wave front is really inside the waves!

Click the movie for higher resolution (AVI, 247 kB)
The movie looks like a original wave field or a projection. Pulse waves come from channel source points, meeting at interference locations. But in this case it is produced using a time inverted timefunction of pulses as a reconstruction onto a detector field with reverse play of the movie - trick for the calculation of a detecting wave field of a projection. Terrible complicated - think about, draw images - it is the same thing!)

Four waves mark seven interference locations. Click the movie for higher resolution (ZIP 860kB, AVI 13MB)
For additive superimposition the amplitude at the excitment position will be n-times higher the amplitude of the single wave, where n is the channel number. The example gives an interesting view on the 'integrate and fire' principle in terms of spatial arrangements. Neurons are placed in form of the character 'G'. They fire at different times with a delay of approximately 0.5 ms. In the reconstruction we find the interferences really coming from single points. The excitement scale is the same over the images of the movie, we used 16 channels here.

16 time functions "channel data" of a generator bitmap "G" in serial fire

Wave field. Click the movie for higher resolution
Known from optics, over-conditioning problems of higher channel numbers restrict the image quality of projections. But using small numbers of channels, the possibility for phantom-excitement - these are cross-interferences within the image - grows! So the nature of our nervous system has to solve a dramatic conflict - find the best channel number for each signal connection between locations!
To remove cross interference we only can increase the delay between pulses. We include a pause between following pulses, while the channel remains still. The delay has to be greater the delay an impulse needs, to cross the detector field (field diagonale divided through speed), the resulting image appears perfect. We generate a four channel time function, the "electrodes" are at the corners.

Time functions of 4 channels, generated with a bitmap "GFaI"

Interference-integral of the 4-channel data set in 3D-view (PSI-Tools). Integration (over time axis) is necessarry, to get elementary wave-interferences appearing at different times into one excitment map.
File created sept. 30, 1995
Top http://www.gheinz.de/index.html
This page: Link
Mail to info@gheinz.de
Besucher auf www.gheinz.de seit 6. Dez. 2021:
All rights reserved, © Copyrights Gerd Heinz