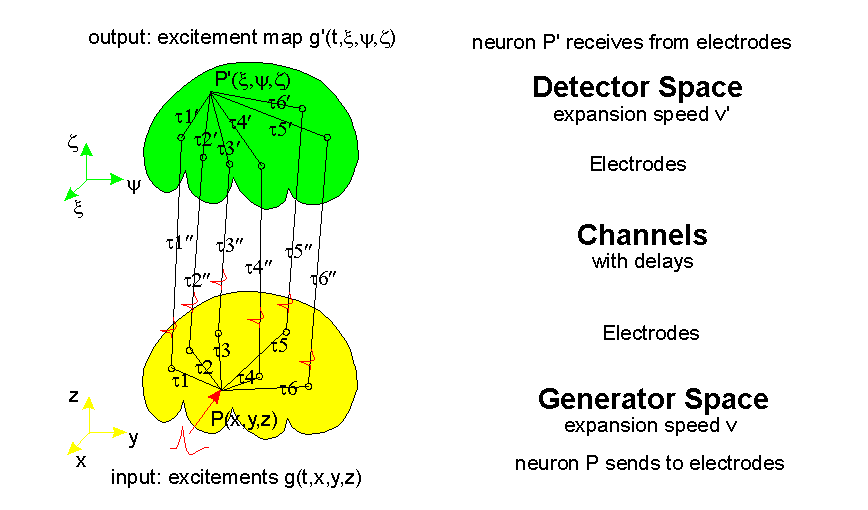
Die Interferenztransformation hat interessante Eigenschaften. Anhand der Wellenfelder sollen Wesensunterschiede zwischen interferentieller Projektion f(t-T) und -Rekonstruktion f(t+T) verdeutlicht werden. Dazu einige Beispiele.
Projektionen sind der natürliche Weg, etwas abzubilden, z.B. zu photographien. Dabei läuft die Zeit stetig voran. Mit einer einfachen Linse entsteht ein spiegelverkehrtes Bild der Vorlage: eine Projektion. Die Nachteile sind bekannt: nur entlang der optischen Achse entstehen scharfe Projektionen, der Rand eines Bildes erscheint kissenförmig verzerrt und unscharf. Je mehr Kanäle in die Projektion einbezogen werden, umso überbestimmter erscheint das Bild, umso stärker treten diese Effekte zutage.

Erst der Computer macht es möglich, die Zeitachse umzukehren. Aus der spiegelverkehrten Projektion wird eine seitenrichtige Rekonstruktion. Probleme wie Kissenverzerrungen und achsferne Unschärfe entfallen, da Überbestimmtheit entfällt (dies war die Grundidee für die akustische Kamera). Damit erst können wir beliebig große Öffnungswinkel der Kamera gestatten.
Dafür erhalten wir zwangsläufig rückwärts laufende Wellenfronten und rückwärts laufende Zeit bei der Generierung vorwärts laufender Movies(!) Während wir die Zeitrichtung bei Movies sogleich wieder invertieren können, bleiben die verkehrt herum laufenden Wellenfronten erhalten: sie sind ein untrügliches Kennzeichen der Rekonstruktion. Bei der Rekonstruktion entsteht ein von der Projektion verschiedenes Wellenfeld.
Wenn wir den Projektionsbegriff wählen, dann genau in der physikalischen Entsprechung zur optischen Projektion: im Gegensatz zum Begriff der mathematischen Projektion ist die physikalische Projektion spiegelverkehrt.
Im ersten Schritt wollen wir Kanaldaten aus Erregungen unterschiedlicher Orte generieren.
Angenommen, verschieden lokalisierte Neuronen in einem Nervenfeld feuern. Die spikenden Neuronen mögen als schwarze Pixel dargestellt werden, nicht feuernde Bereiche bleiben weiß. Folgende Bitmap enthält schwarze Pixel in Form eines 'G'. Dreißig Elektroden mögen diese Bitmap virtuell an verschiedenen Positionen kontaktieren, wir unterstellen der Bitmap dazu physikalische Dimensionen einer Ebene im Raum, mit denen PSI-Tools initialisiert wird. Jedes schwarze Pixel darf einen Puls erzeugen.
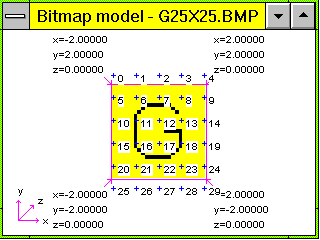
Das Generator-Modell des "G" mit 30 Elektroden (PSI-Tools) als Bitmap. Das "G" besteht aus 45 schwarzen (pulsenden) Pixeln.
Die Neuronen mögen zeitgleich feuern. Jeder einzelne Spike
soll folgende Form besitzen:

Verwendete Zeitfunktionen für die Spikes
Die einzelnen Impulse expandieren nun kugelförmig in einen homogen angenommenen (Laufzeit-) Raum. So erreicht jeder Impuls zu verschiedenen Zeiten die 30 verschiedenen, virtuell angeordneten Elektroden. Jede Elektrode addiert sämtliche Partialwellen aller Erregungen des Raumes, die durch eine endliche Ausbreitungsgeschwindigkeit unterschiedlich verzögert werden. Um die Dinge einfach zu machen, nehmen wir eine homogene Ausbreitungsgeschwindigkeit aller Wellen an. Die Verzögerungszeit, die eine Welle zwischen spikendem Neuron und abgreifender Elektrode benötigt, ist dann proportional dem Abstand.
Wir erhalten folgende Zeitfunktionen an den 30 Elektroden, jedes Elektrodenpotential bekommt eine andere Farbe.

Resultierende 30 Zeitfunktionen von 45 schwarzen Pixeln in Form eines "G"
Die entstehenden 30 Zeitfunktionen ähneln EEGs oder parallel aufgenommenen, akustischen Daten. Wir nennen den Übergang von räumlicher Anordnung zu zeitlicher Struktur der Kanaldaten inverse Interferenztransformation (IIT). Sie bildet das Gegenstück zur Interferenztransformation (IT), die Kanaldaten in Interferenzintegrale wandelt.
Nun wollen wir Wellenfeld mit den Interferenzorten der oben generierten Kanaldaten wieder rekonstruieren. Dazu benutzen wir die Interferenztransformation (IT). Während das Wellenfeld Schritt für Schritt zu bestimmen ist, berechnen wir die Interferenzorte als durchschnittlichen Interferenzwert für jedes Pixel des Ergebnisraumes (-feldes) über eine bestimmte Samplezahl. Diese richtet sich nach der untersten zu bestimmenden Grenzfrequenz des zu messenden Systems. Für jedes Filmbild wird das Interferenzintegral (I²) berechnet, es entsteht das folgende Movie:

30-Kanal 'G'-movie (AVI, 141kB)
Wir erkennen (nur unscharf), daß sich die einzelnen Wellen zeitlich rückwärts in die Elektroden hineinziehen (aus denen sie ursprünglich kamen). Auch erkennen wir, daß interferentielle Abbildungen nur Näherungslösungen sind: das "G" erscheint nicht perfekt.
Um die Bedingungen, unter denen diese Aufnahmen gerechnet wurden, zu erkunden, sehe man sich den PSI-Tools Ini-File an. Man vergleiche mit dem PSI-Help-File die Bedeutung der Variablen: Ini-file von PSI-Tools
Anhand vierkanaliger Aufnahmen können scharfe Wellenfronten synthetisiert und anschließend rekonstruiert werden. Der Grundgedanke von Interferenz im in sich tausendfach kurzgeschlossenen Nervenfilz wird offenbar: wenn mehrere Wellen gleichzeitig an einem Punkt eintreffen, wird dieser stärker erregt werden, als benachbarte Punkte.
Im ersten (niedrig aufgelösten) Movie sehen wir eine Rekonstruktion, wie sie PSI-Tools verläßt. Einwärts laufende Wellenzüge verraten die zeitlich invertierte Rekonstruktion. Die (leider verschwommenen) Pulsspitzen liegen im Innern der Welle!

Wellenfeld 'S'-movie (AVI, 247kB)
Es sind Interferenzorte aller vier Wellenzüge zu erkennen.
Aber auch Phantom-Dreifachinterferenzen sind zu sehen, die die Qualität
der Rekonstruktion verschlechtern. Dagegen hilft nur eine verlängerte
Pause zwischen den Pulsen, in der Neurologie als nervliche Refrakterität
bezeichnet.
Im zweiten, hochaufgelösten Movie haben wir die Bildfolge zusätzlich invertiert. Es scheint zeitlich vorwärts zu laufen, sogar die Pulsspitze liegt an der Wellenfront (siehe dazu ausführliche Erörterungen im Help-File von PSI-Tools).
Vorwärts laufende Wellen scheinen aber doch nur in der Projektion möglich zu sein: Irrtum. Das Movie ist nicht spiegelverkehrt! Folglich ist es keine Projektion. Die Pulsspitzen laufen den Wellen nur deshalb voran, weil auch zeitinvertierte Pulsformen bei der Synthese benutzt wurden. Es handelt sich um eine (zeitlich inverse) Rekonstruktion mit zeitlich invertierter Bildfolge und zusätzlich zeitinvertierten Pulsen! Soviel Trick muß sein, um eine qualitativ hochwertige Aufnahme eines zeitlich richtig an einem Ort interferierenden Wellenfeldes zu machen. Die Aufnahme entstand als populistische Demo für allgemeine Interferenz von Wellenfeldern. Es ist leicht zu erkennen, daß dieses Wellenfeld mit Projektion kaum herstellbar wäre: zu groß wären die achsfernen Überbestimmheiten, die zu einem unscharfen Rand führen würden.

'S'-movie (ZIP 900kB / AVI 13MB)
Bei sechzehn Kanälen ist die einzelne, zur Elektrode laufende Welle kaum noch erkennbar. Feuernde Neuronen sind wieder in Form eines 'G' angeordnet, siehe rechtes Bild. Hier feuern die einzelnen Pixel nacheinander. Wir können Interferenzen an einzelnen Punkten nacheinander beobachten. Man betrachte zum Vergleich die darunterliegenden Kanaldaten (Zeitfunktionen).

16-Kanal Wellenfeld des "G" (AVI, 41kB) mit Generatorfeld (rechts) aus 45 schwarzen Pixeln, die je einmal feuern dürfen

Aus dem Generatorfeld generierte Kanaldaten (K1...K16)
Zum Schluß wollen wir ein komplexeres Bild in Kanaldaten und diese wieder zurück zu einem Bild zu wandeln. Dazu wurde eine Bitmap mit den Buchstaben "GFaI" als Generatorfeld gewählt. Die vier aufnehmenden Kanäle sind in den Bildecken angeordnet. (Leider sind die Bitmap und der INI-File für PSI-Tools nicht mehr aufzufinden.)
Nervliche und optische Projektion stehen vor demselben Dilemma. Je höher die Kanalzahl gewählt wird, umso stärker ist die Abbildung überbestimmt, umso kleiner wird der mögliche Öffnungswinkel. Je geringer allerdings die Kanalzahl gewählt wird, je stärker steigt die Möglichkeit von Phantomerregung durch Fremdinterferenz. Während die Optik bei sinusförmigen Zeitfunktionen vergleichbar extrem hohe Kanalzahlen bei kleiner Öffnung benutzt, verwendet das Nervensystem geringe Kanalzahlen und spezielle, pulsförmige Zeitfunktionen, schon um Zooming und Moving zu ermöglichen.
Um das Problem von Phantomerregung in den Griff zu bekommen, erfand Gott offenbar die Refraktärzeit der Axonen. Die Refraktärzeit wird so groß gewählt, bis die Vorgängerwelle sicher über das Feld kommt, erst dann darf die nächste Welle erscheinen. Mit der zusätzlichen Idee steuerbar wegfallender Refrakterität löste der Herr gleich noch ein weiteres Problem: Wird die Pulsrate bei geringer Kanalzahl viel zu hoch, so nennen wir das vielleicht 'Schmerz'.
Doch Vorsicht: noch ist diese Auffassung weit entfernt vom biomedizinischen Mainstream, sie bringt einem immernoch unverdientes Gemurmel bei Konferenzen ein. Dennoch ist sie aber mit ein Papier, Bleistift und Taschenrechner oder mit PSI-Tools leicht nachzurechnen.

Aus dem Generatorfeld "GFaI" erzeugte Kanaldaten
Anhand dieser Zeitfunktionen ("Kanaldaten") wird klar, daß die einzelnen Interferenzen an verschiedenen Orten zu unterschiedlichen Zeiten stattfinden müssen. Wir benötigen eine Integration über die gesamte Zeitachse um die Emissionen aller Punkte zusammen zu erblicken - das Interferenzintegral. In disem Fall verbirgt sich hinter den 4 Zeitfunktionen eine Anordnung der Erregungspunkte in Form folgender Buchstaben:

Interferenzrekonstruktion der Kanaldaten in 3d-Darstellung
Werden die Pixel im Generatiorraum anders angeordnet, entstehen andere Kanaldaten. Im folgenden Beispiel wurden feuernde Pixel in Form der Buchstaben 'GFaI' angeordnet. Die einzelnen Pixel (57 Stück) feuern wiederum parallel, zu erkennen an der gleichzeitigen Interferenz aller Wellen im jeweiligen Zielgebiet. Zur scheinbar zeitrichtigen Wiedergabe (die Wellen laufen auswärts) wird ein Trick angewandt: Zusätzlich zu zeitinversen Kanaldaten wird die Bildfolge zeitlich invertiert. Man sieht die einzelnen Wellen aus den Quellen kommend zum GFaI-Symbol interferieren. (Anstelle der Pixel könnten wir auch 57 Lautsprecher anordnen.)
Eine Besonderheit dieser Aufnahme besteht darin, daß sie den gleitenden Übergang vom Wellenfeld zum Interferenzintegral sichtbar macht. Algorithmisch ist das Integral nur die Mittelwertbildung über die Wellen einer bestimmte Sample-Zahl pro Pixel.
Der INI-File war so gestaltet, daß eine recht geringe Leitgeschwindigkeit gewählt wurde. Damit konnten alle Pixel des Generators "GFaI" auf einmal feuern. Entsprechend finden sich in der zeitinvertierten Rekonstruktion auch wieder alle Wellen am Ursprungsort zusammen.
 Filmende eingefroren
Filmende eingefroren
 Film
Film
30-Kanal 'GFaI' Film (AVI, 680kB)
File created sept. 30, 1995
Top http://www.gheinz.de/index.html
This page: Link
Mail to info@gheinz.de
Besucher seit 6. Dez. 2021:
All rights reserved, © Copyrights Gerd Heinz