(back)
(english)

Heinz, G.: Neuronale Interferenzen.
Autor gleich Herausgeber. Persönlicher Verteiler, 1993, 301 S.

Neuronale Interferenzen


Inhaltsverzeichnis: (german), (english)

Anmerkungen zum Buch

Titelblatt

Informationen können nur dort miteinander verknüpft werden, wo sie zur selben Zeit anwesend sind. Diese Binsenweisheit zu verstehen, fällt offenbar nicht leicht. Und doch stellt sie den Schlüssel zum Verständnis von Interferenznetzwerken und zum Nervensystem dar.

Digitale Gatter im PC oder Smartphone setzen zum Beispiel voraus, daß die zu verknüpfenden Signale statisch für eine gewisse Zeit an den Eingängen eines Gatters anliegen. Computer besitzen deshalb Taktsignale und Taktfrequenzen. Der Zeitpunkt eines Takt-Übergangs von high auf low oder umgekehrt definiert die Übernahme von Daten in eine Baugruppe. Dazu muß das Taktsignal aber überall auf einem riesigen Schaltkreis (IC) auf Nanosekunden genau gleichzeitig vorhanden sein.

Während Drähte und Schaltkreise im Computer jedes Signal mit etwa einem Zehntel der Lichtgeschwindigkeit übertragen, sind Nervennetze rund eine Million mal langsamer. Dafür ist unser Cortex auch noch tausendmal größer. Cortikale Signale laufen so langsam, daß sie nicht zur Synchronisationion genutzt werden können: Die Informatik des Nervensystems ist nicht die eines Computers. Und als ob das nicht schon Horror genug wäre, sind nervliche Signale pulsartig. Neudeutsch sprechen wir von "Spikes". Und diese kriechen extrem langsam durch unser Gehirn. Wie also funktionieren Nervennetze?

Versuchen wir, zwei aus verschiedenen Richtungen kommende Spikes an einem AND-Gatter zusammenzubringen (hier die AND-Gatter A und B), so werden die im Bild nie gleichzeitig bei A ankommen: Aufgrund der asymmetrischen Verzögung durch τ wird der Ausgang von Gatter A still bleiben, nur der Ausgang von Gatter B wird reagieren. 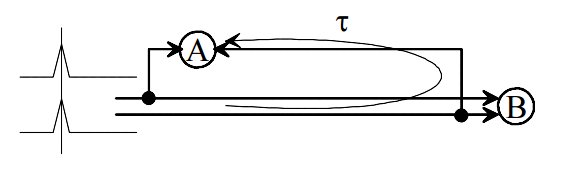Digitale Schaltungen funktionieren nicht so recht mit Spikes. Insbesondere dann nicht, wenn die Leitungen so langsam wie unsere Nerven sind. Informationen können nur dort verarbeitet werden, wo sie zur selben Zeit anwesend sind. Das läßt nur einen Schluß zu: Nervennetze funktionieren offenbar nicht so, wie unsere Computer. Wie aber funktionieren sie?

Um herauszufinden, wie Nervennetze funktionieren könnten, stellen wir uns vor, daß jeder Nerv in viele Richtungen verzweigt. Wenn wir jetzt zwei Spikes betrachten, die in unterschiedlichen Nerven herumirren, dann finden wir sicher eine Stelle, an der sie sich begegnen. Nur eine an dieser Stelle liegende Nervenzelle kann erregt werden.

Titelblatt

Im Gegensatz zum Computer, bei dem logische Pegel (0 oder 1) den Informationsgehalt bestimmen, bestimmt im Nervennetz der Ort der Gleichzeitigkeit des Zusammentreffens verschiedener Spikes eine Information. Nervennetze lassen sich damit nicht mit Computer-Informatik verstehen. Sie sind wesensverschieden. Wir haben es mit einer gänzlich verschiedenen Informatik zu tun.

Denkt man diesen Gedanken sehr lange weiter, entdeckt man das Prinzip dahinter: Nervennetze können nur projizierend (abbildend, bildartig) kommunizieren, niemals statisch wie ein Computer. Das erklärt, warum wir Jahre brauchen, um das Einmaleins zu lernen. Oder warum Gedächtniskünstler eine Bildergeschichte erfinden müssen, um sich ein paar Spielkarten merken zu können: Wir sind bei den Interferenznetzwerken angekommen. Der Informationsgehalt steckt wie bei einem Photo in der Schärfe einer Projektion. Aus Wellen werden Bilder und umgekehrt - Optik und Akustik fließen unter dem Dach der Interferenznetzwerke zusammen: "Sehend Hören" stand 1996 auf der ersten, akustischen Kamera.

Es grenzt an ein Wunder, daß der mit seinen Rattenexperimenten bekannt gewordene Karl Lashley ("In search of the engram") schon 1942 dazu kam, Interferenzen in Nervennetzen zu postulieren. Ich entdeckte folgendes Zitat leider erst im Nachlaß von Karl Pribram nach dessen Tod im Januar 2015. Karl hatte mir über die Jahre verschiedene Aufsätze zugesandt.

Donald Hebb schrieb in seinem Buch:

Dieser Ansatz wurde schnell zur universellen, aber für die Modellierung von Nervennetzen ungeeigneten Grundlage des Neuro-Computing (NN, ANN).

Warum aber meinte Lashley: "Hebb is correct in all his details but he's just oh so wrong"? Weil nur dort gelernt werden kann, wo die Verzögerungsstruktur des Netzwerks dafür sorgt, daß die zu verarbeitenden Informationen (Pulse) gleichzeitig ankommen. Wenn ein Neuron durch eine unpassende Verzögerungsstruktur die Partialpulse einer Quelle nicht gleichzeitig erhält, wird es weder lernen, noch etwas tun. Nur ein Neuron, dessen Verzögerungsstruktur eine Codedetektion (Kap. 10, S.210) ermöglicht, kann lernen oder etwas tun. Verzögerungen dominieren damit über Gewichte.

Der Autor bemerkte 1992 mit dem Daumenexperiment, daß Pulse in Verbindung mit sehr geringen Leitgeschwindigkeiten von Nerven eine andere Art von Kommunikation und Informationsverarbeitung hervorbringen. Die Verzögerung nadelscharfer Impulse bewirkt, daß nur dort Informationen verarbeitet werden können, wo Pulse sich treffen. Zeitliche Muster werden damit zu räumlichen Codes. Pulswellen breiten sich durch verschiedene Nervenfasern aus. Dort, wo eine Pulswelle mit sich selbst oder mit einer anderen interferiert, ist ihr Ziel erreicht. Oder dort, wo sich verschiedene Wellenfronten begegnen.

Um gedanklich weiter zu kommen, war eine Wellentheorie im Zeitbereich ebenso zu entwickeln, wie eine Wellentheorie auf diskreten und inhomogenen Räumen. Daraus entstand der Begriff 'Wave Interference Networks'. Im Manuskript sind Ideen auf dem Wege hin zu dieser unbekannten Informatik skizziert.

1992 war die Forschung zu "Neuronalen Netzwerken" (NN, heute als Artifical Neural Nets ~ ANN bezeichnet) an einem Tiefpunkt angelangt. Glaube und Fördermittel versiegten langsam. Techniker lehnten ANN zunehmend ab, weil deren Lernverhalten nicht verifizierbar war, den Biologen hingegen war der Zugang zu mystisch, siehe Zitat oben. Teils katastrophale Lernerfolge brachten das Aus. Übrig blieben ANN und als mathematisch/informatische Disziplin der sog. Konnektionismus. Zur Interpretation von Nervennetzen fehlte den NN etwas. Getaktete "Neuronale Netze" verletzen die Raumzeitstruktur eines zu modellierenden Nervennetzes grundlegend, dies führt zu katastrophalen Modellierungsfehlern bereits im Ansatz.

Digitale Filter nutzen die zeitliche Dimension, Netzwerke die räumliche. Im Nervennetz aber sind beide Dimensionen verbandelt: Je größer die Länge, je kleiner der Durchmesser eines Axon oder Dendriten, je größer der Abstand zweier Neurone, desto höher ist dessen Verzögerungszeit. Extrem langsame Leitgeschwindigkeiten sorgen zusammen mit pulsartigen Signalen dafür, daß Nervennetze im Gegensatz zu ANN ohne Takt auskommen müssen. Wie können solche Systeme funktionieren?

Nervliche Netzwerke stellen durchweg nicht synchronisierte Wettlaufschaltungen dar. Dort, wo sich ein Puls mit seinen Brüdern wiedertrifft, ist das Ziel erreicht. Das heißt: Allein die Verzögerungszeitstruktur des Netzes definiert Absender und Empfänger! Auf solchen Netzen lassen sich keine Bits addieren. Nur Bilder oder (bildliche) Zeichen sind übertragbar. Interferenznetze sind an Projektionen (optischer Art) gebunden. Und diese sind grundsätzlich spiegelverkehrt.

Auch werden im Buch auch n-dimensionale nervliche Filter besprochen, man denke an dreidimensionale, digitale FIR/IIR-Filter. Um Eigenschaften besser zu erkennen, erschien der aus der Optik bekannte Begriff der "Interferenz" als kleinster, gemeinsamer Nenner brauchbar. Informationen werden dort verarbeitet, wo Wellenberge in hoher, relativer Gleichzeitigkeit zusammentreffen. Folglich hießen diese Netze beim Autor ab 1996 "Interferenznetzwerke" (IN) (von "to interfere" - überlagern).

Schon 1992 war die Erkenntnis gereift, daß Pulsabbildungen nervlicher Art wenn überhaupt, dann nur spiegelverkehrt (siehe Titelblatt rechts) kartieren können. Als Adressierungsprinzip in neuronalen Räumen wurde mit dem Daumenexperiment die Relativität der Pulsausbreitung nachgewiesen, siehe im Kapitel 6 das Daumenexperiment vom 16.12.1992. Unbekannte Aspekte einer neuronalen Informatik fernab von Neuronalen Netzen oder Boolescher Algebra deuteten sich an.

Spiegelverkehrte Abbildungen waren in der Praxis aus Optik und aus Nervenexperimenten (Penfields Homunculus, Jeffress Schallortung) bekannt, nicht aber konnte man sie in der Literatur des Neurocomputing entdecken, die damals bereits hunderttausende Aufsätze und tausende Bücher umfasste. Systemtheoretisch stimmte etwas nicht mit den sogenannten "Neuronalen" Netzwerken. So begann diese Recherche.

Mit der Entdeckung der spiegelverkehrten Pulsabbildungen war es nötig geworden, die physikalisch realen Möglichkeiten dieser "Verzögerungsnetze", zu erkunden und deren Eigenheiten zu erkunden (Zooming, Movement, Interferenzüberlauf, Verbindung und Zerlegung, Überbestimmtheit, n-Dimensionalität, Raum-Zeit-Codierung, Nachbarschaftshemmung, Bursts etc.).

Diese Untersuchungen verliefen überaus erfolgreich. Sie führten innerhalb von vier Monaten zum Manuskript. So verschmelzen zum Beispiel "Sehen" und "Hören" über Untersuchungen zu Eigeninterferenzen (Seh-Karten) und zu Fremdinterferenzen (Hör-Karten) miteinander. Diese Erkenntnis bildete die Grundlage für die Entwicklung der ersten, akustischen Bilder und Filme zwischen 1995 und 1996 und der akustischen Bildgebung schlechthin für erste Akustische Kameras.

Eigentlich nur als Gedankenstütze gedacht, war es nötig, in kürzester Zeit die ungefähre Richtung eines Paradigmenwechsels von einer mathematischen hin zu einer physikalischen, wellentheoretischen Sicht auf nervliche Netze (Pulswellen auf Leitbahnen) zu skizzieren.

Interferenznetze können bei einer Vielfalt von Aufgaben, von der Optik über digitale Wettlaufschaltungen, Radar, Sonar, GPS, Beamforming, neuronale Netze bis hin zur Signalverarbeitung entdeckt werden. Digitale Schaltungen, Zustandsautomaten, digitale Filter, Pattern- oder Gewichtsnetze (künstlich-neuronale Netze) stellen aus dieser Sicht Untergruppen mit diskretem Timing dar. Nervennetze werden nur zum Synonym, um eine Vision einer abstrakteren Systemtheorie zu skizzieren, die der Interferenznetze. Die Vielfalt der betroffenen Wissensgebiete drängte förmlich auf eine theoretische Grundlage abstrakterer Natur. Ebenso wie digitale Filter sind Boolsche Algebren nur ein Untergebiet der Interferenznetze.

Im Buch sind einige Namensgebungen zu finden, die heute als unpassend gelten müssen. So hinterfragte Teuvo Kohonen** 1995 zum Beispiel die Verwendung des Begriffes "Faltung" (z.B. KA06.pdf, Seite 147). Hier stoßen wir auf eine Besonderheit von Interferenzsystemen, die möglicherweise ursächlich für den hürdenreichen Zugang ist.

Während die multiplikative, eindimensionale Interferenz zweier Impulse auf einer elektrischen Laufzeit-Leitung der mathematischen Faltung identisch ist (hier können wir die Zeitachse falten), verzichten wir im zwei- oder höherdimensionalen Raum auf den Begriff der Faltung vollständig, da sich hier keine Faltung der Zeitachse durchführen läßt. Hierfür wurde der "Maskenalgorithmus" eingeführt, der als Interferenzintegral auch das eindimensionale Faltungsintegral einschließt. Mehr noch: Schon für das eindimensionale Ischias-Nerv-Experiment mit Wellenauslöschung (Kapitel 6, S.144) versagen Faltungs-, wie Interferenzintegral.

Eine Abgrenzung zwischen Interferenzintegral und Faltungsintegral konnte 2011 in Bangkok vorgestellt werden. Eine Javascript-Rechentabelle wurde zum Thema Faltungsintegral versus Interferenzintegral entworfen, die die Dinge anschaulicher macht. Dort wird gezeigt, daß Faltungsintegral und Interferenzintegral (im eindimensionalen Raum) identisch sind. Einen Beweisansatz verdanken wir Alfred Fettweis, der die Identität von Interferenzintegral und Faltungsintegral für den eindimensionalen Fall herleiten konnte (siehe dort).

Greifen wir Zeitfunktionen zwischen generierendem Raum und detektierenden Raum als sog. Kanaldaten ab, entsteht die Frage der Berechenbarkeit der Bilder in beiden Räumen. Wollen wir den Generatorraum berechnen, sprechen wir von (seitenrichtiger) Rekonstruktion, soll der Detektorrraum berechnet werden, von (spiegelverkehrter) Projektion. Beide unterscheiden sich durch nur durch die Richtung der Zeitachse, bzw. die Richtung der Delays. PSI-Tools oder NoiseImage berechnen nur die Rekonstruktion, um damit auch Projektionen berechnen zu können, konnte bei PSI-Tools die Zeitachse invertiert werden.

Der Ansatz für Projektion und Rekonstruktion (als Grundlage z.B. der akustischen Photo- und Kinematographie) war mit diesem Buch gelegt, siehe Maskenalgorithmus, Kapitel 14, S.284. Mehr dazu siehe spiegelnde Interferenz-Projektionen vom Typ f(t-T), bzw. seitenrichtige Interferenz-Rekonstruktion vom Typ f(t+T).

Da Veröffentlichungen algorithmischer Art seit 1994 gegen kommerzielle Verwertbarkeit der Ergebnisse standen, z.B. gegen die der daraus entwickelten, ersten, akustischen Kamera, erfolgten diese nur spärlich.

Eine Kernaussage des Manuskripts lautet kurzgefaßt etwa: Nervennetze können nur mit einer dreidimensionalen, elektrischen Netzwerksimulation adäquat simuliert werden. Jeder Netzknoten benötigt Raumkoordinaten. Jeder Zweig benötigt eine Verzögerung (Delay). Alle aus der dreidimensionalen Struktur des Nervennetzes ablesbaren Delays sind genauestens abzubilden: Diese bilden wesentlich die Funktion aus ("Form kodiert Verhalten"). Daneben sind natürlich statische (anregende oder hemmende) Synapsen und Schwellwertparameter zu beachten. Wellenfront-Auslöschung auf bidirektionalen Zweigen ist genauestens zu modellieren.

Mit einer ersten Anwendung des gewonnenen Wissens für akustische Bildgebung zeigten sich bereits kurze Zeit später (1995) Erfolge: welterste akustische Bilder und Filme entstanden mit der Software "Bio-Interface", später umbenannt in "PSI-Tools" (Parallel and Serial Interference Tools, Sabine Höfs & Gerd Heinz).

Das Buchmanuskript wurde inklusive aller Formeln und Bilder mit Lotus Ami Pro unter Windows3.1 geschrieben. Ami Pro war wohl das effizienste Textverarbeitungsprogramm, das es je gab.

Formeleditor, Zeichenprogramm und Tabellen funktionierten innerhalb des Textprogramms, es war nicht nur das erste WYSIWYG-Programm (What You See Is What You Get), auch ließen sich damit Bücher schreiben. Man definierte Absatzformate (für Titel, Text, Bild, Formel etc.) und speicherte diese in einem *.sty-File (style sheet). Im Buch griff man von allen Kapiteln aus auf diesen File zu.

Leider funktionierte der Blocksatz nur bis zu Windows98 korrekt. Korrekturen konnten deshalb nur etwa bis zur Jahrtausendwende eingearbeitet werden. Die Datumsangabe im Einband war wohl auf 'File Creation Date' gesetzt.

Das Manuskript wurde aus eigenen Mitteln erstellt. Ohne Ami Pro wäre es nicht möglich gewesen, dieses Buch in so kurzer Zeit zu schreiben. Es musste im Mai 1993 beendet werden, da ab 1.6.1993 ein Job beim Arbeitgeber GFaI e.V. anstand. Kleinere Ergänzungen und Korrekturen folgten noch bis Anfang 1994 (z.B. der Abschnitt zur Schleiereule in Kap.1 "Jeffress Verzögerungsmodell 1948"). Mark Konishi hatte 1993 parallel zum Manuskript NI die Gedanken seines Lehrers Jeffres zur Hörortung publiziert***.

Das ursprüngliche Kapitel 10 (Interferenzlogik) war im Ansatz mißraten. Hier wurde eine mathematische Modellierung versucht, die sich als zu eng erwies. Das Kapitel wurde nach simulativen Verifikationen mit Peter Puschmann und Gunnar Schoel (FHTW 1994) später gegen das Kapitel "Elementarfunktionen des Neurons" ausgetauscht, siehe auch das originale Inhaltsverzeichnis von 1993. Im Index finden sich ebenfalls noch alte Verweise.

Das Buch stellte eigentlich ein Arbeitsmanuskript dar. Zusammenhänge und Ideen sollten nicht nur auf dem Skizzenblock notiert werden. Einschließlich aller Bilder und Formeln in einhundert Tagen geschrieben (Januar 1993 bis Mai 1993), ist es in Details unausgereift, Begriffsbildungen sind noch unsicher, es ist hin und wieder euphorisch, ohne daß der Leser dies immer nachvollziehen kann. Es zeigt anschaulich, in welchen Wirren sich ein neues Wissensgebiet entfaltet. Kurz: man vermißt die Rundung gereifter Werke. Dennoch erscheint es auch heute noch lesenswert. Viele generelle Erkenntnisse sind noch immer brandaktuell.

Um mit Thomas S. Kuhn* zu sprechen: Das Manuskript zeigt im Rückblick die Hürden des Weges, nicht aber den Glanz der Abstraktionen. Es ist eher für Wissenschaftshistoriker denn für Studenten geeignet. Dennoch: Es ist das Buch, dem wir akustische Bildgebung verdanken und dem wir allmählich eine Konsolidierung der Neuroforschung verdanken könnten: Wenn denn diese Grundlagen gelehrt werden würden.

Das Problem: Biologen und Mediziner haben nur eine rudimentäre Physik-, Informatik- und Mathematikausbildung; Physiker kennen weder Biologie noch Neuro-Anatomie. Das ist insofern betrüblich, als ein Verständnis vom Nervensystem erst dann möglich wird, wenn Neuroforscher beide Grundlagen beherrschen. Neuroforschung bleibt solange Stückwerk, solange Interferenznetze nicht vollständig verstanden werden. Einen Stahl schmiedet man auch nicht ohne Wissen über Feuer. Das sollte Fördermittelzuwendern bewußt werden.

Da bis heute noch kein richtiges Buch geschrieben ist (dazu wäre es wohl noch immer zu früh), mich aber immer wieder Bitten zu erklärenden Materialien zu Interferenznetzwerken erreichen, verbleibt dieses Arbeitsmanuskript solange im Web, solange nichts besseres vorhanden ist.

Manchmal ist der Weg das Ziel.


* Kuhn, Thomas Samuel: The Structure of Scientific Revolutions. Uni Chicago Press, 1962
** Kohonen, Teuvo: http://www.cis.hut.fi/research/som-research/teuvo.html
*** Konishi, Mark: Die Schallortung der Schleiereule. Spektrum der Wissenschaft, Juni 1993, S.58-71


© All rights reserved / alle Rechte bei Gerd K. Heinz, Berlin. Kommerzielle Verwertung benötigt die schriftliche Genehmigung des Autors.

http://www.gheinz.de
info@gheinz.de

Besucher seit dem 6. Dez. 2021: