Die mathematisch saubere Formulierung einfacher Wellenausbreitungen bereitet bereits Schwierigkeiten. In Fachbüchern finden wir teils gravierende Fehler. Zum Glück lassen sich die Gleichungen recht einfach simulieren. Hier Ergebnisse von Simulationen mit Scilab 3.1.1 (2006). Die Scilab-Quellen kann man sich ansehen, sie erscheint beim Anklicken des jeweiligen GIF-Movies.
Ein Wort zum Motiv dieser Wellensimulationen. Bei der Untersuchung von Zeitfunktionen aus dem Nervensystem stößt man auf zwei Aufgaben: die Rekonstruktion der Quellgebiete (des Generatorraumes) und der Projektion in die Zielgebiete (des Detektorraumes). Beide Aufgaben unterscheiden sich oft nur durch ein kleines Vorzeichen (a) <-> (b). Mir fiel auf, daß Vorzeichen von Wellen in Lehrbüchern oft wenig beachtet werden, zum Beispiel finden wir rückwärtslaufende Wellen bei Wikipedia:
http://en.wikipedia.org/wiki/Wave oder
http://de.wikipedia.org/wiki/Welle.
Man vergleiche die formale Identität der Scilab-Quellen und präge sich die richtigen und die falschen Formen ein.

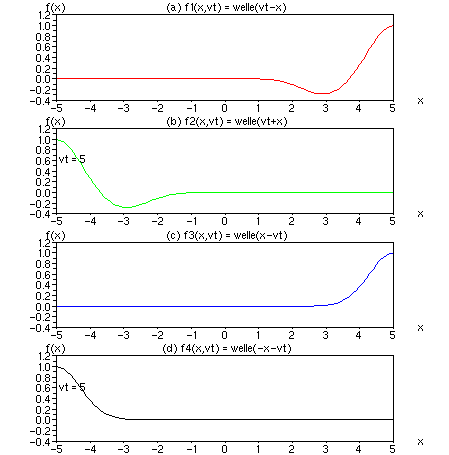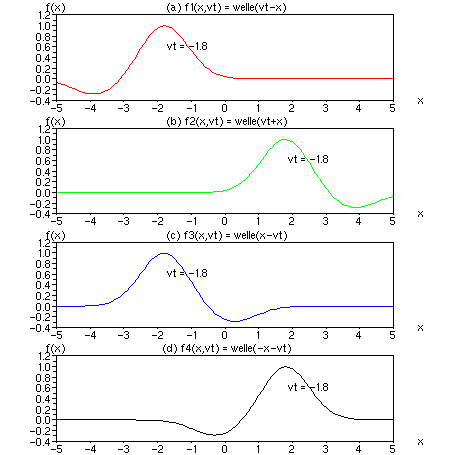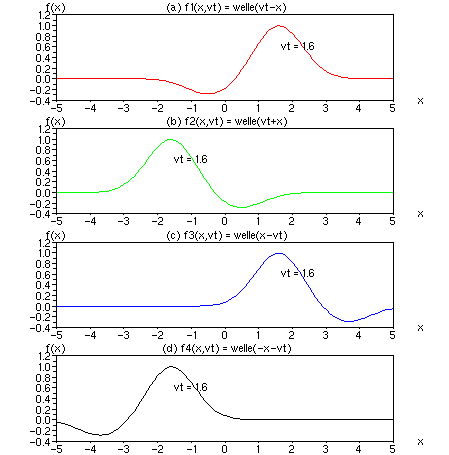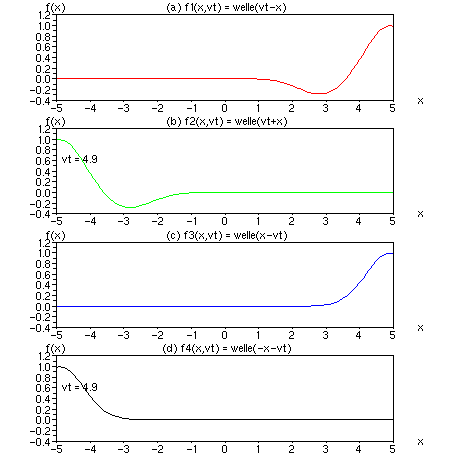
Bild 1: Animation zum Bild im Vorwort: Vier bewegte Ortswellen f(x,vt) einer Raumdimension. Ordinate: x, Abszisse: f(x). Der Schwanz der zugrunde liegenden welle(w) = gauss(w) - 0.3*gauss(w-2) hat im Kern den nachlaufenden Parameter (w-2), die minus 2 deutet auf einen zeitlichen oder örtlichen Nachlauf hin.
Diskussion: Mit den Vorzeichen von zwei freien Parametern x und vt lassen sich 2² = 4 Funktionen variieren. (a) und (b) zeigen Wellen, die nach unserem Empfinden vorwärts laufen. Dazu erhielten die Wellen einen kleinen Schweif. Im Gegensatz dazu laufen die Wellen (c) und (d) rückwärts, d.h. der Schweif läuft voran. Ist vt positiv, vgl. Nr. a) und b), läuft der Wellenberg voran. Ist vt negativ, vgl. Nr. c) und d), läuft das Wellental voran und der Berg hinterher.
Die mit dem Schwanz voranlaufenden Wellen begegneten uns gegen 1994 bei der Entwicklung des Rekonstruktionsalgorithmus von Bio-Interface (PSI-Tools) zum ersten mal. Noch fehlte die Phantasie, sich das zeitlich rückwärts laufende Wellenfeld vorzustellen, welches zu der rückwärtslaufenden Zeit in der Interferenz-Rekonstruktion gehört. Ich bat deshalb unsere damalige Softwareentwicklerin Sabine Höfs, das Interferenzintergral der Rekonstruktion eines (gesamten) Bildes in zeitliche Teilintegrale zu zerlegen. Überraschend erhielten wir die Wellenfelder mit rückwärts/ einwärts laufenden Wellen.
Die Fälle von Bild 1 (c) und (d) kann man theoretisch recht einfach korrigieren, indem man die obige, nachlaufende Wellenfunktion
welle(w) = waveM(w) = gauss(w) - .3*gauss(w-2)
durch eine Wellenfunktion ersetzt, deren Parameter (w+2) voraus läuft
waveP(w) = gauss(w) - .3*gauss(w+2).
Das Problem dabei: wird der Parameter w für die Zeit t benutzt
(w = t), dann haben wir es mit einem nicht-kausalen System zu tun, sofern wir natürliche Wellen simulieren, deren Parameter nicht in die Zukunft reichen dürfen oder können. Anders bei der rechnergestützten I.-Rekonstruktruktion, bei der eine Zeitumkehr bzw. nichtkausale, negative Delays genutzt werden.
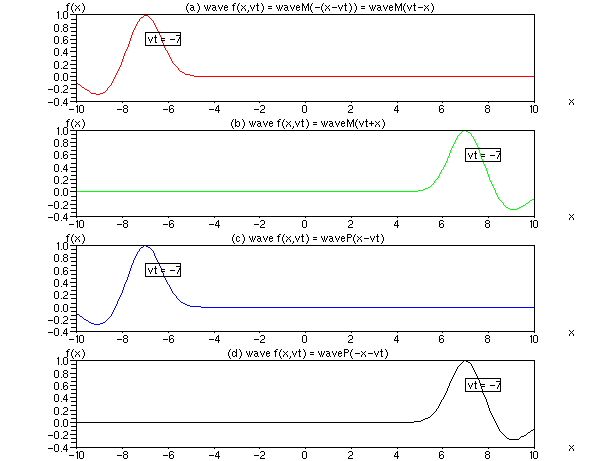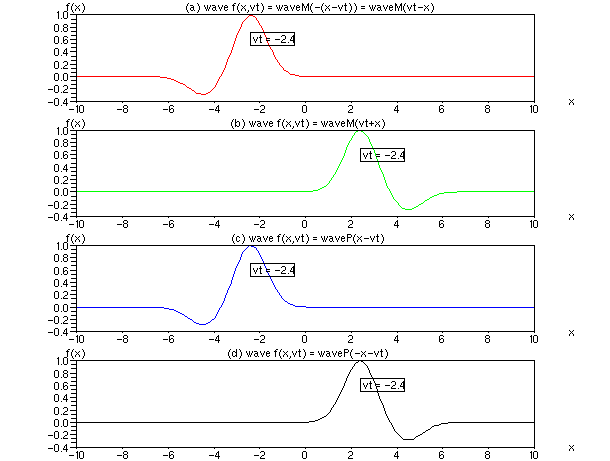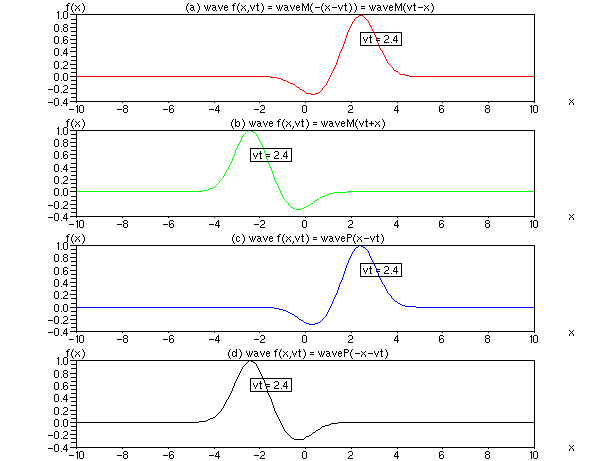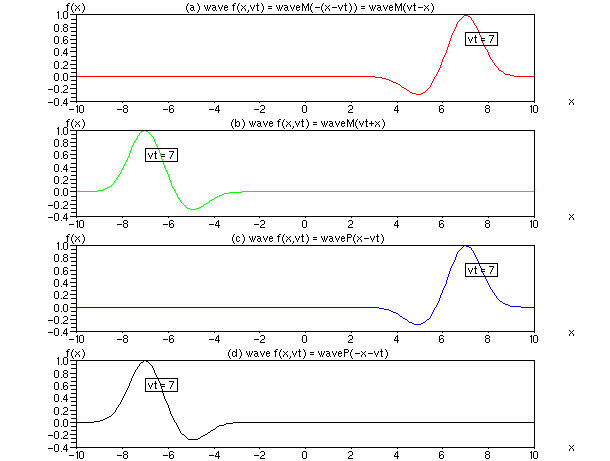
Bild 2: Nichtkausale Korrekturen für Bild 1 (c) und (d). Wird der Parameter für die Welle nach Bild 1, Fälle (c) und (d) welle = waveM (M wie minus) mit nachlaufenden Schweif durch welle = waveP (P wie plus) mit vorlaufenden Schweif ersetzt, scheinen auch die Formen von Bild 1 (c) und (d) richtig zu sein.
Ersetzten wir die Parameter x durch t gegeneinander, hätten wir ein Oszillogramm in Abhängigkeit vom Ort x vor uns.
Man vergleiche Bild 1 (a) bis (d) mit der eindimensionalen d'Alembertschen Wellengleichung: Wir erkennen Fall (b) und (c), statt (a) und (b). Die richtige Lösung der d'Alembertschen Wellengleichung sollte folglich im Kern vielleicht besser so aussehen:
u(t, x) = f(ct + x) + g(ct - x).Man vergleiche dazu auch deren Herleitung. Der Term x² = c²t² ließe sich nach c²t² -x² = 0 statt nach x² - c²t² = 0 umstellen: Schon entspräche alles unserer Anschauung, und die Wellen würden richtig herum laufen.
Die Darstellung von Wellen kann über die Zeit t oder über den Ort x interessant sein. Man vergleiche den Scilab-Code unter den Bildern. Ausgangspunkt bildet die Wellenform mit negativem Schweif nach Bild 1.
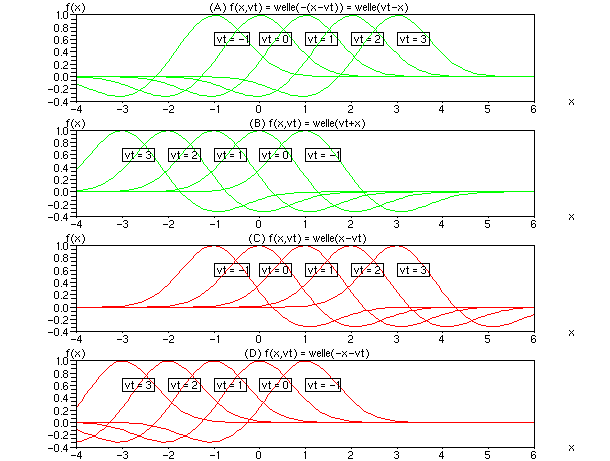
Bild 3: Die vier eindimensionalen Ortsfunktionen. Pro Kurve ist ein Zeitpunkt eingefroren. Denken wir an Meereswellen, kommen uns die grünen Wellen plausibel vor. Fälle (C) und (D) zeigen rückwärts laufende Wellen.
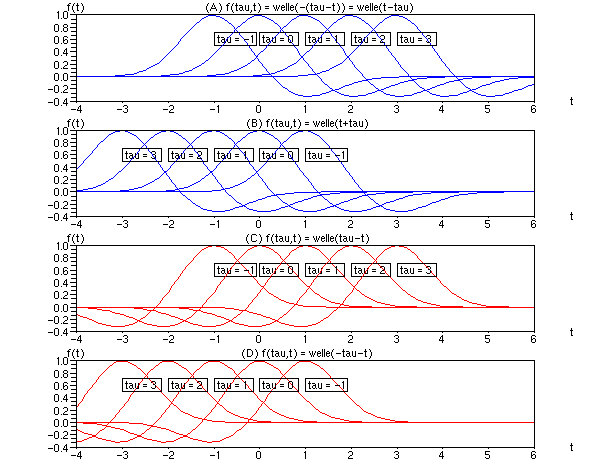
Bild 4: Die vier eindimensionalen Zeitfunktionen. Jede Kurve gilt nur für einen Ortspunkt. Denken wir an ein Oszilloskop, kommt uns diese Darstellung bekannt vor. Fall (A) zeigt wachsende Verzögerung, Fall (B) zeigt wachsende, negative Verzögerung, Fälle (C) und (D) sind eher unplausibel.
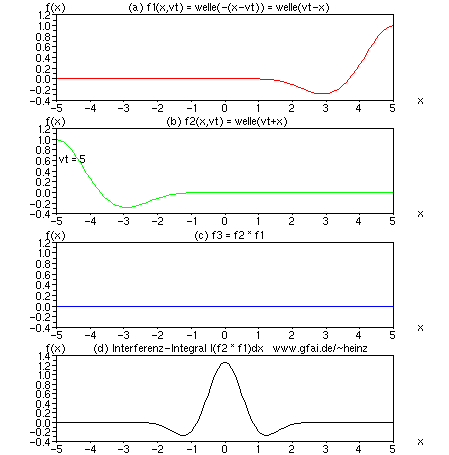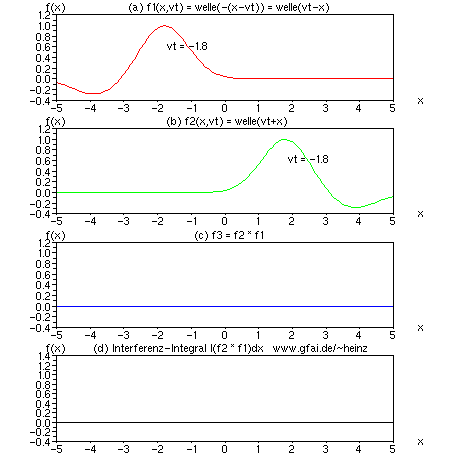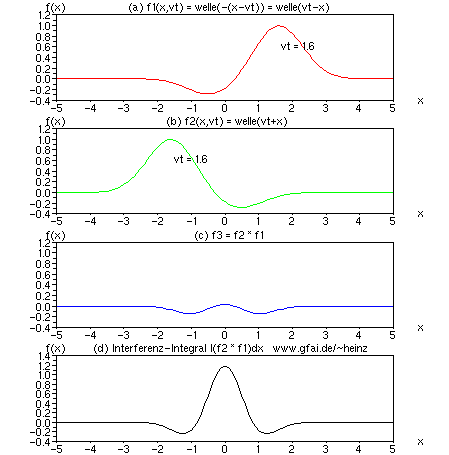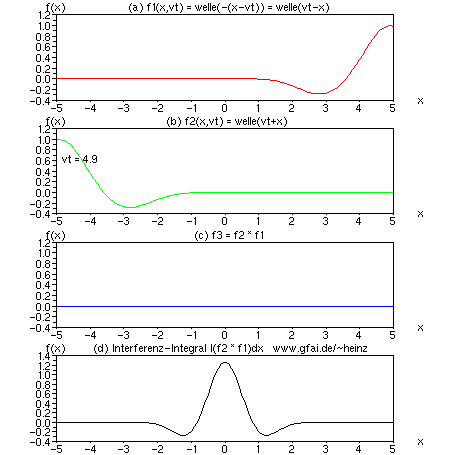
Bild 5: Interferenzintegral als mathematische Verbindung zwischen Welle (a,b) und Bild (d), zwischen Hören und Sehen. Dort, wo sich viele Wellen begegnen, entsteht eine hohe Wirkung (ein hoher Interferenzwert). Im Bild begegnen sich zwei Wellen. Den Ort der Begegnung zeigt bereits eine Multiplikation der Ortsfunktionen in (c) an. Um ein dauerhaft bleibendes Bild zu erhalten, integrieren wir den Wert für jedes Sample separat auf - ein Interferenzintegral (d) entsteht. Während (a) bis (c) Zeitfunktionen darstellen, zeigt das Interferenzintegral (d) die Entwicklung eines bestimmten Bildpunktes.
Ein Interferenzintegral stellt die elementarste Abstraktion der Bildentstehung auf dem Niveau von Zeitfunktionen dar. Wir erkennen, daß sinoidale Zeitfunktionen hier keine Rolle spielen müssen. Bestehen Zeitfunktionen aus Lichtquanten, spricht man von Photographie, sind sie mikrophonierter Schall, erhalten wir akustischen Bilder z.B. mit einem Ultraschallgerät oder mit einer akustischen Kamera aus vielen, parallel aufgezeichneten Tonspuren. Sind Zeitfunktionen neuronaler Natur, sprechen wir von Sehen, Hören, Fühlen oder Denken. Allerdings kann wohl nur des Nervensystem die multiplikative Form nutzen, da nur hier einpolare Signale anzutreffen sind. Optik und Akustik nutzen additive Formen, siehe folgende Beispiele. Man beachte die vielfältigen Wechselwirkungen zwischen Zeitfunktionstyp, Parametern, Verknüpfung und Integral.
Zu Bild 5: Es zeigen (a) und (b) interferierende Zeitfunktionen f1 und f2; (c) eine skalare Multiplikation beider Zeitfunktionen f3 = f1 * f2 und (d) ein zeitliches Integral über f3 in der Form f4 = f4 + f3; f4 ist initial Null. Die Variablen f1...f4 sind in der numerischen Durchführung Vektoren (eindimensionale Matrizen). Für jedes vt entstehen die Vektoren f1...f4 neu.
Der hier vorgestellte Ansatz ist nur für den eindimensionalen Raum und zwei Zeitfunktionen geeignet. Denkt man an mehrere Zeitfunktionen, die im Winkel aufeinander treffen, so wird deutlich, daß hier nur ein Spezialfall behandelt wird. Für mehr als zwei Kanäle in räumlichen Geometrien war ein anderer Denkansatz zu finden. Die Erfindung akustischer Bilder und Filme mit der später so bezeichneten akustischen Kamera basierte auf der heute so bezeichneten Interferenz-Rekonstruktion, die 1993 als Maskenalgorithmus eingeführt wurde.
Was passiert, wenn eine der beiden Wellen zeitlich verzögert ins Feld kommt? Im eindimensionalen Fall verschiebt sich der Treffort auf der x-Achse mittig. Im höherdimensionalen Raum würde sich der Ort der Interferenzen im Raum verschieben, siehe Movement. Analog dazu führt eine Veränderung der Leitgeschwindigkeit zum Zoom-Effekt, das Bild wird dabei vergrößert oder verkleinert.
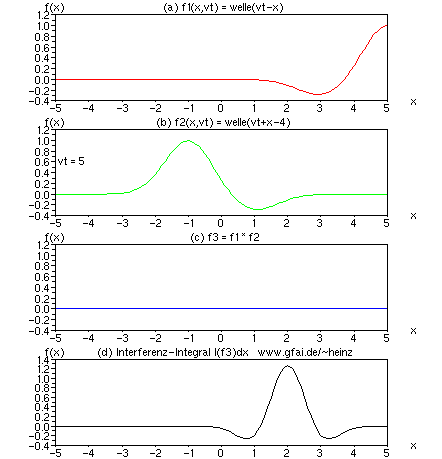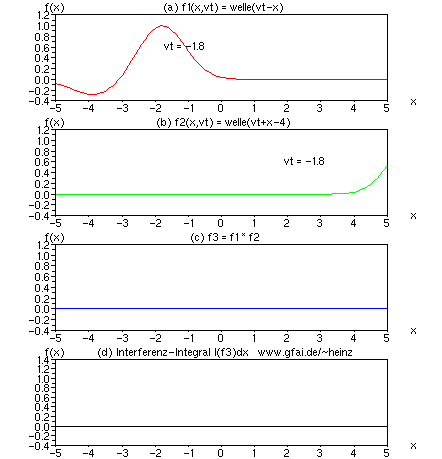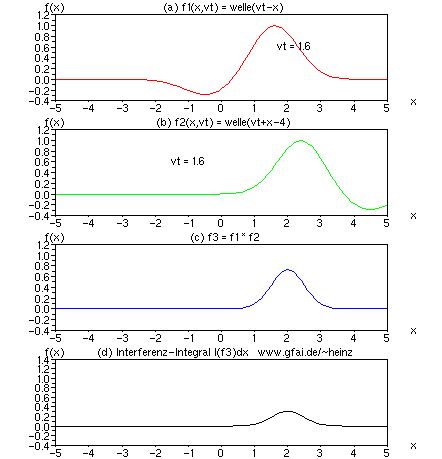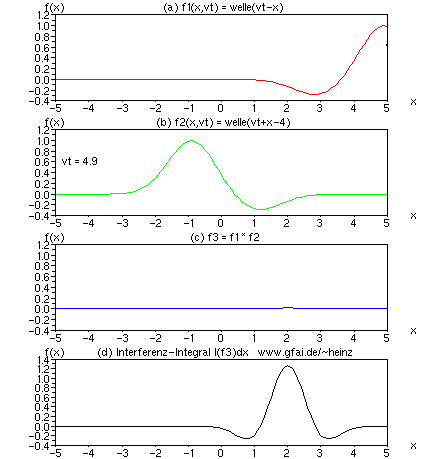
Bild 6: Im Bild wurde die zweite Welle (b) f2 = welle(vt + x + vT) verzögert um T = -4/v. Im Interferenzintegral (d) erkennen wir, daß sich der Treffort beider Wellen auf x = 2 verschiebt. Wir erkennen, daß zeitliche Verzögerungen in Zeitfunktionen zur Veränderung der Interferenzorte führen. Im Nervensystem bestimmen damit Verzögerungen den Ort der Verarbeitung eines Pulses. Das mag der wohl fundamentalste Unterschied zur gewöhnlichen Digitalschaltung und zum Computer sein!
Das Interferenzintegral verschiebt sich immer zur verzögerten Welle hin. Verzögern wir einen Kanal, so bewegt sich ein gesamtes Bild (vielleicht eine neuronale Karte) zur verzögerten Seite hin (siehe Movement): Interferenznetze zeigen damit eine Projektionseigenschaft, die wir aus der Optik kennen.
Wir bekommen eine Idee von der Aufgabe von Glia-Zellen, in die Nervenfasern eingebettet sind: Sie können die Leitgeschwindigkeit eines Nervs verändern, folglich ändern sie dessen Signalverzögerung, folglich verschieben sie Interferenzorte, folglich Interferenzintegrale und -karten. Und folglich steuern sie den Ort der Verarbeitung! Nach Auffassung des Autors sehen wir übrigens im EEG nur die Steuerpotentiale der Glia. Was das bedeutet, ist bislang unklar.
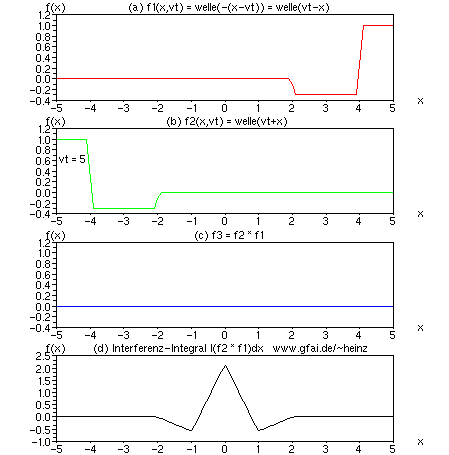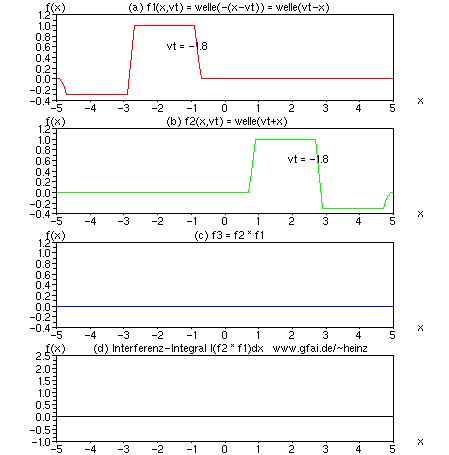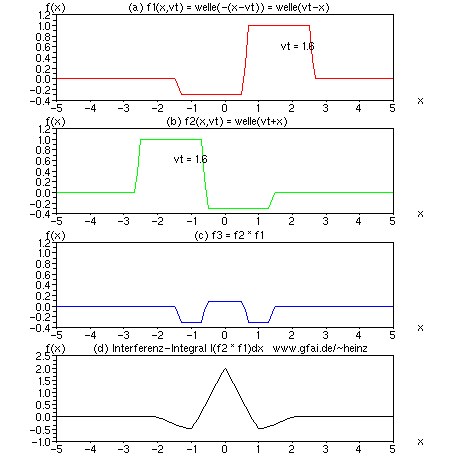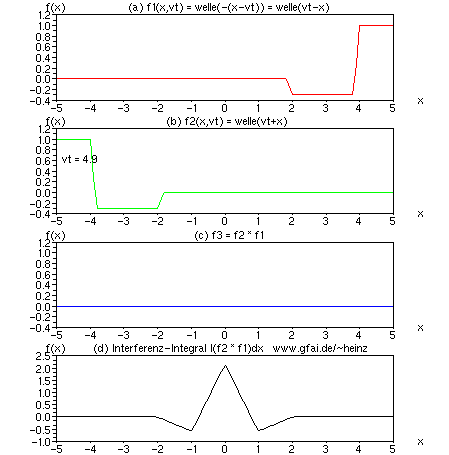
Bild 7: (a) und (b) Zeitfunktionen; (c) Momentanwert der Multiplikation; (d) Interferenzintegral. Man beachte, daß das Interferenzintegral (Wavelet-Analogie: Mallat) nadelscharf auf der x-Achse abbilden kann, obwohl die Zeitfunktionen (Wavelet-Analogie: Haar) erheblich klobig erscheinen.
In das Nervensystem übersetzt bedeutet diese Simulation, daß jegliche Schwellwertbildung (man vergleiche Neuronenmodelle zeitlich nach Hodgkins/Huxley) zu nadelscharfer Lokalität der neuronalen Adresse führt, auch bei vergleichsweise großer geometrischer Länge der Wellenplateaus.
In die Sprache bildgebender Systeme übersetzt, bedeutet es: Mit Interferenzintegralen ist es prinzipiell möglich, Auflösungen in Bruchteilen einer Wellenlänge zu erreichen. Da mediale Eindringtiefen i.a. in Vielfachen einer Wellenlänge gemessen werden, bedeutet der interferenzielle Zugang damit eine Erhöhung von Eindringtiefe oder Auflösung.
Diese grundlegende Entdeckung veranlasste mich 1993 u.a., mit dem Manuskript Neuronale Interferenzen zu beginnen. Als Beispielapplikation entstanden bis 1997 erste, akustische Bilder und Filme. Die Geburtsstunde der akustischen Photo- und Kinematographie war gekommen.
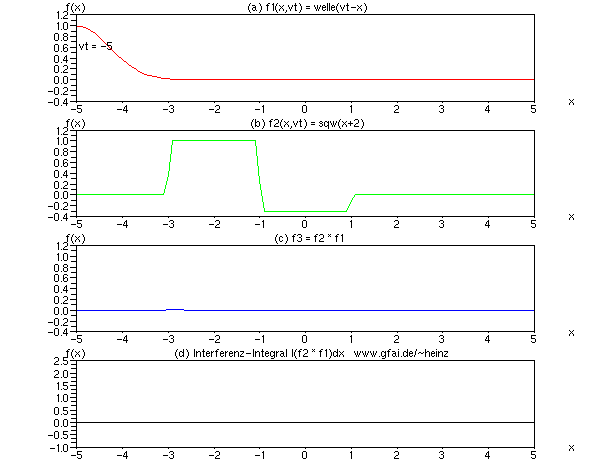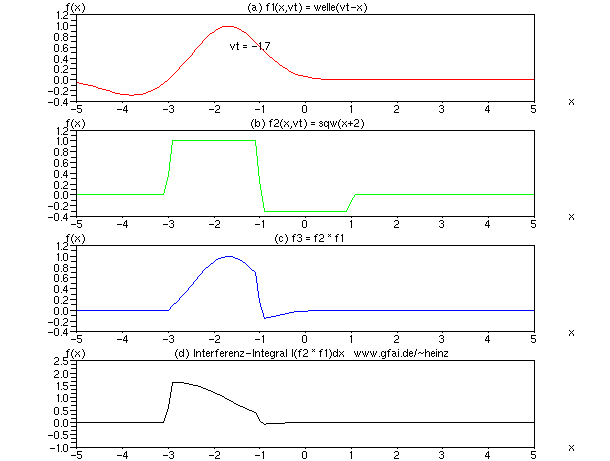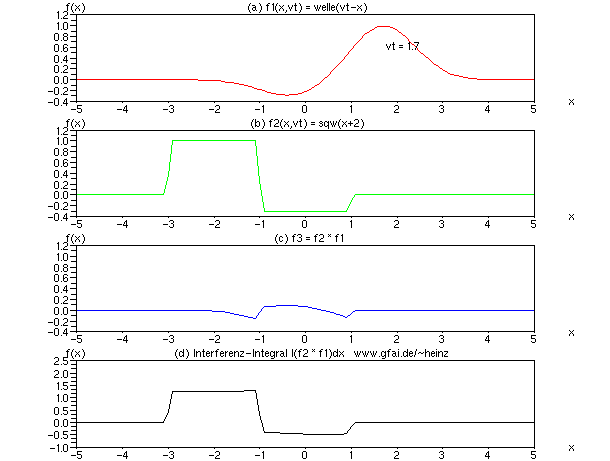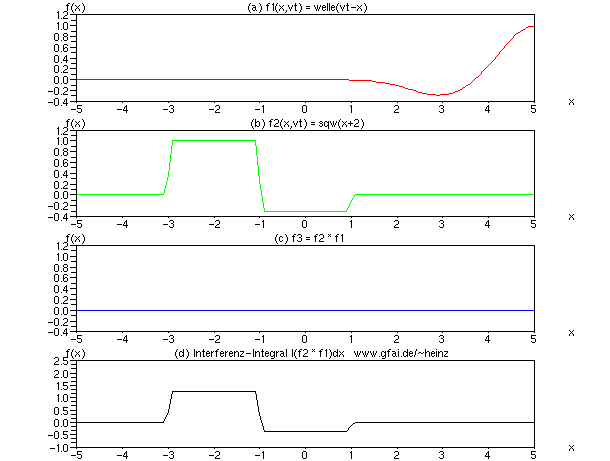
Bild 8: Wir halten Welle (b) an, indem der Parameter vt entfernt wird. Das Interferenzintegral zeigt dann ein skaliertes Abbild der stehenden Welle. Die Form der laufenden Welle ist nahezu bedeutungslos (Scilab-Code unter den Bildern).
Unterschied zum Faltungsintegral: Der Kern von Welleninterferenz erinnert an einen Faltungskern. Allerdings fehlt die verzögerte Mittelwertbildung über mehrere Orte. Im Gegensatz zum Faltungsintegral besitzt das Interferenzintegral nur je einen Ortsbezug pro Schritt. Ausschließlich Amplituden an jeweils einem einzigen Knoten (Sample, Pixel, Voxel, Netzknoten) werden summiert. Daher auch der neue Name. Eine Faltung kann als Interferenznetz dargestellt werden z.B. in Form einer FIR-Schaltung (FIR: Finite Impulse Response). Das Faltungsintegral läßt sich folglich auf Interferenzintegrale reduzieren.
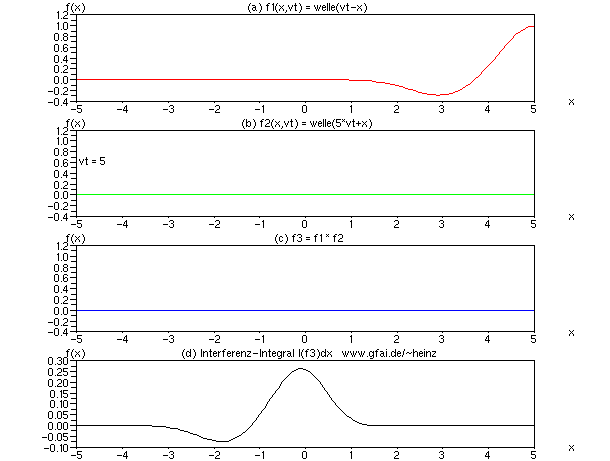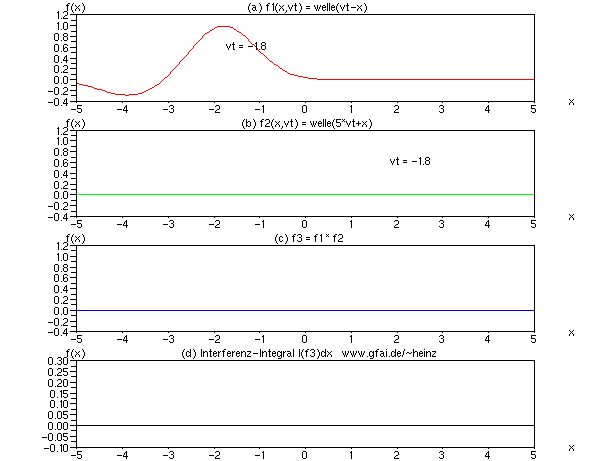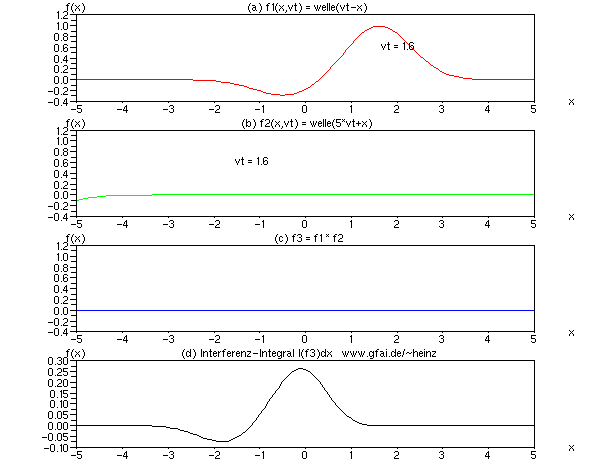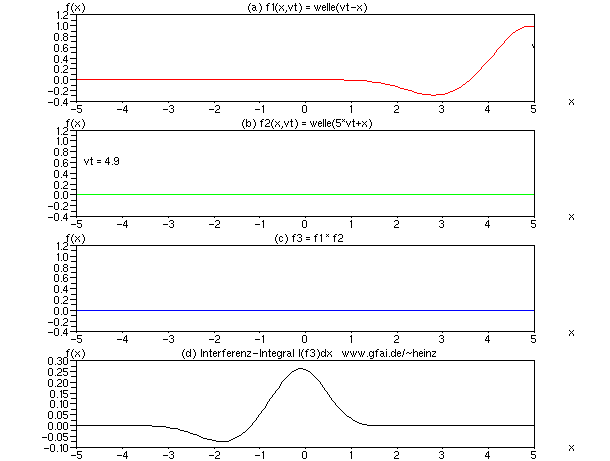
Bild 9: Wir beschleunigen Welle (b), indem der vt-Parameter mit einem Faktor 5 gewichtet wird. Das Interferenzintegral zeigt dann ein gemischtes Abbild beider Wellen, allerdings mit Tendenz zur Darstellung der langsameren Welle. Das resultierende Integral ist schmaler als die langsame Welle (a). Man vergleiche auch die Ausrichtung des Schwanzes beider Wellen.
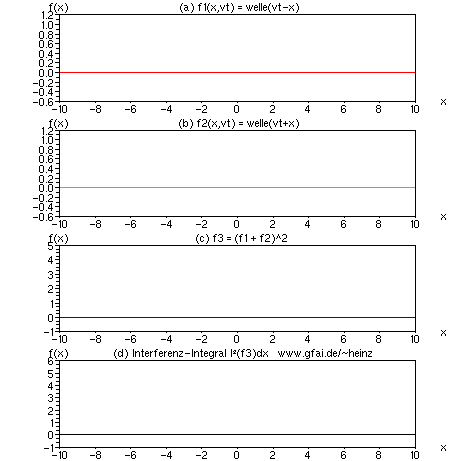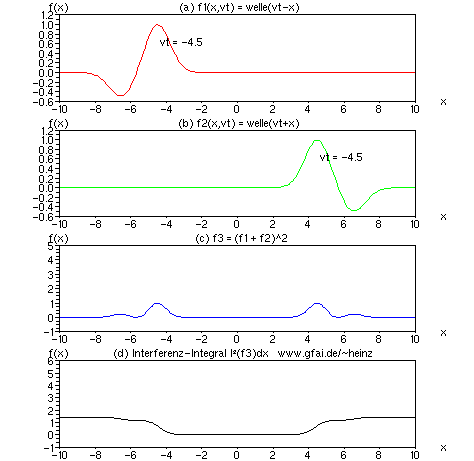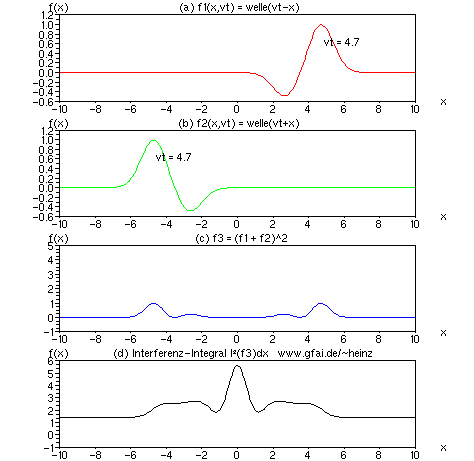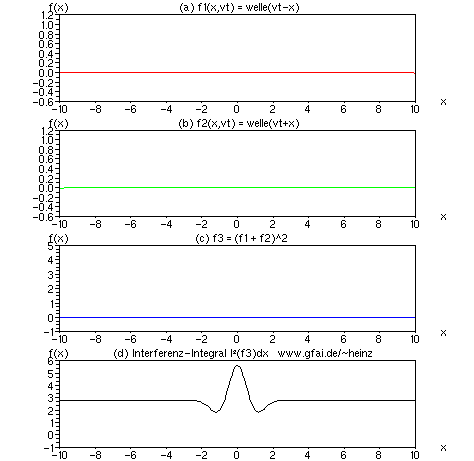
Bild 10: Betrachten wir die Lösung der Wellengleichung nach d'Alembert, so taucht eine Addition zweier Zeitfunktionen (Ortsfunktionen) auf. Die Frage erhebt sich, ob diese Lösung ein von Null verschiedenes Interferenzintegral besitzt. Das Bild zeigt das Ergebnis des Tests für Gauß'sche Wellenformen. Zwar liefern beide Wellenberge bereits einen Gleichanteil im Integral, dennoch hebt sich der Ort der Interferenz ab.
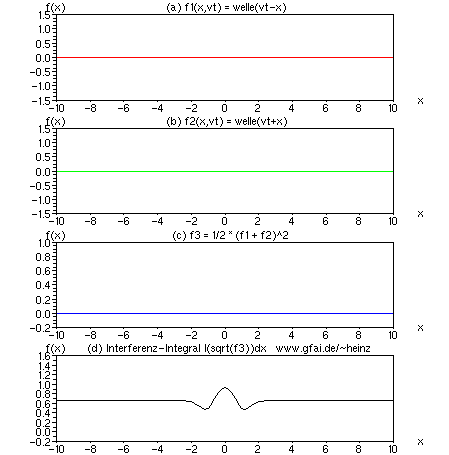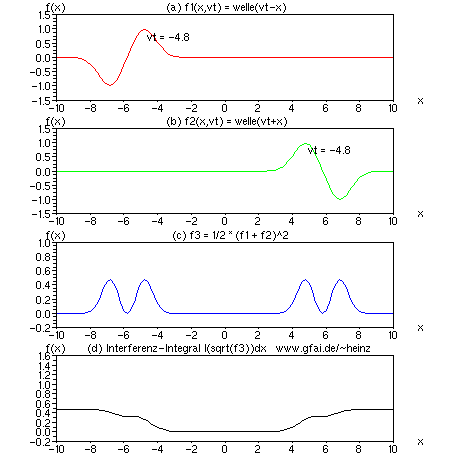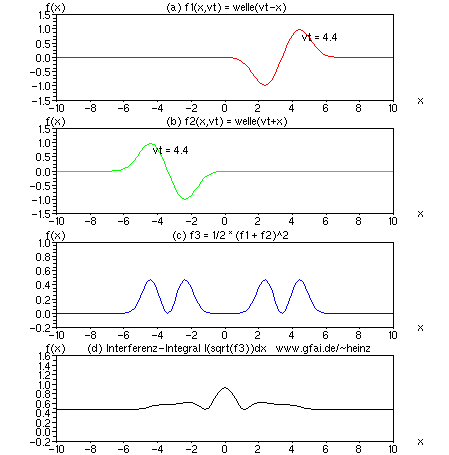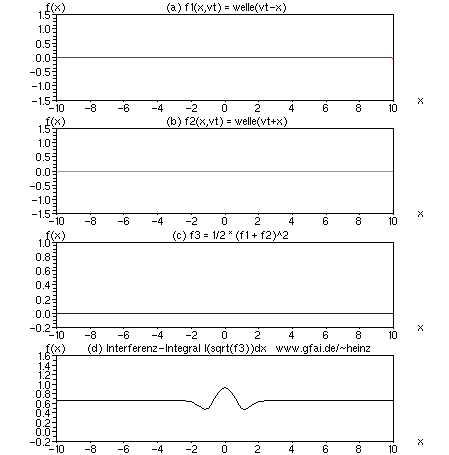
Bild 11: Obwohl im Interferenzintegral (d) weniger Kontrast zu erzielen ist als durch Multiplikation der Zeitfunktionen, ist die Methode aus dem Bereich der akustischen Bildgebung nicht mehr wegzudenken. Verglichen mit der Multiplikation ist sie nicht anfällig gegen mehrkanalige Vorzeichenwechsel.
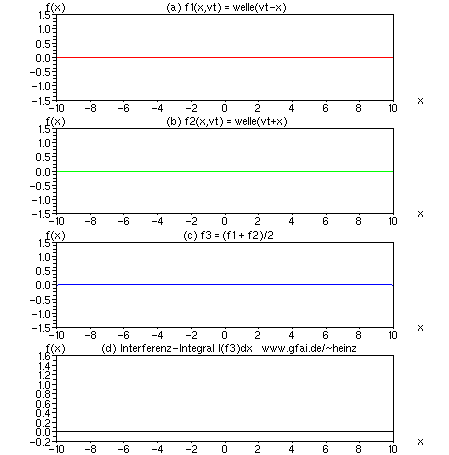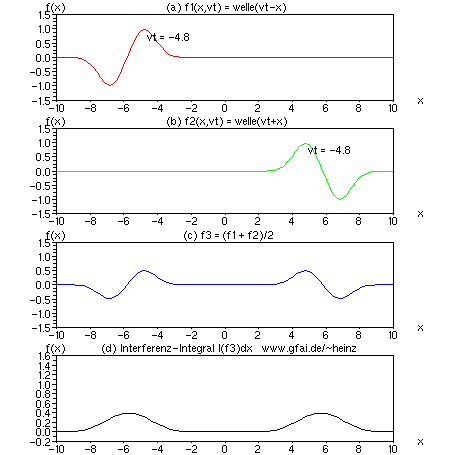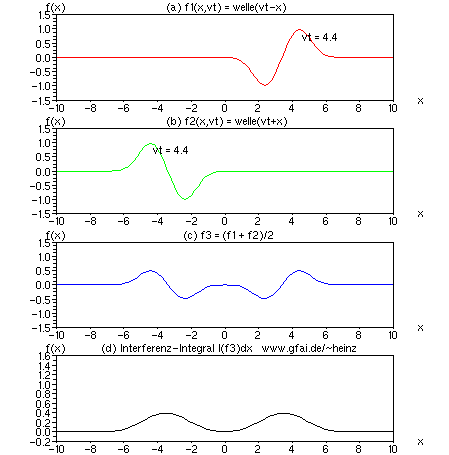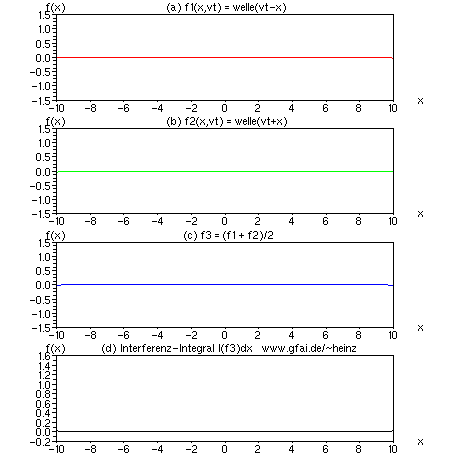
Bild 12: Bei linearer Superposition verschwindet das Interferenzintegral ("Bild") hier vollständig! Man erkennt, daß der positive Wellenabschnitt von (a) oder (b) ein Integral in (d) erzeugt, während der gleichgroße negative Abschnitt das Integral wieder löscht. Im Ergebnis entsteht im Integral eine Welle, aber kein Bild. Diese Simulation zeigt, daß Nichtlinearitäten oder Unsymmetrien (Multiplikation, Quadrat, Effektivwert etc.) nötig sind, um Interferenzintegrale bilden zu können.
Allerdings gibt es Ausnahmefälle:
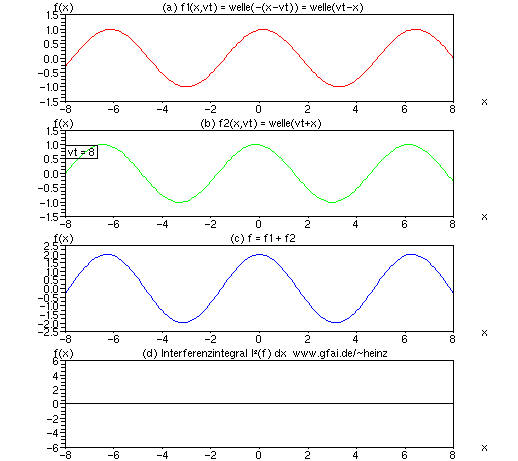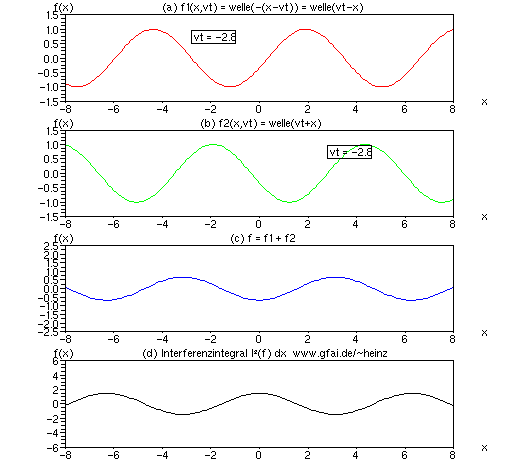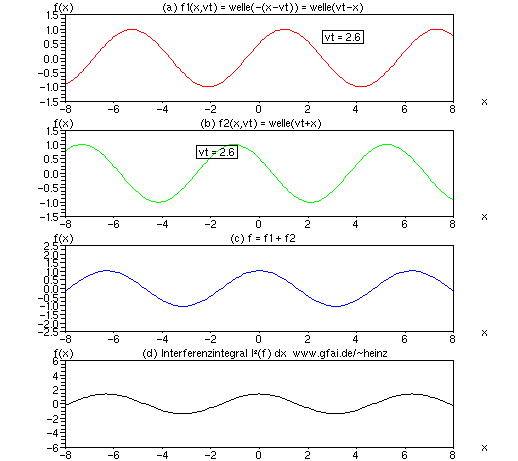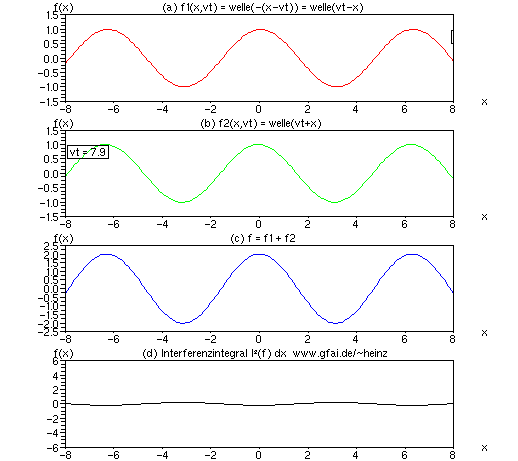
Bild 13: Während die Interferenz einzelner Impulse einen einzigen Ort 'belichtet', bilden sich bei Interferenz mehrerer, von Null verschiedener Wellenzüge an allen Interferenzorten der Wellenzüge von Null verschiedene Interferenzintegrale aus (Fremdinterferenz). Interferenz zweier, sinoidaler Wellenzüge ergibt ständig vorhandene Interferenzen. Bei Addition ist der negative Integralanteil jeweils dem positiven gleichgroß, entsprechend heben sich beide Anteile im Integral auf. Folglich hat man bei Addition immer darauf zu achten, daß eine Nichtlinearität (Quadrat, Potenz) die Interferenzorte anhebt. Außerdem sind u.U. negative Integralanteile ins positive zu klappen (zum Beispiel mit dem Quadrat oder dem Betrag). Das Interferenzintegral der Addition verschwindet latent, es konvergiert offenbar 'schwach' gegen Null (noch ohne Beweis).
Würde man Zeitfunktionen nach ihrer Tauglichkeit für Selbstinterferenz bewerten, so sind die Extrema durch Einzelpuls (Radar, Sonar...) und Sinus (maximales Aliasing) bestimmt.
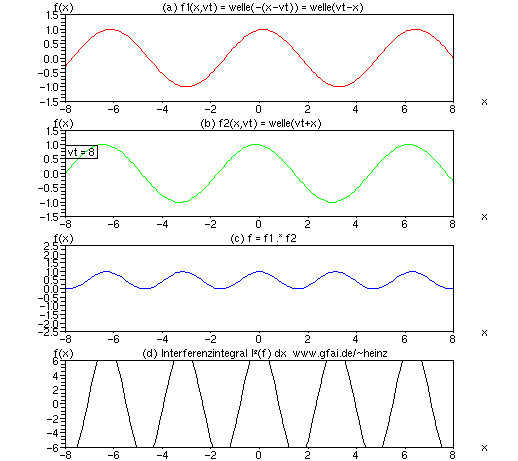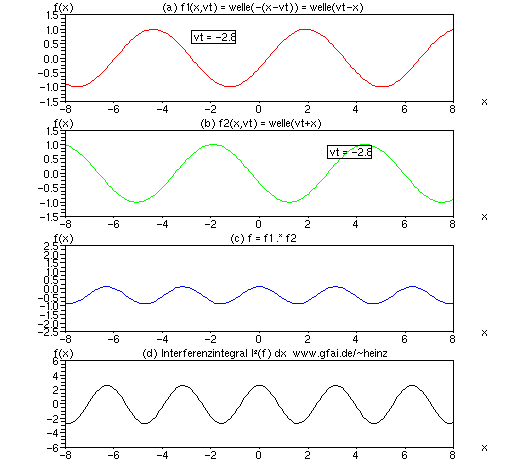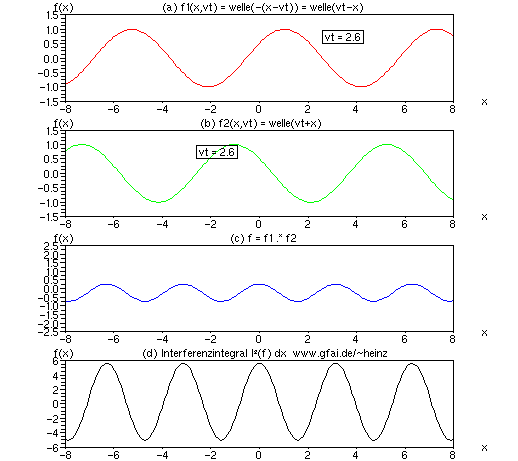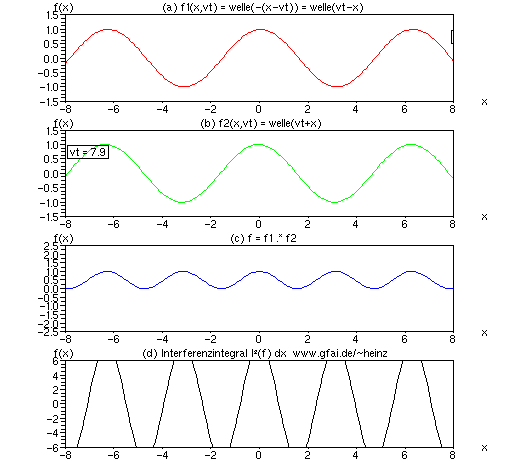
Bild 14: Im Falle multiplikativer Verknüpfung sind beide Forderungen bei zwei Zeitfunktionen automatisch gegeben. Zwei negative Vorzeichen ergeben ein positives Integral; Orte maximaler Interferenz heben sich ab. Entsprechend wächst das Interferenzintegral der multiplikativen Verknüpfung unbegrenzt. Bei Interferenz zweier positiver oder zweier negativer Wellenberge entsteht jeweils ein positiver Beitrag zum Integral, an Orten der Interferenz eines positiven und eines negativen Wertes entstehen negative Integrale. Entsprechend ergibt das Interferenzintegral der Multiplikation einen Sinus doppelter Frequenz und unbeschränkt wachsender Amplitude.
Ein vollkommen anderes Bild ergibt sich bei multiplikativer Verknüpfung von mehr als zwei Zeitfunktionen. Hier entsteht ein permanenter Vorzeichenwechsel, der zu zerissen wirkenden Interferenzintegralen führt. So war die Multiplikation bei der Entwicklung erster, akustischer Bilder und der akustischen Kamera nicht nutzbar. Das Interferenzintegral der Multiplikation divergiert, es konvergiert offenbar gegen +/- &infin (noch ohne Beweis).
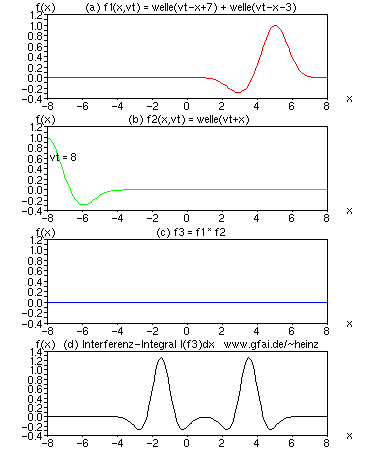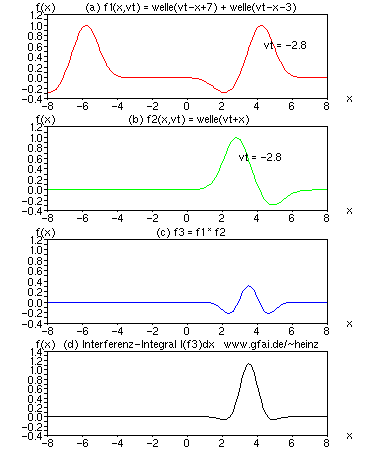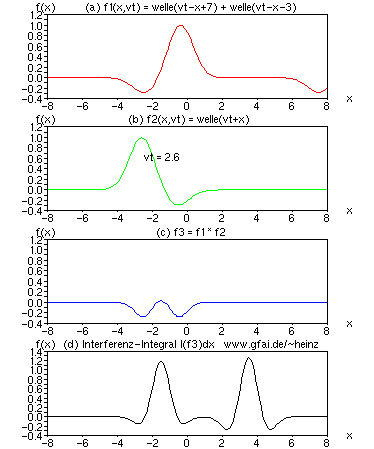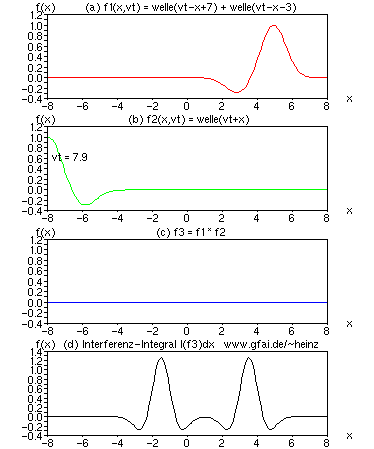
Bild 15: Welle und Folgewelle (Echo, Ton...) in (a) interferieren mit einer anderen Welle (b) und erzeugen unabhängige Prägungen unterschiedlicher Lokalität im Interferenzintegral. Wäre die Folgewelle ein Echo, so würden wir in der Optik von Interferenzfiguren, in der Akustik von Aliasing sprechen.
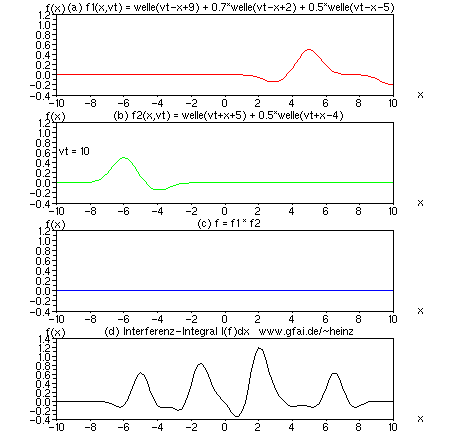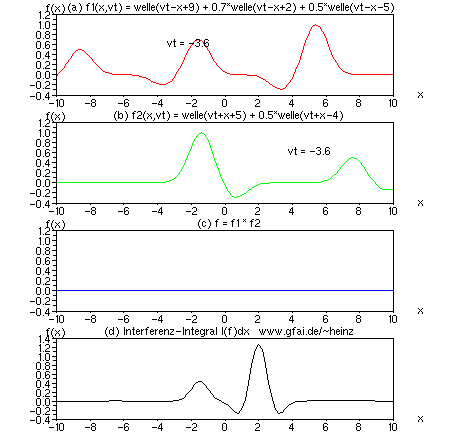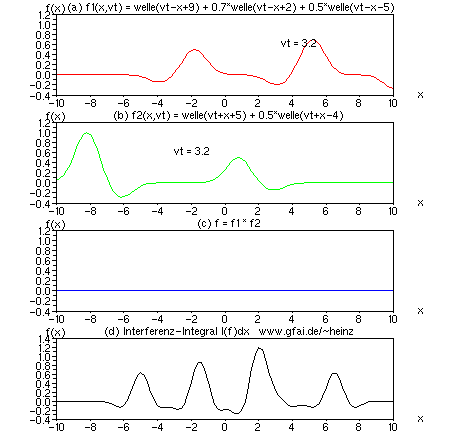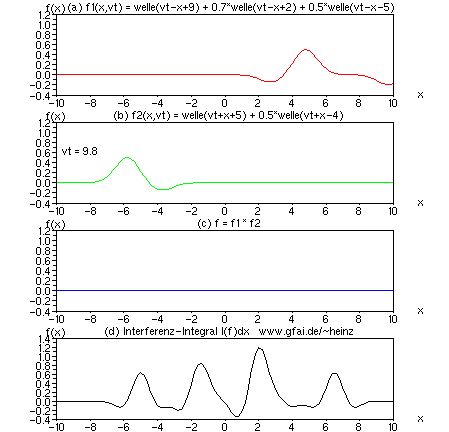
Bild 16: Treffen Wellen mit verschiedener Verzögerung und mit verschiedenen Amplituden aufeinander, entsteht ein Interferenzintegral mit verschiedenen Extrema. Man stelle sich (d) als Schnitt durch ein Photo (Bildzeile) oder durch einen zwei- oder mehrdimensionalen Raum vor, um Interferenzkarten im Nervensystem zu verstehen. Die Verzögerung der Wellen zueinander codiert den Treffort.
Prüft man die Realisierungschance z.B. der verwendeten Zeitfunktion f1(x,vt) als Fouriertransformierte, wird deutlich, daß die Fouriertransformation keinen effizienten Zugang zu Interferenznetzen schaffen kann. Im Gegenteil: Interferenznetze (IN) sind umso effizienter, je weiter die Zeitfunktionen von Sinus und Cosinus entfernt sind. Würde man Zeitfunktionen nach Eignungsgrad für IN sortieren, so wären die ungeeignetsten Sinus und Cosinus, und die bestgeeignetsten Gauß-, Rechteck- oder Dirac-Wellen. Die Evolution erfand wohl nur genau deshalb den Nervenpuls?
Zu den Scilab-Quellen der GIF-Animationen
Unter den GIF-Animationen befinden sich die Scilab-Quellen. Die Scilab-Files erzeugen jeweils eine Bildserie im GIF-Format. Diese kann mit herkömmlichen GIF-Animationsprogrammen, z.B. mit dem
ImageConverter von Polygonsoft (freeware WindowsXP 2006) zu einem GIF-Movie zusammengebunden werden. Hinweis 2024: Quelle ist nicht mehr vorhanden.
Der Aufbau der Scilab-Programme ist ähnlich. Für jeden x-Bereich wird eine Schleife über alle vt durchlaufen. Jedes Ausgabe-Bild wird als separater File im Unterverzeichnis ...\test abgelegt. Damit die Bilder sortiert vorliegen, beginnen sie mit dem Index 1000 im Filenamen. Für längere Movies Indexzähler i erhöhen.
Achtung: Auch Scilab unterliegt beständigem Wandel. Sollte eine höhere Release von Scilab nicht funktionieren, bitte die Version 3.1.1 installieren.
Bitte die Quellangabe nicht vergessen.
Scilab-Source des Wellen-Bildes im Vorwort und Wellen-Bild
Powerpoint-Bilder/Animationen für Interferenznetze/Wellen
Die Zusammenstellung enthält Animationen, die in jeder Form genutzt werden können, vorausgesetzt, die Quelle ist erkennbar gekennzeichnet (http://www.gheinz.de). Für Lehrzwecke können auch die
Powerpoint-Animationen genutzt werden.
top
Created Dec.25, 2006; permanent edited
stylesheet included Oct.14, 2023
Mail to info@gheinz.de
Visited since Dec.6, 2021: