up
english
"The problem of understanding behavior
is the problem of understanding the total action
of the nervous system, and vice versa"
Donald Olding Hebb (1949)
Eine zweite Informatik
Eigenschaften von Interferenznetzen im Überblick
Gerd Heinz
Diese Seite gibt einen Überblick * zu Möglichkeiten, Information mit langsam fließenden Pulsen (Interferenzintegrale und Interferenznetze) zu verarbeiten. Diese unterscheiden sich fundamental von bekannten, digitalen Schaltungstechniken, weshalb wir sie als "Zweite Informatik" bezeichnen wollen.
Hinweis
Die hier als Interferenznetzwerke dargestellten Schaltungen sind keine elektrischen Netzwerke, sondern nervliche Netzwerke mit extrem geringen Leitgeschwindigkeiten. Alle Leitbahnen sind Laufzeitleitungen. Die elektrische Knotenabstraktion einer Leitung gilt hier nicht. Die Überwindung jeglicher Distanz braucht viel Zeit! Und Verzögerungszeiten (Delays) definieren die Funktion des Netzwerks.
Welche Besonderheiten des Nervensystems führten zur Geburt der Interferenznetzwerke?
Überall im Nervensystem finden wir spiegelverkehrte Karten. So finden sich Körperprojektionen im Homunculus spiegelverkehrt wieder, siehe
Kap.8 auf der Seite der Biomodelle.
Solche spiegelverkehrten Abbildungen sind von künstlich-neuronalen Netzen (ANN) nicht bekannt.
Gewichte in ANN werden vom Algorithmus des PC gesteuert über eine quasi unendlich schnelle Fernwirkung.
Auch schreitet die Zeit in diskreten Schritten (Clocks) voran.
Beide Annahmen aber gelten nicht für Nervennetze. Deren Informationsübertragung ist sehr langsam.
Weil auch Taktleitungen viel zu langsam wären, besitzen Nervennetze keinen synchronisierenden Takt.
 Wie ist es möglich, daß eine zwei Millimeter große Fruchtfliege Drosophilidae
(Wikipedia), deren Cortex vielleicht einen zehntel Millimeter groß ist, sich im Raum orientieren kann, ihre Flügel kontrolliert, Nahrung findet und sich vermehren kann? Können wir mit unserer Mikroelektronik und Informatik jemals in diesen Bereich vorstoßen? Oder hat die Natur viel effizientere Möglichkeiten, als wir?
Wie ist es möglich, daß eine zwei Millimeter große Fruchtfliege Drosophilidae
(Wikipedia), deren Cortex vielleicht einen zehntel Millimeter groß ist, sich im Raum orientieren kann, ihre Flügel kontrolliert, Nahrung findet und sich vermehren kann? Können wir mit unserer Mikroelektronik und Informatik jemals in diesen Bereich vorstoßen? Oder hat die Natur viel effizientere Möglichkeiten, als wir?
Wenn wir über leitungsgebundene Informationsverarbeitung nachdenken, dazu zählt auch die nervliche, dann haben wir zunächst zwischen analoger und binärer Verarbeitung zu unterscheiden.
Bei analoger Verarbeitung werden gleitende Werte übertragen. Das können gleitende Spannungswerte sein, wie sie von einem Voltmeter oder Oszilloskop gemessen werden, oder Potentiale, die im EEG oder EKG auftreten.
Bei binärer oder digitaler Verarbeitung hingegen werden nur die Werte Null oder Eins, entsprechend LOW oder HIGH übertragen. Diese Art der Übertragung bietet den Vorteil maximaler Störsicherheit, weshalb sie im Bereich der Technik sehr dominant vorkommt.
Wir unterscheiden zwei Grundformen binärer Verarbeitung:
-
Eine Übertragung, die an eine Uhrzeit (Clock) gebunden ist. Das können Takte sein, oder Baudraten oder Frequenzen, die dem Empfänger die Gültigkeit eines Signals anzeigen.
-
Nerven hingegen haben eine sehr geringe Leitgeschwindigkeit, hier sind Uhren, Baudraten oder Takte unbekannt. Stattdessen finden wir hier überall pulsförmige Signale.
Die Grundfrage zum Verständnis des Nervensystems ist also die Frage nach der Art einer taktfreien Verarbeitung pulsförmiger Signale, die sehr langsam durch die Nerven fließen.
Wie funktionieren sie? Was wissen wir über diese bislang vollkommen unbekannte Gebiet dieser zweiten Informatik? Wir betreten das Gebiet der Interferenznetzwerke (IN).
Wird ein Nerv gereizt, dann antwortet er im allgemeinen mit einem kurzen Impuls. Wird er stärker gereizt, so pulst er schneller, es kommt zu einer Frequenzzunahme. Die Pulsamplitude bleibt dabei stets konstant. Erregung wird in Pulsfrequenz codiert.
Diese Grundform der Signalgebung im Nervensystem finden wir bei allen bekannten Spezies. Für seinen fundamentalen Beitrag zur Aufklärung der Funktion von Nervenimpulsen erhielt Adrian 1932 den Nobelpreis.
Für detaillierte Untersuchungen nervlicher Pulsparameter folgten Hodgkin, Huxley und Eccles mit dem Nobelpreis für Medizin 1963, während Erlanger und Gasser systematisch Leitgeschwindigkeiten verschiedener Nerven untersuchten. John Eccles bemerkte über den Zusammenhang zwischen Faserdurchmesser des Nerven und der Leitgeschwindigkeit:
"Die Leitungsgeschwindigkeit (in m/s) ist annähernd proportional zum Faserdurchmesser (in µm), wobei die Relation für Säugetiernerven etwa 6:1 beträgt; d.h. eine große Nervenfaser von 20µm Durchmesser ... würde Impulse mit etwa 120 Metern pro Sekunde leiten."
(Zitat John Eccles (1973/2000): Das Gehirn des Menschen, Kap.1, S.50)
Der Autor bemerkte 1992, daß eine kurze Pulsdauer t zusammen mit einer langsamen Leitgeschwindigkeit v geometrisch so extrem kurze Pulslängen s erzeugt, daß diese nicht zu unserer digitalen Welt passen. Details siehe folgendes
Kapitel oder
[IWK94].
Im Nervensystem existiert keinerlei sofortige Fernwirkung. Alle Information bewegt sich ionisch und im Vergleich zum Computer extrem langsam. Information breitet sich als Puls nur gleichsam kugelförmig wie eine Welle aus.
Dabei sind Leitgeschwindigkeiten im Nervensystem alles andere als homogen - aus der kugelförmigen Ausbreitung wird eine Wellenausbreitung, die am ehesten die Form einer chaotischen 'Explosionswolke' annimmt.
Die Phantasie des Forschers wird zusätzlich dadurch gefordert, daß sich die Wellenteilchen der Explosionswolke nicht zwangsläufig vom Zentrum weg ausbreiten müssen - die Pulse fließen kreuz und quer auf vielfach gekrümmten Nervenbahnen.
Soll Information verarbeitet werden, dann brauchen wir Eingangssignale, die zur exakt gleichen Zeit auf den Ort der Verarbeitung einwirken.
Sind die pulsförmigen Eingangssignale geometrisch wenige Zehntel Millimeter lang, kann Informationsverarbeitung nur an ganz definierten Orten stattfinden, nämlich dort, wo sich Pulse begegnen. Da sich dieser Ort aber ändert, sobald nur ein einziger Puls früher oder später eintrifft, ist Verarbeitung an einem Ort nur möglich, wenn Pulsmuster kohärent (d.h. mit unveränderter Zeitdifferenz) auftreten. Da Sensor- und Aktorfasern letztlich an diskreten Orten in ein Nervennetz münden, entsteht die Frage, wie die Informatik des Netzes letztlich beschaffen sein muß, um zu erreichen, daß viele, bei der zu lösenden Aufgabe zu verarbeitende Pulse zeitgleich an genau diesem Ort zum Beispiel eines Aktoranschlusses für einen spezifischen Muskel eintreffen. Was also bedeutet die Forderung nach lokaler Kohärenz für die Informatik der Netze?
Die höchste aufgezeichnete Zahl von Synapsen eines Neurons beläuft sich auf 80.000 ([Eccles] S.134).
Ein Pyramidalneuron des Cortex möge beispielsweise 10.000 Synapsen besitzen. Der Schwellwert zur Erregung möge dazu zwischen 0% und 90% variieren können (fuzzy OR- bis AND- Verhalten). Dann heißt das, daß für eine AND-artige Erregung des Neurons 9000 Synapsen kohärent erregt werden müssen: bis zu 9000 winzig schmale Pulsspitzen müssen genau zum richtigen Zeitpunkt die richtige Synapse des Neurons streifen, damit es erregt werden kann. Hier entsteht sofort die Frage: Wie ist eine so extreme Präzision in einem Netzwerk mit höchsten, absoluten Parameterschwankungen erreichbar? Wie kann solche Präzision in einem Netzwerk erreicht werden, bei dem vierzig bis hundert Milliarden Neuronen miteinander flexibel interagieren?
Um es anders zu sagen: Sind im Nervensystem fließende Pulse geometrisch kurz im Vergleich zum adressierten Raster, werden nur dort Informationen verarbeitet, wo Pulse kohärent positiv interferieren. Zeitliche Muster werden damit zu räumlichen Codes. Ein Code wird nun nicht mehr von einem Neuron X, Y oder Z verarbeitet, sondern jedes zeitliche Muster adressiert andere Neuronen. Verarbeitet wird eine Information dort, wo Zwillinge eines Pulses gleichzeitig wieder zusammentreffen, wo diese (positiv) miteinander interferieren. Damit entsteht ein erweiterter Wellenbegriff. Und es entsteht ein Wellenmodell des weit verzweigten Neurons. Die daraus entstehende Informatik hat nicht das geringste mit digitaler Schaltungstechnik oder Boolscher Algebra zu tun.
Aus der Optik kommend (Prismen), waren Wellentheorien bislang im Spektralbereich (Fourierbereich) angesiedelt. Da aber Pulsmuster nicht zu spektralen Transformationen (Fourier) passen, war zunächst eine Wellentheorie im Zeitbereich zu entwickeln, die diskrete und inhomogene Räume neuronaler Art einschließt. 1993 wurden die wichtigsten Merkmale im Manuskript "Neuronale Interferenzen"
[NI93]
skizziert. Fast alle später diskutierten Ideen gehen auf dieses Manuskript zurück. Oft sind sie dort einfach zu kurz, zu schwach oder zu schwer verständlich angerissen.
Zurück zur Kohärenz interferierender Pulse. Kohärente Pulsinterferenzen sind denkbar in Form spiegelverkehrter Abbildungen selbstinterferentieller Art und spektraler Karten fremdinterferentieller Art. Dort, wo eine Pulswelle mit sich selbst interferiert, erzeugt sie eine spiegelverkehrte Abbildung, eine Projektion. Dort, wo sie mit ihren (kohärenten) Vorgängern oder Nachfolgern interferiert, entsteht eine spektrale Kartierung. Sehen und Hören verschmelzen miteinander. Es entsteht eine neue, bislang unbekannte Art von Kommunikation und Informationsverarbeitung. Ende 1996 entstand für verzögernde, pulsende Netzwerke der Begriff der 'Wave Interference Networks'.
Der Versuch des Autors, nervliche Pulse mittels Datenrecorder und Software aufzunehmen und deren nervliche Projektionen zu berechnen, war nicht zuletzt aus kommerziellen Gründen nur bedingt erfolgreich, siehe [BIONET96].
Dagegen brachten an den Datenrecorder angeschlossene Mikrofone die ersten, akustischen Bilder hervor. Akustische Experimente mit dem Interferenz-Simulator Bio-Interface/PSI-Tools (Parallele und Serielle Interferenz - Werkzeuge) zeigten weltweit die ersten (stehenden, passiven) Schallbilder und Schallfilme, die akustische Photo- und Kinematographie und der Begriff "Akustische Kamera" wurden als erste Applikation einfachster Interferenznetzwerke geboren.
Auch in der Akustik haben wir es mit sehr verschiedenen Wellenlängen zu tun. Mit
λ = v/f reichen sie von 3,4 Meter bei f = 100 Hertz bis zu 17 mm bei 20 kHz (bei v = 340 m/s).
Betrachtet man die Theorie der Interferenznetzwerke, so erweitert sie physikalische Wellentheorie in zwei Richtungen: Zum einen wird der Wellenbegriff auf extrem inhomogene und diskrete Laufzeiträume, nämlich auf Nervennetze erweitert und zum anderen zwingen Pulsmuster dazu, den Spektralbereich zu verlassen und eine Wellentheorie im Zeitbereich zu beginnen.
Offenbar nur deshalb, weil die Wellentheorie im Zeitbereich zunächst überschaubarer und handhabbarer war, als konkurrierende Wellentheorien im Frequenzbereich (Beamforming), trat die
Akustische Kamera
als erste die weltweite Markteinführung an. Simulationen mit Bio-Interface/PSI-Tools bestätigten schon 1994 einen algorithmischen Kern (Interferenzrekonstruktion), der das Problem der Überbestimmtheit vollständig löst: Im Gegensatz zur achsfernen Unschärfe optischer Linsensysteme arbeitet die akustische Kamera bei beliebiger Kanalzahl mit beliebig weitem, auch achsfern scharfem Bildfeld, siehe [DAGA07].
Mit ersten Ideen zum Interferenzansatz und zu Wellen auf Leitbahnen war im Jahre 1992 noch nicht sicher, ob die Theorie der Interferenznetzwerke tatsächlich auf Nervennetze anwendbar wäre. Entsprechend vorsichtig waren meine Formulierungen in bislang allen Veröffentlichungen.
Erst im Laufe vieler Publikationen und Diskussionen wurde mehr und mehr transparent, daß der Interferenzansatz nicht von hypothetischer, sondern von systematischer Natur ist. Zum einen sprechen die vielen, zufälligen Übereinstimmungen diskutierter Netzwerkstrukturen mit bekannten Forschungsergebnissen oder Verhaltensmustern dafür. Zum andern läßt sich die theoretische Abhandlung so gliedern, daß sie in ihren Teilen systematisch und nachvollziehbar wird.
Wollen wir den Interferenzansatz objektiv bewerten, stehen Eccles Erkenntnisse zur synaptischen Übertragung im Mittelpunkt. John Eccles verfocht anfänglich eine (verzögerungsfreie) elektrische Übertragung des Pulses an der Synapse, wies dann aber bei höheren Organismen eine langsame, vorwiegend chemische Übertragung nach. Eric Kandel erforschte Details. Die chemische Übertragung wiederum kann zusätzlich integrierende Wirkung besitzen: zum Beispiel an einer neuromuskulären Endplatte (vgl. Eccles: Gehirn des Menschen, Kap.II und III, S.107). Die Ausbildung des excitatorischen oder inhibitorischen, postsynaptischen Potentials (EPSP, IPSP) zeigt offenbar überall eine kleine, integrierende Wirkung. Ein EPSP/IPSP-Puls scheint eine Zeitkonstante zu besitzen, die etwa zehnfach länger als der sie auslösende Puls ist. Genauere Untersuchungen zu Pulsrelationen an der Synapse sind allerdings bislang nicht bekannt.
Bei allen Simulationen neuronaler Projektionen wird deutlich, daß ein Zusammenrutschen einer Projektion mit deren fremdinterferentiellen Geisterbildern allein über die Refraktärzeit (Pulspause) bestimmt wird, siehe
Schmerzsimulation. Die Pulspause muß mehr als zehnfach länger als der Puls sein, sonst erzeugen wir Potentiale. Deshalb stört ein langes EPSP/IPSP eher kaum.
Der Begriff des Pulses ist relativ zu sehen. So ist eine Untersuchung mit radioaktiv markiertem Leucin [Ochs72] bekannt, bei der sich eine Pulswelle mit einer Ausbreitungsgeschwindigkeit von 4,75 µm/s oder 410 mm pro Tag bewegt, siehe auch
[NI93]
, Kap.11, S.220. Nehmen wir an, ein Puls dauert eine Stunde an, dann hätte der Puls eine geometrische Pulsbreite von rund 410/24 mm = 17 mm. Es entsteht unweigerlich die Frage, ob man derart langsame Signale überhaupt beobachten kann. Ableitungen jeglicher Art sind meist nur wenige Sekunden oder Minuten stabil. Eine so langsame Welle wird von einem Beobachter nicht als Welle, sondern als statisches Potential wahrgenommen.
Problematisch bleibt bis heute, daß noch immer kaum belastbare Daten zu geometrischen Pulsbreiten in verschiedensten Nervenfaserteilen bekannt wurden. Auch Fragen der Gewichtung erscheinen längst nicht so klar: Wichtet die einzelne Synapse, oder werden dendritische Äste am Zugang zum Soma gewichtet?
Die Arbeiten zu Interferenznetzen zeigen, daß diese Fragen bedeutsam geworden sind.
Eine Betrachtung der Wellenauslöschung auf dem Ischias-Nerv des Frosches zeigte schon vor hundert Jahren, daß ein Nervenabschnitt, der an mehreren Stellen aufeinander folgend bombardiert wird, mitnichten als Schwellwertgatter modellierbar ist. Gegeneinander laufende Pulse löschen sich aus, wenn sie in die Refraktärzone des anderen laufen. Wenn Schwellwertlogik damit kein Ansatz zur Modellierung von Nervennetzen ist, haben wir uns zu fragen, wie es weitergehen kann.
Verschiedentlich kam von interessierten Wissenschaftlern die Aufforderung, die Theorie der Interferenznetzwerke (IN) mathematisch klarer faßbar darzustellen. Versuche folgten. Meist hatten sie dasselbe, frustrierende Ergebnis: Das allgemeine Prinzip wurde einer im Einzelfall zutreffenden Formel oder Anschauung geopfert. Die Tendenz ist zunehmend bei jüngeren Konferenzbeiträgen anzutreffen.
Dies ist insofern bedeutsam, als daß selbst Grundansätze des Neurocomputing, also sehr übliche Beschreibungsmethoden wie z.B. Schwellwertlogiken, durch Betrachtungen interferenzieller Art nur noch in Ausnahmefällen haltbar sind. Die Kommentierung wird sich folglich so wenig wie möglich auf mathematische Details konzentrieren.
Wir werden versuchen, die harten, informatischen Konsequenzen, die unzweifelhaft aus Puls-Interferenzen auf verzögernden Netzwerken resultieren, zu beleuchten. Wir setzen dabei meist voraus, daß sich die geometrischen Wellenlängen etwa im Bereich des betrachteten, neuronalen Rasters bewegen.
Wie wir sehen, haben Interferenznetze überhaupt nichts mit Computer Science zu tun. Wir haben eine zweite Informatik zu entwickeln!
Für weitere Recherchen nutze der geneigte Leser bitte das
Publikationsverzeichnis oder die historischen Seiten. Interferenzmodelle zum Nervensystem sind unter Biomodelle und als
Animationen zu finden. Zu mathematischen Grundlagen lese man das Buch "Neuronale Interferenzen" (german) oder "Virtual Experiments" (english). Leitgeschwindigkeiten werden in [IWK94] diskutiert
(english and german).
Der Autor bemerkte 1992, daß eine kurze Pulsdauer T zusammen mit einer langsamen Leitgeschwindigkeit v geometrisch so extrem kurze Pulslängen s erzeugt, daß diese nicht zu unserer digitalen Welt passen. Details siehe [IWK94].
Die geometrische Pulslänge s ergibt sich dabei aus dem Produkt von Leitgeschwindigkeit v und Pulsdauer T,
s = v·T
Für Eccles Beispiel variieren die geometrischen Pulslängen mit der Dauer von einer zehntel Millisekunde (T = 0,1 ms) gemäß s = vt von s = 12 mm (für v = 120 m/s) bis zu s = 0,12 mm (für v = 1,2 m/s). Faser-Typ C nach Erlanger-Gasser erreicht sogar nur 0,5 m/s, die geometrische Pulsbreite geht hier bis auf s = 50 µm zurück.
Wir stellen fest, daß es sich um Pulslängen handelt, die einem Sonar oder Radar zur Ehre gereichen würden! Wie aber verknüpft man so extrem kurze Pulse? Wie soll damit eine Informationsverarbeitung geschehen?
Eine sinnvolle Verknüpfung von Zeitfunktionen mit so kurzen Impulslängen ist nahezu unmöglich. Um sie verknüpfen zu können, müssen die Impulse auf die Mikrosekunde genau gleichzeitig an einer Nervenzelle ankommen.
An dieser Stelle hört man immer das Argument von der Integrationszeit der Neuronen. Daß das aber unsinnig ist, zeigen nicht zuletzt die Milliarden Pulse, die ständig in unserem Kopf umherschwirren und die Neuronen aus allen Richtungen befeuern. Indes wird Integration dringend gebraucht - aber erst nach der Verknüpfung der Inputs, erst nachdem das Neuron begriffen hat: "Ach - ich bin gemeint!"
Wenn ein Neuron ständig aus allen Richtungen befeuert wird - was macht es dann? Es wird träge! Es reagiert nur noch in der Mikrosekunde, in der sehr viele Synapsen gleichzeitig eine Pulsspitze empfangen. Danach braucht es eine Weile, um wieder zu regenerieren. Es erholt sich und senkt langsam seinen Schwellwert. Bis es wieder von vielen Pulsen getroffen wird, die exakt zur selben Zeit ankommen.
Sortiert man praktisch vorkommende Leitgeschwindigkeiten v und zugehörige Pulsdauern T nach deren Produkt vT, der geometrischen Pulsbreite
[IWK94], dann bemerkt der aufmerksame Beobachter eine Korrelation zwischen geometrischer Pulsbreite und funktionalem Raster. So ist die geometrische Pulsbreite bei Muskeln größer, als im Cortex.
Während eine geometrische Pulsbreite von zwölf Millimetern eher zu einer Muskelansteuerung paßt, erreichen wir mit fünfzig Mikrometern das kolumnale Raster des Cortex.
Mehr dazu siehe [NI93] oder [IWK94].
Verschiedene Messungen an Neuronen zeigten, daß die Dauer der pulsförmigen Entladung durchaus von der Länge der vorhergehenden Feuerpause mitbestimmt wird. Unter der Annahme, daß ein ausgeruhtes Neuron etwas länger feuert, variiert also auch die Pulsdauer T ein wenig.
Nehmen wir eine Verdopplung der Pulsdauer an, so verdoppelt sich damit auch die geometrische Pulsbreite. Was könnte das bedeuten?
Es bedeutet nicht mehr und nicht weniger, als das das Neuron versucht, seinen Adreßbereich zu vergrößern!
Längenproportionale Verzögerungszeiten der Nerven erzeugen automatisch und unabänderlich eine dynamische Adressierung, eine Kartierung in den Raum hinein, siehe Abb.2-1. Entstehende Interferenznetze (IN) sind dadurch in Zeit und Raum gleichzeitig angesiedelt, es entstehen Karten in Raum und Zeit, neudeutsch "spatio-temporal maps".

Abb.2-1: Adressierungsprinzip in verzögernden Pulsnetzwerken. Fall #1 steuert Neuron N2 an, während Fall #2 das Neuron N1 aktiviert, vorausgesetzt, der Laufzeitunterschied zwischen a und a' sowie b und b' beträgt τ und die Neuronen besitzen einen Schwellwert vom AND-Typ.
In Abb.2-1 betrachten wir zwei Neuronen N1 und N2, deren Schwellwerte so hoch eingestellt sind, daß sie AND-Verhalten zeigen. Nur wenn beide Eingänge der Neuronen N1 und N2 zeitgleich einen Puls erhalten, kann der Ausgang aktiviert werden.
Endliche Leitgeschwindigkeit erzeugt die Verzögerungszeiten a, a', b, b' auf den Leitbahnen. Die Verzögerungen a und a' sowie b und b' mögen sich je um τ unterscheiden mit
a' - a = τ
b' - b = τ
Nun legen wir an den Stellen A und B zwei um τ verzögerte Pulse an, Abb.2-1 unten. Im Fall 1 möge der Puls an A zuerst erscheinen, im Fall 2 möge der Puls an B vorangehen. Während im Fall 1 nur Neuron N2 erregt wird, wird im Fall 2 nur Neuron N1 erregt.
Die Verzögerungen (Delays) der Leitbahnen sorgen folglich dafür, daß ein sich änderndes, zeitliches Muster einen sich ändernden Ort adressiert. Hätten unsere zwei Neuronen gewichtslernende Eingänge Hebb'scher Prägung, so würde ihnen das nicht viel nutzen. Sie könnten nur lernen, überhaupt nicht zu reagieren.
Um unser Beispiel weiter zu rechnen: N2 möge der Anfang eines efferenten (absteigenden) Motoneurons sein. Um den betreffenden Muskel anzusteuern, muß genau der Ort von N2 erregt werden. In Abb.2-1 ist dies nur möglich mit der Kombination der um τ zeitversetzten Zeitfunktionen an den Punkten A und B nach Fall 1.
Möge τ eine Millisekunde lang sein, dann bestünde zwischen den Pfaden bei einer Leitgeschwindigkeit v von 1,2 m/s eine Längendiffererenz ds von 1,2 Millimetern: ds = v τ = 1,2 m/s · 1 ms = 1,2 mm. Das ist extrem wenig!

Abb.2-2: MacDougalls Reflexbogen. Quelle: Sherington, Charles: The Integrative Action of Nervous System, 1906, Fig.56, p.201, unter Bezug auf Ref. 262: MacDougall, W.: Brain, Part cii, p.153
Sehen wir uns die über hundert Jahre alte Skizze an, Abb.2-2, so könnten wir einen Interferenzkreis in der Konstellation erkennen, die in Abb.2-1 beschrieben ist.
Aber die Idee MacDougalls war es wohl eher, daß eine Erregung des Flexors den Extensor hemmt und umgekehrt.
Wären die zwei Synapsen, die an jedem Neuron andocken, von verschiedenem Typ (erregend oder hemmend), würde die Schaltung statisch funktionieren, sie würde dafür sorgen, daß nur der eine oder der andere Muskel erregt werden kann. Allerdings ist dies in Abb.2-2 nicht zu erkennen.
Neuere Erkenntnisse (Crick & Asanuma, 1986 in PDP, Vol.2, S.338) besagen aber:
"No axon makes Type1 synapses (exciting) at some sites while making Type2 (inhibiting) at others."
Dies würde eine statische Funktion der Schaltung ausschließen, die Schaltung würde dann, nur wie in Abb.2-1 gezeigt, dynamisch arbeiten. Grundlagen und Details zu Wettlaufschaltungen sind hier zu finden, siehe
[Virtual Experiments] und
[NI93].
Liest man hingegen Eccles, so bestünde auch die Möglichkeit einer statischen Interpretation. Sinngemäß schreibt er, daß inhibitorische Synapsen ausschließlich am Zellkern, excitatorische Synapsen nur selten am Zellkern andocken. Wären die zwei Synapsen, die an jedem Neuron andocken, von verschiedenem Typ, würde die Schaltung auch statisch funktionieren, sie würde dafür sorgen, daß nur der eine oder der andere Muskel erregt werden kann.
Erweitern wir dieses Adressierungsmodell um weitere Neuronen (in Abb.2-3), so erkennen wir, daß die Relativität im Vorankommen der Pulse zwischen A und A' den Ort der Interferenz, den Zielort der Information bestimmt. Deshalb wurden solche Netzwerke vom Autor als Interferenznetzwerke (IN) eingeführt.
Gleichzeitig bemerken wir in Abb.2-3, daß zwischen einem generierenden Feld (unten) und einem empfangenden Feld (oben) eine spiegelverkehrte Abbildung von P auf P' entsteht. Die Abbildung entsteht dort, wo auf allen Pfaden zwischen sendendem und empfangendem Neuron gleiche Laufzeit herrscht.

Abb.2-3: Erste Skizze einer einfachsten, neuronalen Abbildung (Pulsprojektion), Titelseite des Buchs
Neuronale Interferenzen, 1993.
Im Empfangsraum M mögen sich Neuronen mit einer multiplikativen Eigenschaft (AND-Typ, Null siegt) befinden.
Ein sendender Raum S interferiere über zwei Axonen A und A' mit einem Empfangsraum M.
Nur dort, wo Pulse von einem Quellneuron gleichzeitig wieder ankommen, entsteht neue Erregung. Erregung vom Neuron am Ort P wird damit an ein Neuron an einen Ort P' weitergegeben - oder einer Bildvorlage P wird ein spiegelbildliches Abbild P' zugeordnet.
Wir kennen genau diese Eigenschaft von der Optik der Linsenabbildungen. Und wir erahnen, daß die Empfangszuordnung über Laufzeiteigenschaften des verbindenden Netzwerkes definiert ist.
Dieser einfachste, neuronale Interferenzkreis (Abb.2-3) wurde wegen seiner optischen Analogie als Titelbild für das Manuskript
Neuronale Interferenzen (1993)
ausgewählt. Die Entdeckung spiegelverkehrter Abbildungen in "neuronalen Netzen" stellte 1993 für Eingeweihte eine Sensation dar, waren doch spiegelverkehrte Karten aus der Anatomie bekannt (Homunculus), nicht aber aus der Netzwerkforschung (neuronale Netze).
Die Informationsverarbeitung liegt folglich in der Überlagerung (Interferenz) lokal am Neuron zeitgleich ankommender Pulse. Und Gleichzeitigkeit des Ankommens bedeutet im Umkehrschluß, daß neben Gewichten die entscheidende Rolle zum Verständnis der Informatik eines Nervennetzes der Verzögerungsstruktur des Netzwerkes zukommt.
Dies unterscheidet sich grundlegend von der digitalen Elektronik, die wir verwenden. Ausnahmen sind GPS, RADAR oder SONAR.
Da sich die zeitliche Struktur des Netzwerks sowohl in den fest verdrahteten Delays, als auch im eingespeisten zeitlichen Code dokumentiert, besitzt jedes Geräusch und jede Frequenz eine eigene, typische Verzögerungsadresse.
Jeder Ort im Nervennetz besitzt damit über sein spezifisches Verzögerungsnetz eine Adresse. Er kann nur über ein dem Netz der Verzögerungen entsprechendes zeitliches Muster adressiert werden.
Die Frage nach der Langsamkeit von Impulsen beantwortet sich dabei über die geometrische Pulslänge als Produkt aus Leitgeschwindigkeit und Pulsdauer. Diese bestimmt letztlich das von einem Puls kartierbare, neuronale Raster, Abb.2-3. So werden wir zur Muskelansteuerung Wellenlängen im Zentimeterbereich brauchen, für intra- kortikale Kommunikation hingegen sind Wellenlängen im Mikrometer- oder Millimeterbereich gefragt. Letztlich liegen bekannte Pulsdauern im Bereich zwischen Mikrosekunden und Tagen, meßbare Leitgeschwindigkeiten zwischen Mikrometern und Metern pro Sekunde.
Das Lernen biologischer Wesen ist unendlich viel komplexer, als es Hebbs Rule oder die tausenden Aufsätze zu ANN suggerieren mögen. Eine bis heute interessante Übersicht über die Erforschung biologischen Lernens von Harrington, Rosenthal bis Penard, Thorpe oder Pawlov (um nur wenige zu nennen) und verschiedenste Lernversuche an unterschiedlich intelligenten Lebewesen und deren komplexe Interpretationen gibt der Gründungsvater des "Zentralinstituts für Kybernetik und Informationsprozesse"
(AdW-ZKI) Friedhart Klix
(siehe Wikipedia) in dessen Buch "Information und Verhalten" (1970 Verlag Hans Huber, Bern, Stuttgart, Wien; Lizenzausgaben VEB DVW Berlin 1973, 1976).
Dieses Buch ist insofern einmalig und interessant, als es (noch) nicht die technische Seite der kommenden Kybernetik, sondern ausschließlich die biologische, experimentell beobachtbare Seite beschreibt und in stochastische Modelle zu gießen versucht. Wer glauben mag, etwas vom Lernen zu verstehen, wird sich schnell eines besseren belehrt fühlen.
Die dutzenden, von Klix erörterten Lernmodelle von Lebewesen sind derart komplex, daß man nur staunen kann. Er beschäftigt sich im Kapitel 6 ("Über Wesen, Eigenschaften und Grundgesetze organismischer Lernprozesse") ausgibig mit dem Thema. Und er bietet eine Lerndefinition an, deren Abstraktion überraschen mag, die aber Lernprozesse höherer Individuen ebenso umfaßt, wie die an bewegungsfähigen Einzellern (Paramaecium) beobachtbaren.
Er schreibt in Kap.6, S.347:
"Mit Lernen bezeichnen wir danach jede umgebungsbezogene Verhaltensänderung, die als Folge einer individuellen (systemeigenen) Informationsverarbeitung eintritt."
Bei der Erforschung von Lernverhalten von Lebewesen zeigt Klix eine Zusammenstellung zur Lerndynamik.
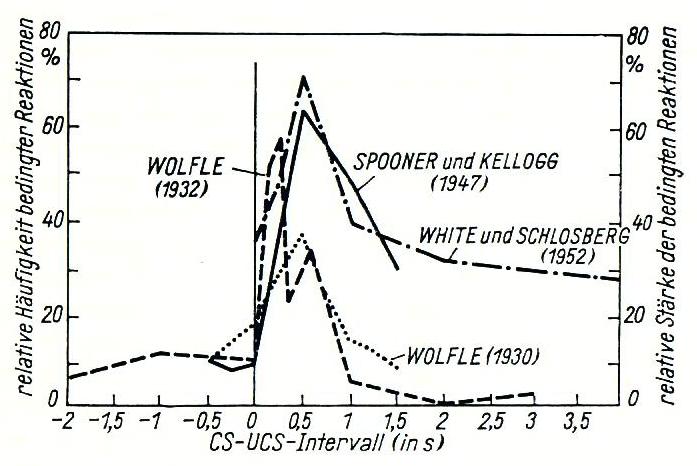
Abb.3-1: Der Einfluß des Zeitintervalls auf die Bildungsgeschwindigkeit bedingter Reaktionen. CS stellt einen bedingten Reiz dar (z.B. Glocke), UCS den Unbedingten (z.B. Presentation von Nahrung; Null-Linie). Man erkennt ein zeitliches Optimum für die Ausbildung einer Reaktion im Bereich Δt = tCS - tUCS = 0,3...0,7 s. (Nach Klix, Abb.6.5, S.368)
In Abb.3-1 können wir uns unter UCS zum Beispiel das Leuten einer Glocke und unter CS die Präsentation von Nahrung vorstellen. Hierbei kann ein Lernvorgang erfolgen, der eine Erregung ausbildet. Wird hingegen ein Teil der Versuchsbox bei CS unter Spannung gesetzt, wird ein hemmungsausbildender Lernvorgang erfolgen, das Tier wird diesen Bereich fluchtartig nach Leuten der Glocke verlassen.
In allen Fällen wird mit größer werdendem Δt der Lernerfolg geringer. Für Werte Δt < 0 bleibt der Lernerfolg nahezu aus.
Es wird deutlich, daß Lernen nie ein einzelner, isolierter Vorgang sein kann. Stets gehören mindestens zwei abgehobene Inputs dazu, wobei der ankündigende Input (Glocke) vor der Belohnung (Nahrung) liegen sollte.
Wenn wir in Bezug auf Interferenznetzwerke über Lernen sprechen, so beschränken wir uns zum Zwecke der Allgemeinverständlichkeit auf elementarste Grundlagen. Als solche mögen Gewichtslernen (Weight Learning) und Verzögerungslernen (Delay-Learning) genügen.
Donald Hebb, ein Schüler von Karl Lashley und ein Kollege von Karl Pribram, formulierte eine erste, noch heute die ANN-Welt dominierende Lern-Hypothese ("Hebb's Rule"):
"When an axon of cell A is near enough to excite cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased."
Hebb, D.O.: The Organization of Behaviour. J. Willey & Sons, New York 1949
("Wenn ein Axon von Zelle A nahe genug ist, um Zelle B zu erregen, und wiederholt oder beharrlich daran beteiligt ist, sie zu befeuern, findet in einer oder beiden Zellen ein Wachstumsprozess oder eine Stoffwechselveränderung statt, so dass die Effizienz von A als eine der Zellen, die B befeuern, erhöht wird.")
Hebb's Rule soll für das Lernen von Gewichten gelten. Leider sagt Hebb nichts darüber aus, welcher biochemische Vorgang diesen Wachstumsprozeß auslösen könnte. Dem Autor ist in den Jahren seit dem Buch "Neuronale Interferenzen" (NI93) keine restlos schlüssige Erklärung begegnet.
Gilt Gewichtslernen auch für Interferenznetzwerke, in denen verzögerte Pulse interagieren - also für Nervennetze?
Über dynamische Adressierung oder eine Verzögerungsstruktur sagt Hebb's Rule nichts aus. Während die neuronale Netzwerkforschung (NN, ANN) vierzig Jahre lang Kartierungsprinzipien über Modifikation von Gewichten herleitete (alle, von Perzeptron bis zu SOM), können verzögernde Pulsnetzwerke ihre Kartierung nur auf der Verzögerungsstruktur des Netzwerks erzeugen. Aber:
Gewichte können der Adressierung durch Verzögerungen nicht widerstehen. Delays sind stärker als Gewichte.
So existiert für das Beispiel von Abb.2-1 keine Gewichtskonstellation, die die Zuordnung der Codemuster (Fall 1 oder Fall 2) zu den Neuronen umkehren kann!
Primär sind in einem verzögernden Pulsnetzwerk folglich Delay-Adressen vorhanden, nur auf diesen kann gelernt werden.
Gewichtslernen kann in verzögernden Netzwerken nur auf einer vorhandenen Verzögerungsstruktur erfolgen. Ist die Verzögerungsstruktur nicht vorhanden, kann nichts gelernt werden.
Das heißt: Werden Codes in ein Netzwerk gesendet, die im Netz keine Delay-Adressen besitzen, verpuffen die Codes. Nichts passiert.
Diese Erkenntnis bringt ein generelles Umdenken bei der Hebb'schen Regel mit sich.
Wenn wir unterstellen, daß bei einem zu einem Ziel wachsenden Neurit die Verzögerungszeit desselben mitwächst, stimmt die Verzögerungsstruktur nicht mehr, wenn der Neurit am Ziel ankommt, die Zieladresse ist dann unter Umständen falsch. Das bedeutet, daß erst ein Netzwerk mit (Delay-) Adressen vorhanden sein muß, ehe dort gelernt werden kann, wo eine Adresse bereits vorhanden ist.
Letztlich bedeutet sie, daß ein erster Prozeß der des Wachstum eines (wie auch immer gearteten) Nervenfilzes sein muß, und ein zweiter Prozeß der des (gewichteten) Lernens und zwar nur an den Orten, die bereits eine Adresse besitzen. Synapsen entstehen dann nur dort.
Existiert kein Adressort zu einem zeitlichen Muster, kann dieses Muster nicht erlernt werden, d.h. das IN reagiert nicht auf dieses Muster. (Unter Adresse wird das zeitliche Muster verstanden, welches einen Adressort erregen kann.)
Im Umkehrschluß könnte daraus entstehen:
Existiert kein zeitliches Muster zu einer Adresse, kann die Adresse nicht erlernt werden.
Das etwa wäre eine plausible, an Pulsinterferenzen angepaßte, modifizierte Hebb'sche Regel. Diese Auffassung entspricht Erkenntnissen der Individualgenese. Karl Pribram sandte mir ein Bild von Pomerat's Erkenntnissen.
(Fig.2-2, p.29 in Pribram, Karl: Languages of the Brain, 1971). Pomerat beobachtete 1964 ein filzartiges Aussprossen der Nervenenden (growth cones).
Nachdem Kontakte zu anderen Nervenzellen hergestellt sind, verkümmern ungenutzte Dendriten.
Download Karl Pribrams Buch als
PDF (17 MB).

Abb.3-2: Fig.2-2 von Pomerat aus Karl Pribram's Buch.
Pribram differenziert zwischen stochastischem, filzartigem Wachstum und synaptischer Generation/Degeneration. Synapsen werden nur dort verstärkt, wo sie gebraucht werden. Werden Sprossungen oder Synapsen nicht gebraucht, degenerieren sie wieder.
Nebenbei erwähnt Karl Pribram auf Seite 31 ein äußerst brisantes Detail:
"Since fiber diameter is often an indicator of the length of the fiber, the thickening indirectly suggests that growth may have taken place." p.31
Mit anderen Worten: Wird eine Nervenfaser länger, so wird sie gleichzeitig dicker. Dickenwachstum aber bedeutet: Sie wird schneller. Das kann nur eines bedeuten: Diese Faser versucht, ihr Delay, ihre Signalverzögerung zu erhalten!
Erinnern wir uns an das Wachstum unserer Kinder, so hatte der Wachstumsprozess Einschnitte zu verzeichnen. Abrupte Verhaltensänderungen traten auf. Waren dies die Punkte, an dem die Verzögerungsarchitektur mitwachsender Nervenfasern nicht mehr mithalten konnte und durcheinander kam?
Auch erhalten wir hier ein Kriterium zur Beurteilung der Leistungsfähigkeit neuronaler Lernalgorithmen. Passen Codemuster eines Algorithmus auf Verzögerungsadressen, ist dieser potentiell in der Lage, Nervennetze zu simulieren. Alle anderen Algorithmen haben mit Nervennetzen nicht viel zu tun, sie gehören ins Reich der "Artificial Neural Networks" (ANN).
Die selbstorganisierende Karte der Interferenznetze ist die Adressierung über Netzwerk- immanente Verzögerungen (Delays).
Da die Verzögerungsstruktur des Netzwerks aber räumlich fixiert ist, bedeutet dies eine dreidimensionale Bindung und eine gewisse Körperlichkeit. "Form kodiert Verhalten" schrieb der Autor im Vorwort zum Buch "Neuronale Interferenzen" (NI93) 1993:
Will das Netzwerk lernen, so ist vor dem Lernen von Gewichten zu prüfen, ob die erforderlichen Verzögerungsadressen auch vorhanden sind.
Dazu gibt es eine traurige Geschichte. 1990 fand man in rumänischen Kinderheimen zig tausende, völlig verwahrloste Kleinkinder von Ceaucescu-Opfern, die kaum Kontakt mit jemandem hatten. Kinder, die damals schon älter als zwei Jahre waren, werden lebenslang an chronischen Verhaltensdefiziten leiden. Offenbar bildet sich die Grundstruktur unseres Nervennetzes in den ersten zwei Jahren aus.
Weil der Adreßraum als Verzögerungsstruktur aus einer dreidimensionalen Körperlichkeit von verzögernden Leitbahnen resultiert, wird er sich nur in bescheidenem Rahmen an veränderte Muster anpassen. Denkbar sind Leitgeschwindigkeitsänderungen durch geringe Variation des Durchmessers oder der Länge einer Faser. Verändern sich Muster oder Netzwerk über Anpassungsgrenzen hinaus, verschwindet das Erlernte für immer, auch wenn erlernte Gewichte vollständig erhalten bleiben: Wissen, Koordination oder Verhalten sind plötzlich nicht mehr abrufbar.
Dieser Umstand gibt einen Hinweis auf eine Erkrankung, bei der die Myelinscheiden von Nerven degenerieren, und Nervenfasern damit drastisch langsamer werden. Bei der multiplen Sklerose (MS) gerät die Verzögerungsstruktur des Netzwerks durcheinander. Codes erreichen nicht mehr die eigentlich adressierten Neuronen. Sollte sich im Laufe einer Spontanheilung von MS zeigen, daß plötzlich wieder alles funktioniert, hieße das, daß die Gewichte die Krankheit überdauert hätten. Ob solche Fälle existieren, entzieht sich der Kenntnis des Autors.
Karl Lashley, damals der Chef von Donald Hebb und Karl Pribram im Yerkes Laboratory for Primate Biology in Florida, untersuchte Lernen mit Tierexperimenten. Auf der Suche nach dem Speicherort erlernten Verhaltens konnte er bei Ratten unterschiedliche Bereiche des Cortex entfernen, ohne eine erlernte Information (Weg durch ein Labyrint) zu zerstören. Nach 30 Jahren kam er ironisch zum Schluß, daß "die Experimente zeigten, daß die Speicherung des Erlernten nicht im Gehirn erfolgt". Als erster spricht Karl Lashley von Interferenzmustern. Karl Pribram schreibt in 'Brain and Mathematics' auf S.4:
"Lashley hatte vorgeschlagen, dass Interferenzmuster zwischen Wellenfronten in der elektrischen Aktivität des Gehirns auch als Substrat von Wahrnehmung und Gedächtnis dienen könnten. Das entsprach meinen früheren Intuitionen, aber Lashley und ich hatten diese Alternative wiederholt diskutiert, ohne auf eine Idee zu kommen, wie Wellenfronten im Gehirn aussehen könnten. Wir konnten auch nicht herausfinden, wie sie, wenn es sie gäbe, irgendetwas auf der Verhaltensebene erklären könnten. Die Diskussionen, die zwischen 1946 und 1948 stattfanden, wurden etwas unangenehm im Hinblick auf Donald Hebb's Buch ("The Organization of Behavior", 1949), das er zu der Zeit schrieb, als wir alle zusammen im Yerkes Laboratory for Primate Biology in Florida waren. Lashley mochte Hebbs Formulierung nicht, konnte aber seine Gründe für diese Meinung nicht ausdrücken: 'Hebb is correct in all his details, but he's just oh so wrong.'"
Heute wissen wir, daß ein Neuron nur dort aktiv werden kann, wo alle Partialwellen eines sendenden Neurons gleichzeitig ankommen.
"Delays dominate over weights"
schrieb ich in verschiedensten Aufsätzen. Gewichtslernen ohne Delays als Grundstock einer künstlich-neuronalen Netzwerktheorie (ANN) führt damit unweigerlich zu einem gegenüber dem Nervennetz völlig anderen Verhalten.
Lashley erahnte offenbar bereits die interferenzielle Blockade des Gewichtslernens durch Verzögerungsadressen. Möglicherweise ahnte er auch, daß Wellen-Interferenzen nur zu einer interferenziellen Art des Lernens führen können. Wie dem auch sei:
Hebb's Rule beschränkt sich auf Gewichtslernen und gilt damit nur auf einem Netzwerk mit bereits vorhandenen Verzögerungsadressen, oder für ein verzögerungsfreies Netzwerk. Dieses existiert aber nicht in der Natur, es existiert nur im Computer als ANN (Artificial Neural Network).
Oder mit den Worten von Karl Lashley: 'Hebb is correct in all his details, but he's just oh so wrong'.
Hebb's Rule führte damit direkt zu künstlich-neuronalen Netzen (ANN), deren Verhalten nichts mit dem von Nervennetzen zu tun hat. Mehr dazu siehe die Seite zum holografischen Gehirn.
Ein Problem bei Anwendung der Hebbschen Regel besteht darin, daß ANN mit im Nervensystem nicht vorhandenen Fernwirkungen arbeiten. Vom Algorithmus werden in unendlich kurzer Zeit Gewichte gesteuert, Delays spielen keine Rolle und wurden bereits 1943 von McCulloch/Pitts durch (Computer-) Takte ersetzt. Siehe dazu Details in
"McCulloch/Pitts leiteten eine Fehlentwicklung ein"
(german), (english).
Die entscheidende Frage ist die, woher lokale Informationen kommen können, die ein Neuron braucht, um ein Delay oder Gewicht eines bestimmten Pfades verändern zu können.
Woher könnten lokale Belohnungsanreize kommen?
Unendlich schnelle Fernwirkungen sind im Nervensystem nicht bekannt. Nervenleitgeschwindigkeiten sind sehr langsam, verglichen mit elektrischen Signalen. Im Gegensatz zum Computer können sie nicht ferngesteuert werden.
Genauso wichtig ist die von Hebb unbeantwortete Frage, wie Inhibition in Form hemmender Synapsen entstehen kann. Auch sie sind lokal zu initiieren.
Im Kap.14 werden wir uns der Erkennung von Tönen und Harmonien zuwenden. Dr. Friedrich Blutner hatte dazu eine substanzielle Anregung: Das Gehör von Berufsmusikern kann absolute Frequenzabweichungen von wenigen Hertz wahrnehmen, man spricht dabei vom "absoluten Gehör".
Da Frequenzen oder zeitliche Abläufe prinzipiell nur mit nervlichen Verzögerungszeiten erkennbar oder initiierbar sind, entsteht die Frage, wie eine Nervenzelle ein Delay so präzise abstimmen kann, daß solche Erkennungsleistungen möglich werden.
Analog sind Abläufe bei sportlichen Wettbewerben zu bewerten. Der Turmspringer, die Turnerin oder der Fußballspieler haben komplexe Aktionen auf die hunderstel Sekunde genau auszuführen. Je genauer der Sportler oder die Sportlerin das Timing beherrscht, je höher sind die Erfolgsaussichten.
Nun stellt sich die Frage, wie ein Neuron oder ein Teil eines Neurons (das Soma, ein Axon oder ein Dendrit) die Verzögerung durchlaufender Impulse abgleichen oder gezielt verändern kann. (Das dies prinzipiell möglich sein muß, beweisen uns alle erlernbaren, dynamischen Vorgänge, d.h. Sprechen oder Hören, Abläufe und Bewegungen oder Klang- Sprach- und Geräuschdetektionen aller Art.)
Neben einer Veränderung der Struktur durch Hebb's Rule ist dazu ein lokaler Regelungsprozeß nötig, der eine einzelne Verzögerung in Grenzen anpassen kann. Denken wir an die stark variierende Dicke - und damit an die Variation der Leitgeschwindigkeit verschiedener Axonen und an deren Fähigkeit, noch schneller zu leiten durch Myelinisierung, so steht diese Frage unmittelbar im Raum.
Denken wir an Neuronenmodellierungen in der Art von Hodgkin/Huxley, so kämen unzählige Parameter dafür in Betracht. Neben Ionenkonzentrationen insbesondere auch Länge und Dicke von Dendriten und Axon sowie Myelinisierung des Axons.
Woher also soll ein Dendrid oder ein Axon wissen, daß es langsamer oder schneller leiten soll? Woher soll es lokal wissen, ob eine hemmende oder eine anregende Synapse ausgebildet werden soll?
Im Bereich der Struktur des Netzwerkes steht eine Möglichkeit bereit. So wäre denkbar, daß eine (multipolare) Nervenzelle, deren Dendriten zufällig an andere Zellen ankoppeln, die häufig kohärent zueinander agieren, das Dickenwachstum der pulszuführenden Dendriten genau so steuert, das eine Impulsauslöschung (durch die Refraktärphase ankommender Impulse) im Soma stattfinden kann (analog zur Impulsauslöschung beim Ischias-Nerv). Sie würde dann immer feuern, wenn diese Nervenzellen zwar zeitlich versetzt, aber kohärent zueinander feuern.
Auf diese Weise könnten zuvor vollkommen unabhängige Vorgänge oder Prozesse miteinander verknüpft werden. Auch entsteht dadurch dynamische Plastizität, die Nervenzelle paßt sich kleinen Delay- Veränderungen an.
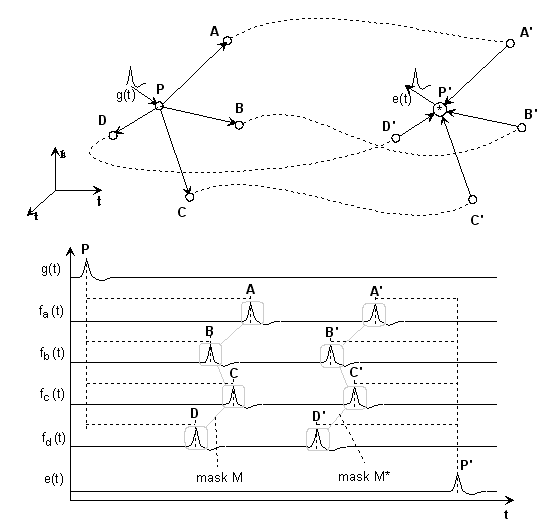
Abb.3-3: Maske M und komplementäre Maske M' eines einfachsten Interferenzkreises, bestehend aus zwei Neuronen (Maske M bezieht sich auf P, Maske M' auf P'). Ein Puls von Neuron P soll eine Erregung des Neuurons P' auslösen. Hätten beide Neuronen identische Topologie, wäre eine Pulsübertragung unmöglich. Quelle Kap.4 aus der Seite "Biomodelle"
Wenn wir annehmen, daß die Orte A und A' bis D und D' identisch sind, fällt auf, daß die entsprechenden Verzögerungszeiten sehr unterschiedlich ausfallen müssen. So sind Länge und Delay von PA ungleich P'A' und so weiter. Soll eine Kommunikation stattfinden, haben die Fasern unterschiedlich dick zu sein. Das Prinzip der Nachbarschaftshemmung
(Link) wird deutlich. Eng benachbarte Neuronen können dadurch i.a. nicht miteinander kommunizieren.
Hier betrachten wir nur die rechte Seite von Abb.3-2. Damit Neuron P' dann feuern kann, wenn P Pulse abgibt, hat die Maske M' von P' exakt gleich der komplementären (zeitinvertierten) Maske M von P zu sein.
Daraus läßt sich eine ausschließlich lokal realisierbare Regel ableiten, die keinerlei ominöse Fernwirkungen im Stil von ANN braucht. Die entstehende, lokale Regel zum Abgleich des Neurons P' auf optimale Delays würde lauten:
Ein Puls, der zeitlich verspätet zu den anderen ankommt, hätte ein Dickenwachstum oder eine Verkürzung des betreffenden Dendriten zu veranlassen. Hingegen hätte ein zeitlich verfrüht ankommender Puls auf dessen Dendrit eine Erhöhung des Delays oder eine Verlängerung durch Dickenabnahme zu veranlassen.
Zu beachten ist, daß diese Regel eine Überbestimmtheit des Wellenfelds voraussetzt, siehe dazu Kap.15.

Abb.3-4: Feinjustierung von Delays. An einer Synapse ankommende Pulse a) und b) kommen im Verhältnis zur Erregung des Neurons zu früh oder zu spät. Entsprechend hat sich das Delay des zugehörigen Dendrits zu verringern für Fall b) oder zu vergrößern für Fall a)
Die Verzögerung τ ist gleich der zurückgelegten Strecke s dividiert durch die Leitgeschwindigkeit v der Faser.
τ = s / v
Die Leitgeschwindigkeit des Dendriten wiederum nimmt mit dessen Dicke d zu. Das Delay τ des betreffenden Dendriten wird also mit dem Faserdurchmesser d abnehmen, konstante Länge s vorausgesetzt.
τ ∼ s / d
Es wäre ein biochemischer Vorgang anzunehmen, der bei verfrühtem oder verspätetem Eintreffen eines Impulses eine Dickenzunahme bzw. Dickenabnahme des Dendriten bewirkt.
Nun wissen wir, daß eine Nervenzelle von Milliarden Impulsen täglich befeuert wird. Eine einzelne Pulsgruppe darf also nichts ausrichten. Erst deren stete Wiederholung über Tage, Wochen oder Monate darf eine allmähliche Veränderung des Verhaltens bewirken können.
Ein Leistungssportler weiß, was das heißt: Nur stete Wiederholung derselben Trainingseinheit wird helfen, diesen dynamischen Feinabgleich zu vollenden und die Übung zur Perfektion zu bringen.
Das wäre aber nur der Anfang. Wir brauchen weiteres Wissen darüber, welche lokalen Mechanismen zu Erregung, Hemmung oder zu Delay-Abgleich führen können.
Und es bleibt eine entscheidende Frage offen: Wie ist es möglich, daß aus solchen lokalen Veränderungen sinnvolles Verhalten entsteht? Für die Klangwahrnehmung nach
Kap.14.2 wären entsprechende Verschaltungen denkbar.
Andrew Packard entdeckte 1995, daß eine interferentielle Erregungsausbreitung zwischen Chromatophoren (farbgebende Zellen) von Tintenfischen beobachtbar ist. Diese genügt einem einfachsten Interferenzmodell. Er beobachtete Farbwellen spontaner Erregung [AP1995].
Das besondere daran: Das Substrat besitzt eine nahezu homogene, konstante Ausbreitungsgeschwindigkeit, die Wellen ähneln Wasserwellen.
 Abb.4-1: Wellen spontaner Erregung auf einem Tintenfisch, bei dem das Rückenmark durchtrennt wurde
Abb.4-1: Wellen spontaner Erregung auf einem Tintenfisch, bei dem das Rückenmark durchtrennt wurde
Was wir auf dem Tintenfisch zu sehen glauben, sind Wellen. Was wir aber wirklich sehen, sind sich öffnende und schließende Chromatophoren. Was also macht unsere Wellenabstraktion aus?
Aus dem Physikunterricht kennen wir die eindimensionale, elementare Beschreibung einer Zeitfunktion z.B. in der Form
f(x-vt) (siehe Animationen).
Stellen wir uns viele solcher Zeitfunktionen vor, die in Maschen eines 3-dimensionalen Netzwerks fließen. Dessen Knoten mögen irgendwelche Verknüpfungen zwischen ankommenden Zeitfunktionen vornehmen (Addition, Multiplikation...) und sie weitersenden. Zurücksenden wird durch die Refraktärzeit verhindert, die Welle kann sich nur nach vorn ausbreiten.
Andrew konnte auch Wellen filmen, die aufeinander zulaufen. Sie verlöschen am Treffort ebenfalls durch deren Refraktärzeit.
Nehmen wir an, unser Netz sei in Ruhe und wir erregen einen einzigen Knoten mit einem Puls. Wenn wir herauszoomen aus diesem Netzwerk, können wir eine Pulsausbreitung in Form einer kugelähnlichen Welle beobachten, die sich um unseren Knoten herum ausbreitet. Beobachtbar wäre sie allerdings nur bei homogener Leitgeschwindigkeit, z.B. in der Akustik oder bei Andrews Squids. Im Falle inhomogener Leitgeschwindigkeiten und eines inhomogen gestalteten Netzwerks (Cortex) wird die Vorstellung schwieriger. Recht schnell wird der optische Eindruck von einer Kugelwelle dem eines Chaos weichen. Wie dem auch sei: Wir bemerken, daß die eindimensional bewegte Zeitfunktion im n-dimensionalen einer Welle gleicht - auch wenn wir dies bei Inhomogenität mit bloßem Auge nicht mehr erkennen können. Daher der Name: Wellen auf Leitbahnen.
Als 'Zeitfunktionswelle' bezeichen wir eine elementare Abstraktion der
zeitlichen Verschiebung einer Information (hier: Puls) in einem Netzwerk oder in einem Medium.
Netzwerke, deren Funktion durch Verzögerung der Informationsübertragung maßgeblich definiert wird, bezeichnen wir als Interferenznetzwerke.
Warum interessiert uns das? Weil 1993 entdeckt wurde, daß diese Interferenznetzwerke abbildende Eigenschaften besitzen. Damit stehen Andrews Tintenfisch- Experimente über das Hilfsmittel Interferenznetzwerk plötzlich in einer Reihe mit bekannten, spiegelverkehrten Abbildungen im Nervensystem (Homunculus; visueller Cortex etc.). Das eine bedingt das andere:
Wo eine Abbildung zu finden ist, ist Wellenausbreitung die Ursache; wo Wellenausbreitung zu finden ist, sind abbildende Projektionen zu erwarten.
Dieser Satz gilt übrigens auch für optische oder akustische Abbildungen.
Bedenken wir, daß eine einzige unterbrochene, elektrische Leitbahn im Auto dazu
führt, daß ein Betriebsmittel (Blinker, Scheinwerfer, Hupe, Radio...) nicht
mehr funktioniert, und bedenken wir weiterhin, daß eine Nervenzelle nur rund
sieben Jahre alt wird, wir hingegen durchschnittlich fünfundsiebzig, so wird
ein Problem offenbar. Mit fünfundsiebzig würde keine einzige Nervenverbindung
in unserem Körper mehr funktionieren. Weder würden wir die heisse Herdplatte
spüren, noch könnten wir die Hand wegnehmen.
Eine einfache 'Klingeldraht'- Verbindung zwischen Sensor/Aktor und Hirn können
wir uns folglich nicht leisten. Jede Nervenzelle braucht viele Double(s).
Vielleicht legen wir jede Leitung mehrfach? Oder wir löten alle Leitungen an allen Steckern zusammen? Fortan würden Scheinwerfer, Anlasser, Blinker, Scheibenheber und Hupe mit betätigt, wenn wir den Wischwasch-Schalter betätigen.
Oder repariert sich die defekte
Leitung selbst?
Im Prinzip wäre das möglich. Wäre da nicht das Lernen von notwendigen Kreuz-
und Querverschaltungen: Muskeln sollen gespannt werden beim Aufstehen, andere
sollen gespannt werden beim Hinsetzen, wieder andere sollen beim Aufstehen und
beim Hinsetzen entspannt werden. Das biologische Netzwerk ist millionenfach
kreuz- und querverschaltet.
Wenn wir also auf den einzelnen Klingeldraht verzichten müssen - wie bekommen
wir in einem chaotisch verschalteten, überall kurzgeschlossenen Netzwerk aus
Neuronen auch nur eine einzige Information "Bitte mal beugen!" fünfundsiebzig
Jahre lang an dieselbe Adresse (rechter Zeigefinger)?
Ein Neuron besitzt keine IP-Adresse. Der Natur steht kein Protokoll zur
Verfügung, mit dem eine Information gezielt zu einem Ziel gesendet werden kann.
Auch ist dem Absender i.a. unklar, welches Ziel die Daten erreichen sollen,
wenn neuronale Lernfähigkeit an verschiedensten Stellen des Netzwerks möglich
sein soll.
Wie also könnte eine Lösung beschaffen sein?
In einem kreuz- und quer verschalteten (überall kurzgeschlossenenen) Netzwerk
können offenbar nur Signallaufzeiten Quelle und Ziel einer Information verbinden - über Interferenzintegrale.
Dazu haben wir jede Information (Pulswelle) in alle Richtungen auszusenden. Dort, wo
zufällig mehrere Pulse eines Absenders wieder gleichzeitig
ankommen (umgangssprachlich: interferieren), entsteht ein höherer Effektivwert
- das Ziel ist erreicht [NI93] .
Dies können auch gleichzeitig mehrere Ziele sein. Oder hintereinander gestaffelte Ziele. Im Unterschied zum WWW können Herkunfts-
und Zieladresse von Information in Nervennetzen nur über die Geometrie des
(inhomogenen) Laufzeitraumes definiert werden.
Als 'Weichen' können alle verzögerungsändernden Einheiten betrachtet werden:
Gliapotential, chem. Botenstoffe, synaptische Stärke (diese verändert die
Zeitkonstanten), gehemmte oder erregte Nervenzellen als Umwegleitungen, Dehnung
und Stauchung von Fasern (siehe Daumenexperiment).
In Konsequenz entsteht daraus eine neue Informatik: Im
Gegensatz zum Internet-PC weiß die Nervenzelle nicht, an wen und wohin sie Ihre
Daten sendet. Selbst wir können es nicht beobachten, da jede Information
zunächst in alle Richtungen entschwindet - aber nur an wenigen Orten wieder
positiv mit sich selbst interferiert.
Haben wir auch nur eine leise
Vorstellung, was es bedeutet, eine solche Informatik zu verstehen? Erst wenn
diese interferenzielle Informatik hinreichend validiert ist, sollten wir an
Deutungen von Bewußtsein oder Intuition herangehen. Alles andere ist Scharlatanerie.
Als 1993 die Idee geboren wurde, siehe Jahresberichte oder Projekt-Directory,
war zunächst noch unsicher, ob die Betrachtungsweisen stimmen. Die Simulation eines Wellenfeldes im Kopf übersteigt i.a. unser Vorstellungsvermögen. Es mußten einfache
Nachweisexperimente entwickelt werden. So entstand die Idee, einen einfachsten Simulator zu
schreiben, der einige, wesentliche Eigenschaften von Interferenznetzen simulieren kann (PSI-Tools ganz am Ende dieser
Seite).
Wir nahmen gedanklich eine Bitmap mit schwarzen Pixeln, taten so, als ob die
Bitmap ein quadratischer Teich ohne Rand und die Pixel in den Teich geworfene
Steine wären und senkten drei Sensoren (grün) hinein, die die Wellenbewegung
der Teichoberfläche als Zeitfunktion aufnehmen. Daraus entstehen dann drei
Zeitfunktionen, siehe zweites Bild. Die erste Frage war nun: Beinhalten diese Zeitfunktionen tatsächlich das Bild der Bitmap? Kann man das Generatorbild aus den aufgezeichneten Zeitfunktionen wieder herauslesen? Und unter welchen Einschränkungen ist dies möglich?
5.1 Generatorfeld

Abb.5-1: Bitmap als Generatorfeld. Schwarze Pixel pulsen
An den Stellen der schwarzen Pixel mögen nacheinander Steine in einen Teich geworfen werden. Wellen breiten sich kreisförmig um die Emissionsorte herum aus, und erreichen schließlich die grün dargestellten Sensoren. An den drei grün markierten Sensor-Orten mögen die Zeitfunktionen des Wellenfeldes aufgenommen werden.
5.2 Zeitfunktionen (3 Kanäle)

Abb.5-2: Entstandene Zeitfunktionen der Bitmap für die drei Sensor-Orte (die Zeitachse zeigt nach rechts).
Man erkennt verschiedene Zeitfunktionen (blau,
grün und rot), die Spikes zu verschiedenen Zeitpunkten aufweisen. Die
Pulsabbildung soll in drei Kanälen (wir denken an Axonen) übertragen werden.
Rekonstruktives Interferenzintegral
Folgend werden die Zeitfunktionen an definierten Orten (schwarz) in einen
zweiten (Wellen-) Teich geleitet. (Im Falle der Interferenz-Rekonstruktion im
Prinzip zeitlich rückwärts). Allerdings wurden dessen x-, y- Koordinaten der
Einspeiseorte leicht verschieden zu denen des Sensorfeldes gewählt. Die
Laufzeit auf den drei Leitbahnen wird hier als identisch angenommen
(gleichlang, null). Nun interferieren die Pulse an den ursprünglichen
Quellorten mit sich selbst (wir nennen dies Eigeninterferenz) aber auch
mit Vorgängern und Nachfolgern
(Fremdinterferenz, Cross-Interference, Aliasing). Die Selbstinterferenz erzeugt
ein Interferenzintegral in Form des "GH". Fremdinterferenzen erzeugen die am
Rand sichtbaren, zusätzlichen Emissionen.
Der Computer gestattet uns die Wahl der Zeitrichtung für die Berechnung des
Interferenzintegrals. Wollen wir in die Kanäle testweise sozusagen von hinten
hineinschauen, wählen wir vom Ansatz her rückwärtslaufende Zeit oder negative
Delays und erhalten eine sog.
Interferenz-Rekonstruktion. Interessieren wir uns für
eine in einem Nervennetz tatsächlich stattfindende Abbildung, wählen wir
vorwärtslaufende Zeit und erhalten eine sog.
Interferenzprojektion.
Rekonstruktion und Projektion sind bei sonst gleichen Parametern genau
spiegelverkehrt zueinander, d.h. die Rekonstruktion erscheint seitenrichtig zum
Original, die Projektion hingegen spiegelverkehrt (siehe auch weiter
unten). Dabei kennt die Natur nur die (spiegelverkehrte) Projektion, die (seitenrichtige) Rekonstruktion braucht zwingend den Computer.
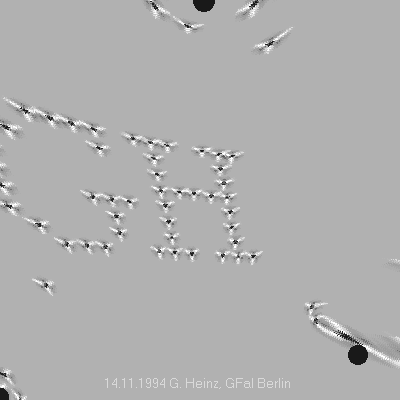
Abb.5-3: Dreikanaliges Interferenzintegral aus den Kanaldaten vom 14.11.1994 - historisch eine der ersten, gelungenen Interferenzrekonstruktionen (Bio-Interface, später umbenannt in PSI-Tools,). Der Quellort rechts unten wurde verschoben, damit wird das ursprüngliche Bild verzerrt wiedergegeben.
Die Koordinaten des rechten Kanals in Abb.5-3 wurden aus der rechten, unteren Ecke nach oben/innen verschoben, um nachzusehen, wie das Interferenzintegral reagiert. Es mangelte einfach an Phantasie, sich vorzustellen, wie ein simples Integral bei Verzerrung der Quellgeometrie reagiert.
Damals bestand eine gewaltige Herausforderung in der Rechenzeit: Diese Bildberechnung benötigte etwa ein Wochenende, erste Movies brauchten eine Woche. Hatte man falsche Parameter für Belichtung oder Rekonstruktion gewählt, begann alles nochmal von vorn.
Ein örtlich vom Senderaum verschiedener Empfangsraum kann benutzt werden, um
die Überlagerung von Impulsen (Interferenz) in Zielräumen abweichender
Geometrie zu prüfen. Eine Integration über die Erregung jedes Ortes
(Interferenzintegral) hält die zu verschiedenen Zeiten erfolgten Interferenzen im Bild fest. Die Simulation zeigt, unter welchen Bedingungen ein Empfänger aus mehrfach-parallel übertragenen Kanaldaten die Sendeorte (Sendeadressen) z.B. sensorischer Erregungen rekonstruieren kann. Im Bild wurde die rechte, untere Elektrode um 10% in das dem Generatorfeld gleichende Empfangsfeld hineingeschoben, bevor die Rekonstruktion gestartet wurde, das Interferenzbild erscheint nach links oben verzerrt.
Wie zu erahnen, lehnen sich diese Fragen an solche an, die beim GPS (Global
Positioning System), bei Phased Arrays bei SONAR oder RADAR stehen oder an
die Fragen, die von den Kollegen des SKA (Square Kilometer Array) oder bei Sonographiegeräten zu beantworten waren. Auch hierbei handelt es sich um
vergleichbar einfache Interferenzsysteme technischer Art.
Nach Irritationen mit der Theorie der sog. Neural Nets (NN) grenzte ich die Forschungen zu (Pulswellen-) Netzwerken gegen 1997 als "Interferenznetzwerke (IN)" ab. Ursache waren permanente Mißverständnisse bei Vorträgen oder Veröffentlichungen. Man konnte weder den Ansatz, noch die Aussagen zur IN-Theorie nachvollziehen, da kein entsprechendes Wissen vorhanden war. Bis heute werden Interferenznetzwerke nirgens gelehrt. Meine Versuche, entsprechende Vorlesungen an Instituten der Humboldt-Universität in Berlin einzurichten, gingen leider ins Leere. Man verstand weder Motivation, noch Inhalt der Theorie.
Da man in der Neurogemeinde aber wohl registrierte,
daß übliche Ansätze (mit Zustandsautomaten und verzögerungsfreien Leitbahnen etc.) für die Beschreibung von Nervennetzen offenbar vollkommen ungeeignet sind, ging man folgend mehr und mehr dazu über, das klassische Forschungsfeld "Neuronale Netze" (NN) als "Artifical Neural Nets" (ANN) zu bezeichnen.
Dieser Entwicklung verdanken wir das Kuriosum, daß wir die Netzwerke, die sich mit der Modellierung nervlicher Eigenschaften befassen, als Interferenznetzwerke bezeichenen müssen, während laufzeitfreie, "künstliche neuronale Netzwerke" (ANN) - vor allem in den Jahren bis 1997 - als "Neuronale Netzwerke" bezeichnet wurden.
Noch heute ist die Irritation für die studentische Ausbildung fatal. Man schlage ein beliebiges Buch zu Neuronalen Netzwerken auf: In der Einleitung findet sich die Biologie der Nervenzellen, darauf folgen die Theorien der künstlich neuronalen Netze - die mit Nervennetzen meist keine Gemeinsamkeit im Verhalten besitzen können.
Überleben im Tierreich ist unmittelbar mit dem Begriff des Wiedererkennens
verbunden, man denke an Wege zu Nahrungs- oder Wasserstellen, die optische
Unterscheidung zwischen Giftpflanze und Nahrung, zwischen Felsklippe und Stufe, zwischen Freund und Feind,
zwischen groß und klein. Wiederzuerkennende, optische Merkmale aber sind
Abstandsänderungen und daraus folgend ständiger Größen- und Formänderung
unterzogen.
Versucht man nun, ein irgendwie gewichtetes Netzwerk mit einem Gesicht im
Abstand von einem Meter zur aufnehmenden Kamera zu trainieren, so wird dieses
Netz unter günstigen Umständen das Gesicht im selben
Abstand wiedererkennen. Die Wiedererkennung wird unmöglich sein, sobald wir den
Abstand zum Gesicht ändern, es drehen, es verschieben oder kippen.
Wie können wir ein Nervennetz überzeugen, ein Gesicht zu erkennen, das in
variierenden Abständen auftaucht? Wie könnte sich die Natur behelfen?
Dazu erinnern wir uns, daß die geometrische Wellenlänge
L = vT = v/f
(v: Leitgeschwindigkeit, T: Pausendauer, f = 1/T)
von der Leitgeschwindigkeit abhängt. Variiert die Leitgeschwindigkeit,
variieren die Interferenzorte. Was bedeutet das aber in einem abbildenden
Netzwerk? Wie kann man sich diese Variation vorstellen?
Dazu wollen wir einen ähnlichen Versuch wie oben machen. Als Generator dienen
G-förmig angeordnete Pulsgeneratoren (z.B. Neuronen).
Wieder mögen sich die Wellen um den
Quellort herum kreisförmig ausbreiten und zu unterschiedlichen Zeiten die drei
Kanäle erreichen. Über die Kanäle wird diesmal mit vorwärtslaufender Zeit in
das Empfangsfeld hineinprojiziert. Im Zielfeld angekommen, breiten sich auch hier die Wellen wieder kreisförmig
aus. Dort, wo sie sich treffen, färbt sich unser Bildschirm von gelb über rot
nach blau. Wir variieren hier nur die Ausbreitungsgeschwindigkeit der Wellen im
Empfangsfeld (Hintergrundgeschwindigkeit v).
Im Ergebnis erkennen wir, daß abhängig von der gewählten
Ausbreitungsgeschwindigkeit der Wellen im Empfangsraum unterschiedlich
ausgedehnte Interferenzintegrale ("Bilder") entstehen. Beim Fotoobjektiv nennt man diesen Effekt "Zoom".

Abb.6-1: Simulation einer Interferenzprojektion zwischen zwei neuronalen Feldern, die über drei Axone verbunden sind. Die Leitungsgeschwindigkeit v des Detektorfeldes wird variiert. First publications in:
(Virex96) Fig.8 and
(Bionet96) Fig.9.
Das Bild zeigt einen 'Zoom'-Effekt, der mit dem optischen Zoom vergleichbar ist. Je weiter wir herauszoomen, desto mehr Fremdinterferenzen kommen ins Feld. In Abbildung g) sehen wir holographische Eigenschaften und die Nichtlokalität des neuronalen Gedächtnisses (bekannt aus Lashleys Rattenexperimenten).
Die Zeitfunktionen
werden in einem Generatorraum mit einer normierten Geschwindigkeit v = 50 (z.B.
mm/sec) generiert. In einem zweiten, empfangenden Raum wird die Projektion
berechnet. Die Bildgröße variiert unter dem Einfluß der (normierten)
Leitgeschwindigkeit (v = 100, 75, 50, 20, 10) im Empfangsraum. a) Simuliertes
Generatorfeld, schwarze Pixel pulsen; b) resultierende Kanaldaten; c) bis e)
Interferenzintegrale über die Kanaldaten, Parameter ist die
Hintergrundgeschwindigkeit v. Wird eine zum Sender a) identische
Geschwindigkeit benutzt, entsteht eine spiegelverkehrte Abbildung im gleichen
Maßstab d). Wird die Hintergrundgeschwindigkeit dagegen verändert, 'zoomt' das
Bild, vgl. c) und e). Interferenz entsteht dort im Empfangsraum, wo die
Pulswellen aller drei Kanäle gleichzeitig eintreffen. Werden die Koordinaten
z.B. in cm angenommen, ergibt sich die Geschwindigkeit in cm pro s (Pulsbreite 2ms, Abtastrate 5kHz). Die Erstveröffentlichung dieses Bildes erfolgte hier:
(Virex),
(Bionet96).
Erste Simulationen siehe GFaI-Jahresbericht
1994.
Nun werden Sie sich vielleicht fragen, wozu wir den ganzen Aufwand betrieben haben?
Dazu erinnern wir uns an die (Neuro-) Glia als Versorgungssubstrat der
Nervenzellen. Es ist bekannt, daß die Glia die Leitgeschwindigkeit von hindurchlaufenden Nervenfasern
beeinflußt. Wahrnehmen können wir dies über elektrostatische Ableitungen: Mit
Veränderung der Leitgeschwindigkeit verändert sich gleichzeitig das meßbare
Potential der Glia. Wenn wir also mit dem EEG (ECoG) Potentiale am Cortex
messen, so können wir annehmen, daß unterschiedliche Potentialregionen
unterschiedliche Leitgeschwindigkeiten aufweisen - nicht mehr und nicht weniger
(siehe dazu auch die
Seite der EEG-Experimente
). Da bereits im Buch "Neuronale Interferenzen" (1993) darauf hingewiesen wurde, daß eine Variation der Leitgeschwindigkeit im Sende-
oder Empfangsfeld den Maßstab der Abbildung zwischen beiden beeinflußt, lag es
nahe, ein Szenario für diese Simulation zu entwickeln.
Was wir hier vor uns sehen, ist nicht mehr und nicht weniger als die Wirkung
eines Potentialfeldes im EEG: Die Bilder darunter beginnen zu zoomen. Und der
Gradient am Rand könnte sogar noch für Versatz sorgen (siehe
Movement
).
EEGs haben folglich nichts mit nervlichen Daten zu tun. Wir sehen in Ihnen
Fokussierpotentiale für Abbildungen zwischen neuronalen Feldern, deren
technische Verwertung zur Defokussierung (Entgleisen) des Gesamtsystems führen könnte. (Diese Erkenntnis stoppte übrigens 1997 eigene Ideen für technische Applikationen von EEG.)
Erinnert sei aber auch, daß bestimmte Tintenfische möglicherweise nicht die Chance haben, zu zoomen. Sie erkennen Beutetiere nur dann wieder, wenn diese in der richtigen Entfernung vor ihnen auftauchen. Vielleicht aber haben sie gelernt, wann ein Angriff lohnt?
(Hinweis: Zu diesem Abschnitt existiert eine weiterführende Ergänzung in
deutsch und
english)
Lashley war auf der Suche nach dem Ort von Gedächtnisinhalten. Er trainierte
dazu Ratten, Nahrung in einem Labyrint zu finden. Dann entfernte er im Raster
systematisch kleine Teile des Gehirns und beobachtete die Wirkung. Gleich
welchen Teil des Cortex er entfernte, die Ratten erinnerten sich mehr oder
minder gut an das Erlernte.
Resigniert gestand er nach 30 Jahren, daß er nicht mehr sicher wäre, ob das Gehirn wirklich der Ort des Gedächtnisses sei: "The series of experiments ... has discovered nothing directly of the real nature of the engram"
(K.S. Lashley: "In search of the engram". Cambridge Univ. Press 1950, Ch.5, p.62).
Und doch hatte Lashley mit seinen Rattenexperimenten etwas entscheidendes entdeckt: Offenbar können Erinnerungen im Cortex nur holographisch codiert werden. Sehen wir uns dazu das folgende Bild an:

Abb.7-1: Simulation einer Dreikanalprojektion in einem zweidimensionalen Raum. Ausgehend von den drei "Axonen" K1...K3 fließen die Zeitfunktionen (Pulswellen) über das Feld. Überall dort, wo Impulse aufeinandertreffen, ist der Interferenzintegralwert höher, wir sehen kleine rote Spitzen als potenzielle Speicherorte.
Vereinfachend wird hier davon ausgegangen, dass sich die Pulswellen mit konstanter Geschwindigkeit bewegen - die Simulation zeigt lediglich das allgemeine Prinzip der Verzögerung durch Leitbahnen, das kortikale Hologramme produziert.
Wir finden holographische Eigenschaften und die Nichtlokalität des neuronalen Gedächtnisses (bekannt aus Lashleys Rattenexperimenten). Um das zentrale, selbstinterferenzielle "G" herum finden wir die Fremdinterferenzfiguren. Sie enthalten Teile des Zentralbildes "G". Die Pixel des "G" wurden relativ dicht immer wieder nacheinander gesendet.
Hinweise auf holographische Organisationsmöglichkeiten gaben seit den 50er
Jahren David Bohm und Karl Pribram. Dessen Schüler Walter Freeman gab
1972 in seinem Werk: Waves, Pulses, and the Theory of Neural Masses (Progress in theor. Biology, Vol. 2, 1972, New York/London)
sogar ein fiktives Bild eines Wellenfeldes an.
Der Zufall wollte es, das bei ersten Experimenten mit zoomenden Abbildungen sofort selbstholografische Kartierungen sichtbar wurden, siehe
Abb.6-1, g) oder den GFaI-Jahresbericht 1994, Bild 4,
(PDF).
Holografie liegt in der Natur der Interferenznetzwerke.
In Abb.6-1, g) erkennt man, daß nicht nur das Bild der Vorlage, ein großes "G", spiegelverkehrt im Bildraum entsteht, sondern viele, unvollständige "G" kartieren zusätzlich außen herum. Die Erkenntnis: Eine neuronale Karte kann nicht nur an einem Ort gespeichert werden. Sie wird immer gleichsam holografisch gespeichert.
Allerdings kartieren nur niederkanalige Projektionen direkt holografisch
(d = k+1). Eine zur Raumdimension d zu hohe Kanalzahl k beseitigt die Fremdinterferenzen (deshalb sind bei akustischen Kameras hohe Kanalzahlen erforderlich). Aber jede Projektion mit hoher Kanalzahl verursacht auch Projektionen mit niedriger Kanalzahl, daher sind alle neuronalen Projektionen holografisch.
Eine Vorhersage dafür gab es im Buch 'Neuronale Interferenzen' 1993, aber ohne simulativen Nachweis war diese nicht anschaulich. Da der Holographiebegriff für sinusförmige Zeitfunktionen optischer Art mit Referenzwellen in spezifischer Weise besetzt war, wurde die hier dargestellte Eigenschaft in [NI93] , Kap.5 als tutographische
Abbildung** - tuto : sicher, geschützt bezeichnet.
Holographie oder Tutographie?
Als Dénes Gábor in den vierzigern die Holographie erfand, entstand diese im Farbraum des Lichts, im Fourierraum. Wenden wir die Fouriertransformation aber auf pulsförmige Zeitfunktionen an, kommt nichts Gescheites dabei heraus.
Zu beachten wäre, daß der Begriff der interferenziellen Tutographie offen ist für jegliche Art von Zeitfunktionen (Dirac bis Sinus, Codemuster oder Zustandsfolge), während Holographie stets mit sinoidalen Zeitfunktionen assoziiert, man denke an das bekannte Lichtspektrum.
Damit wäre die (interferenzielle) Tutographie als Oberbegriff zur Holographie anzusehen, die auch im Zeitbereich erklärt ist.
Betrachten wir nochmals Abbildung Abb.6-1, g). Während in Bildern (c) bis (e)
nur ein spiegelverkehrtes 'G' zu erkennen ist, kommen in den Bildern (f) und
(g) weitere Interferenzen in das Bildfeld hinein. Offenbar interferieren nun
folgende Pulswellen miteinander und mit der jeweils originalen Pulswelle. Das
Ergebnis ist faszinierend. Wir finden dieselben Interferenzintegrale des 'G'
rundherum wieder! Abb.6-1, g) zeigt folglich eine Art von Hologramm als
fundamentale Eigenheit interferenzieller Abbildungen.
Plötzlich werden Lashleys Rattenexperimente interpretierbar:
Interferenznetze speichern holographisch (besser: tutografisch), und Lashley erbrachte den entscheidenden
Nachweis dafür!
Lashleys mißglückte Suche wird damit zu einem wichtigen Beweis für universelle, interferenzielle Wirkung im Nervensystem.
Die Neuroforscher Lashley, Pribram und Hebb hatten Gábor's Idee der Holographie bemerkt.
Als Karl Pribram Jahre später Dénes Gábor auf einer UNESCO-Konferenz kennenlernt, erklärt er diesem seine holographische Hirn- Analogie. Er schreibt dazu in "Brain and Mathematics" 1971:
"Gabor was pleased in general but stated that "brain processing [of the kind we were discussing] was Fourier-like but not exactly Fourier." I asked, what then might such a relation look like and Gabor had no answer."
Interessant daran ist die Wendung "but not exactly Fourier".
Gabor ahnt oder weiß offenbar, daß eine Fouriertransformation von stochastischen Pulsmustern keine sinnvollen Ergebnisse erbringen kann. Aber alle Holographie findet zu der Zeit im Spektralraum statt. Holographie im Zeitbereich existiert nicht ansatzweise, Abb.6-1, g) entstand erst 1995). Was Gabor also ausdrücken wollte, hieß etwa: Fourier und Holographie passen zur Optik, nicht aber zum Nervensystem. Um den Zusammenhang besser zu verstehen, erinnere man sich daran, daß das Spektrum des Lichts - dessen Fouriertransformierte - mit einem einfachen Prisma erzeugt werden kann.
Sehen wir uns das Ergebnis der Simulation näher an, so erkennen wir, daß durch
Pulsprojektionen nicht nur ein "G" auf ein "G" abgebildet wird. Vielmehr
erscheinen rund um ein zentrales "G" viele weitere "G". Die ursprünglich
einmalige Information "G" im Generatorfeld wird mehrfach in das Detektorfeld
abgebildet - aber warum?
Erinnern wir uns dazu der zwei möglichen Arten von Interferenzen:
1) Zum einen können identische Wellen des Pixels p miteinander interferieren
(Wellen/Zeitpunkte i,i,i). Dies betont den Ort der Selbstinterferenz,
den Ort des erwünschten "Abbildes" aller Pixel - unser gespiegeltes G in der
Bildmitte.
2) Daneben aber interferieren irgendwo im Laufzeitraum alle Wellen (i, i+1, i-1,
i+2, i-2 ...) aller Kanäle in Fremdinterferenz miteinander.
Trifft z.B. die i-te Welle von Kanal 1 auf die (i+1)-te Welle von
Kanal 2 und die (i-1)-te Welle von Kanal 3, so ensteht eine der Figuren
des innersten Kreises. Entstehende Interferenzmuster erscheinen ähnlich dem
Original. Andere Kombinationen bewirken die weiteren Fremdinterferenz-Figuren.
Das "G" wird folglich unvermeidbar nicht nur einmal, sondern vielfach in den
Detektorraum projiziert. Als Maß des Abstands zwischen Eigeninterferenz- und
Fremdinterferenz-Abbildern erkennen wir den (durchschnittlichen) Pulsabstand in
den Zeitfunktionen [NI93] und die darauf basierende Wellenlänge der Pulspause
oder den Fremdinterferenzradius R.
Wodurch wird nun eigentlich der Abstand R zwischen den wiederkehrenden 'G' in Abb.7-1 definiert? Dazu erinnern wir uns, daß sich im Interferenzintegral nur Orte
mit hohem Effektivwert abheben. Das sind genau die Orte, an denen sich Wellen
treffen.

Abb.8-1: Trifft eine Pulswelle an einem definierten Ort auf ihren eigenen Zwillingsbruder (umgangssprachlich auf sich selbst), so sprechen wir von Selbstinterferenz (a). Trifft sie hingegen auf einen Vorgänger oder Nachfolger, so sprechen wir von Fremdinterferenz (b). Bildquelle [NI93], Kap.2a, S.52
Bei der Selbst- oder Eigeninterferenz geht es im Kern entfernt um Kreuzkorrelation einer Zeitfunktion mit sich selbst. Bei Fremdinterferenzen könnte man entfernt an Autokorrelation denken.
Genau hier unterscheiden sich "Hören" und "Sehen" fundamental: Abbildende Projektionen (bildliche Vorstellungen) sind Selbstinterferenzabbildungen (a), während zeitliche Strukturen (Tonhöhe, Klänge, Sprache etc.) nur über Fremdinterferenzen (b) abgebildet werden können.
Betrachten wir aber Beziehungen innerhalb von Bildern (Texturen, Muster, Zugehörigkeiten), dann sind wir bei Fremdinterferenzen: Wir erkennen einen Gegenstand auch über Freminterferenz wieder! Sehen ist also auch Hören.
Damit aber ein Ort einen höheren Effektivwert bekommen kann, als jeder
benachbarte, ist dafür Sorge zu tragen, daß sich genau am Ort möglichst
viele Wellen aus unterschiedlichen Richtungen treffen.
Nun hat aber jede Welle einen Vorgänger und einen Nachfolger. Wenn sich also
viele Wellen an einem Ort treffen, dann befinden sich deren Vorgänger und
Nachfolger ebenfalls an wohldefinierten Orten - kurz davor oder kurz danach.
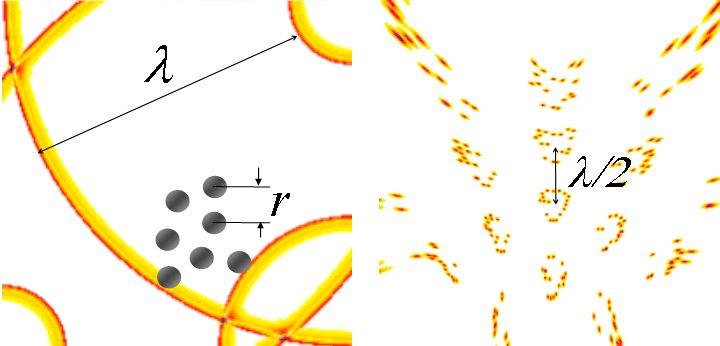
Abb.8-2: Trefforte von Wellen korrespondieren im Interferenzintegral mit Erregungsorten. Folglich kann der
Fremdinterferenzradius aus dem Wellenfeld ermittelt werden. Er ergibt sich aus dem durchschnittlichen Abstand aufeinanderfolgender Wellen, der mittleren Wellenlänge λ = 2R. (Pardon: Links ist ein 4-Kanal-Wellenfeld zu sehen, während rechts ein 3-Kanal Interferenzintegral zu sehen ist).
Zwischen der durchschnittlichen Puls-Pause T der Zeitfunktionen bei
(maximaler) Feuerrate f und dem Mittenabstand der Interferenzorte
(Fremdinterferenzradius) R existiert nun ein wunderbar einfacher
Zusammenhang.
Sei die Wellenlänge λ = vT mit v: Leitgeschwindigkeit und, T: Pulsabstand, so
interferieren gegenläufige Wellen jeweils auf der halben geometrischen
Wellenlänge wieder miteinander. Folglich besteht zwischen
durchschnittlicher Wellenlänge λ und Fremdinterferenzradius R der Zusammenhang [NI93]:
(1) R = λ/2 = vT/2
Mit einer Feuerrate f = 1/T
gilt
(2) R = v/2f
oder, wenn wir aus einer Faserdichte die zu erwartende Leitgeschwindigkeit
bestimmen wollen
(3) v = 2f R = 2f λ/2 = f λ.
In einem Interferenznetzwerk hängen die Größen Leitgeschwindigkeit v,
Fremdinterferenzradius R und Feuerrate f bzw.
Pulspause T = 1/f offenbar untrennbar zusammen. Besitzt ein
System einen z.B. durch Somatotopie vorgegebenen Fremdinterferenzradius, so
gehört dazu eine wohldefinierte Leitgeschwindigkeit. Gelingt es, eine Leitgeschwindigkeit zu messen, so läßt sich daraus die Größe des
somatotopischen Areals abschätzen.
Allerdings ist zu beachten, daß die Partialimpulse i.a. auf Fasern unterschiedlicher Dicke eintreffen. Dickenproportional variiert die Leitgeschwindigkeit stark. Insofern sind obige Formel nur Näherungen für eine gemittelte Leitgeschwindigkeit.
Ein Rechenbeispiel: Der Schweizer Gardist
Wollen wir eine Bewegung im kleinen Zeh auslösen, dann müssen Fremdinterferenzen auf dem Weg vom Cortex zum Zeh ausgeschlossen werden, sollen nicht andere Körperbereiche ebenfalls erregt werden.
Wie hoch müßte nun die Leitgeschwindigkeit v sein, damit zu adressierende Orte in unserem Körper nicht durch Fremdinterferenz überlagert werden? Wir nehmen an, das betrachtete Nervennetz möge eine maximale Feuerfrequenz f von 30 Hz haben, und das Individuum sei knapp zwei Meter groß (Schweizer Gardist) - damit haben wir einen Fremdinterferenzabstand R von etwa 2 Metern herzustellen. Und zwar sowohl für aufsteigende, als auch für absteigende Impulse.
R = 2m
mit R = λ/2 folgt
λ = 2R = 4m,
daraus folgt dann eine erforderliche Leitgeschwindigkeit v von
v = f · 2R = 30Hz · 4m = 120 m/s.
Sehen wir uns bekannte
Faserleitgeschwindigkeiten an, so entspräche dies einem Typ "Aa" nach Erlanger/Gasser oder Typ "I" nach Lloyd/Hunt.
Es handelt sich dabei um den schnellsten Fasertyp, dieser ist myelinisiert.
Sollten wir bemerken, daß Beispiele dieser Homepage auf bekannte Meßwerte aus dem Nervensystem passen: Kann das ein Zufall sein? Wohl eher nicht?
Diskussion
-
Wächst die Pulspause an, so wird der Fremdinterferenzabstand größer, größere
Gebiete können eindeutig addressiert werden.
-
Wird die Feuerrate höher, so wird der Fremdinterferenzabstand kleiner (siehe
Schmerzsimulation), die Abbildungen verwaschen.
-
Wird die Leitgeschwindigkeit höher, so wird der Fremdinterferenzabstand
größer, größere Gebiete können addressiert werden.
-
Wird die Leitgeschwindigkeit geringer, so wird das addressierbare Grid
feiner, mehr Information kann pro Volumeneinheit untergebracht werden (siehe
Speicherdichte).
Wichtig ist es, hier festzuhalten, daß Fremdinterferenz wie Selbstinterferenz eigenständige Aufgaben zu erfüllen haben und daß sie sich je nach Aufgabe ergänzen oder ausschließen.
Mehr dazu siehe
[NI93]
sowie spätere Publikationen im
Publikationsverzeichnis.
Der Bildinhalt steht bei Interferenzintegralen immer in Relation zu Parametern der Zeitfunktionen, vermittelt über den Fremdinterferenzabstabstand oder
-Radius (siehe oben): Um einen Kanal
herum (Ganglion) kann genau nur in ein Gebiet aliasingfrei projiziert werden, dessen Radius nicht größer ist als der durchschnittliche
Fremdinterferenzabstand (geometrische Länge der Pulspause).
Folgende Beispiele erheben keinen Anspruch auf Richtigkeit, sie sind als Hypothese zu verstehen, in welche Richtung die zu analysierende Materie erforscht werden kann. Weitere Analysen zur Codeselektion mit Laufzeitleitungen wurden in sehr verknappter Form 1993 bereits in
Kap.8b des Buches "Neuronale Interferenzen" (deutsch) beschrieben.
Beispiel 1: Sehmodell, Retina
Angenommen, die durchschnittliche Pulspause zwischen aufeinander folgenden
Pulsen beträgt bei maximaler Feuerrate T = 20 ms. die Pulsbreite soll
vernachlässigbar sein und die durchschnittliche, radiale Leitgeschwindigkeit
beträgt v = 1 mm/s (incl. synaptischer Vorgänge; willkürliche Annahmen).
Wir berechnen einen Fremdinterferenzradius von R = vT/2 = 1 mm/s · 20 ms = 10 µm.
Das heißt, daß der Abstand zweier Ganglien im Quell- oder Senkengebiet nicht
größer sein darf als R = 10 µm, um nicht Information durch Fremdinterferenzüberlauf zu verlieren.
Betrage der Ganglien-Wurzelabstand im Gebiet der Retina (~100mm²) etwa 1.000.000/100
mm² = 10.000/mm² = 100·100 pro mm², so ergibt sich ein
Fremdinterferenzradius pro Ganglion von etwas mehr als R = 10 µm, siehe Rechnung oben. Wir finden das neuronale Raster genau in dieser Größenordnung wieder. Kann das Zufall sein?
Beispiel 2: Sehmodell, visueller Cortex
Im Bereich des visuellen Cortex (VC) ist mit dem Faserbündel des
Sehnervs eine viel größere Fläche, nahezu 100 cm² = 10.000 mm²,
abzudecken. Folglich ist hier eine andere Leitgeschwindigkeit gefordert, um
Interferenzüberlauf zu verhindern. Die Faserdichte beträgt hier F =
1.000.000/10.000 mm² = 100/mm², der Fremdinterferenzradius (=
Faserabstand) ist hier etwa R = sqrt(F) = 100 µm. Nach Glg. (1) ergäbe
sich auf dieser Seite eine Leitgeschwindigkeit im Filz des VC von v = 2R/T =
2·0,1 mm/20 ms = 0,01 m/s = 10 cm/s
. Dieser Unterschied sollte sich experimentell nachweisen lassen.
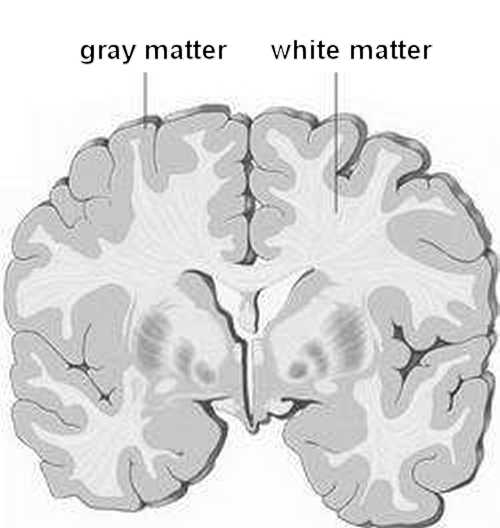 Beispiel 3: Im Cortex verkoppelte Einheiten
Beispiel 3: Im Cortex verkoppelte Einheiten
Wie aber kann bei diesem Fremdinterferenzabstand eine Verbindung in einen
anderen Teil des Cortex zustande kommen, ohne daß wir die
Fremdinterferenzbedingung verletzen? (Es sind nur 100 µm erlaubt?)
Wollen wir einen Fremdinterferenzradius von 10 cm erreichen, benötigen wir eine
Leitgeschwindigkeit von v = 2R/T = 2Rf = 2 · 100mm · 50Hz = 10.000 mm/s = 10 m/s (f: maximale Feuerrate, willkürliche Annahme hier 50 Hz). Dafür aber benötigen wir eine Myelinisierung der Nervenbahnen. Diese ist sichtbar heller als die nichtmyelinisierten Gebiete, siehe das Schnittbild des Kortex. Wieder nur purer Zufall?
Beispiel 4: Körperprojektion zum kleinen Zeh
Ist sicherzustellen, daß eine Hautoberfläche eineindeutig in irgendein
cortikales Areal kartiert, ohne daß Fremdinterferenzen zu Verwirrung führen -
das Individuum würde sensorische Erregungen nicht eindeutig zuordnen können -
ist sicherzustellen, daß der Fremdinterferenzradius R groß genug im
Verhältnis zur zu kartierenden Oberfläche ist. So würden wir für einen
Fremdinterferenzabstand R = 2 m (Abstand Cortex - Zeh) bei einer
willkürlich angenommenen Feuerpause 1/f entsprechend f = 30 Hz eine
Leitgeschwindigkeit von v = 2Rf = 2 · 2m · 30Hz = 120 m/s benötigen. Denken
wir jetzt an die Leitgeschwindigkeit peripherer, myelinisierter Nerven? Diese
liegt in der Tat bei etwa 120 m/s . Natürlich sind dies nur grobe
Anhaltspunkte. Im Detail wissen wir, daß unterschiedlichste
Fasergeschwindigkeiten anzutreffen sind, das Nervensystem ist schwerwiegend
inhomogen verschaltet.
Was bedeutet aber diese zufällige Übereinstimmung? Sie kann nur bedeuten, daß die Natur eine Lösung für die unlösbare Klingeldrahtfrage fand: Um Leitbahnen einzusparen, ist offenbar nicht nur der Cortex, sondern auch das sog. periphere Nervensystem (teilweise) interferenziell verschaltet.
Beispiel 5: Multiple Sklerose
Erst aus Sicht der Interferenznetze ist das Krankheitsbild der multiplen Sklerose analysierbar (vgl. NI93). Bei dieser Erkrankung sinkt u.a. die
Leitgeschwindigkeit myelinisierter (i.a. peripherer) Nerven.
Da die geometrische Wellenlänge gleich Leitgeschwindigkeit mal Pulspause ist, verringert sich diese.
Fremdinterferenzkarten wandern damit in den Bereich der Selbstinterferenzkarten ein, siehe Schmerzmodell. Das heißt, daß periphere Aktorik (Muskeln) wie auch periphere Sensorik (Tastsinn etc.) nicht mehr eindeutig adressiert/gesteuert/zugeordnet werden können, siehe Beispiel 4.
Fremdinterferenzen schleichen sich in Gebiete, die eigentlich durch Selbstinterferenz eindeutig adressiert werden müssten.
Aus der Theorie der IN können nun die fatalen
Folgen vorhergesagt werden, die wieder zufällig genau mit den medizinischen Befunden übereinstimmen: Sensorisch sind Mehrdeutigkeiten in der
Interpretation von Ortszuordnungen zu erwarten, motorisch können wir davon
ausgehen, daß jede gewollte Muskelerregung selbstinterferentieller Art dutzende
ungewollter Bewegungen fremdinterferentieller Art (an ungewollten Stellen) mit
sich bringt. Verkrampfungen und Zuckungen wären die
Folge (Spastik, Tremor, Schmerz). Eine Simulation des Vorgangs hat große Nähe zum Schmerzmodell.
Zur Abhilfe könnten Pharmaka dienen, die die Leitgeschwindigkeit v
erhöhen oder/und die die Pulspause T (als sog. Refraktärzeit) verlängern, siehe Gleichung (1).
Beispiel 6: Kurzzeitgedächtnis
Wir erinnern uns, daß unterschiedliche Fremdinterferenzradien an
unterschiedliche Leitgeschwindigkeiten gekoppelt sind. Und unterschiedliche
Leitgeschwindigkeiten sind an unterschiedliche Zelltypen, Synapsen und Layer gebunden.
Fragen wir uns, wie ein Kurzzeitgedächtnis (Platon: pantha rhei - alles
fließt) zustande kommt, und was dies sein könnte - schließlich wollen wir auch
noch zwei Minuten nach Ankunft des Kollegen ahnen, daß er noch hinter uns steht,
ohne uns schon wieder nach ihm umdrehen zu müssen - so haben wir ein Problem.
Einerseits ist zu vermuten, daß sich die völlig unterschiedlichen
Informationen, die hier i.a. zu verknüpfen sind, nicht in nächster Distanz
zueinander im Cortex befinden. Größere Distanzen aber bedeuten höhere
Leitgeschwindigkeiten, nehmen wir v = 2Rf = 20 m/s, soll die Selbstinterferenzkarte erhalten bleiben.
Um aber einen Impuls zwei Minuten lang durch den Cortex laufen lassen zu können, benötigen wir das
Gegenteil: wir benötigen sehr kleine Leitgeschwindigkeiten, vielleicht v =
s/t = 20 cm/100s = 2 mm/s. Das wäre ein Faktor von Zehntausend weniger.
Eine Lösung des Problems bestünde darin, die Information zunächst schnell
dorthin zu bringen, wo sie verknüpft wird und dort in ein anderes
Interferenznetz einzukoppeln, welches 10.000 mal langsamer ist. Dieses hätte
dann aber auch nur einen Fremdinterferenzabstand von R = vT/2 = 2mm/s · 20ms/2 =
20 µm.
Was bedeutet das? Es bedeutet nicht mehr und
nicht weniger, als daß das grobe Netz (10 m/s) im feinen Netz (2 mm/s) keinen
Ort mehr separieren kann. Der Ort verschwindet bei dieser Operation, was bleibt
ist die Zeit, ist nur der Zeitbezug! Unser Kurzzeitgedächtnis läßt sich dann nur als ein entartetes, zu schroff gekoppeltes Interferenznetz interpretieren, aus dem die Physik die Ortszuordnung verschwinden läßt.
Beispiel 7: Hörkarten
Wollen wir nicht Ortszuordnungen, sondern frequenzsensitive 'Hörbilder' oder codeabhängiges Verhalten als Integral-Karte (Interferenz-Integral: I²) aufbauen, benötigen wir genau das Gegenteil: wir benötigen dazu die Fremdinterferenzen (außerhalb des Selbstinterferenzradius), siehe oben.
Wir gehen davon aus, daß bei der Erkennung eines Tones das Selbstinterferenzintegral auf Neuronen-Format schrumpft, so daß es keinen bildlichen Inhalt mehr benötigt. Sodann interessieren wir uns ausschließlich für die Fremdinterferenzkarte. Es wäre, als würden wir aus Abb.6-1, g) mit v = 100 noch viel weiter herauszoomen, z.B. mit v = 1000. Dann schmelzen die "G" je zu einem Punkt zusammen und wir erblicken die Fremdinterferenzkarte z.B. eines Geräusches.
Um zu prüfen, ob die Proportionen auch mit der nervlichen Realität übereinstimmen, machen wir folgende Rechnung. Nehmen wir (willkürlich) aus dem auditiven Cortex eine Leitgeschwindigkeit v = 10 mm/s und eine zu kartierende Frequenz f = 1 kHz, so erhalten wir einen Fremdinterferenzradius
R = v/(2f) = 10 mm/s /(2 · 1000 Hz)
R = 5 µm
In der Tat ist dieser Fremdinterferenzabstand wirklich geeignet, die Selbstinterferenzabbildung auf Neuronengröße zu reduzieren! Damit kartieren bei dieser Konstellation nur noch Frequenzen, Klänge oder Geräusche. Sie ergeben ein Bild - aber nur des Geräuschs. (Haben wir das Potential dieser einfachen Rechnung schon erfasst?)
Kleines Fazit
Hätten Sie gedacht, daß elementare Eigenschaften eines Nervensystems so einfach zu berechnen sein würden? Ich war bei jeder Beispielrechnung aufs Neue überrascht von der Paßfähigkeit der Proportionen.
Stellen wir uns zum Schluß noch die Frage, warum Primaten im Frequenzbereich zwischen 100 Hz und 10 kHz hören, so kommt plötzlich ein neuer Aspekt ins Spiel: die Geometrie des Nervensystems muß zum Frequenzbereich passen, damit die Fremdinterferenzkarten hineinpassen. Dies impliziert auch, daß Tiere in anderen Frequenzbereichen hören können, man denke zum Beispiel an Delfine oder Fledermäuse.
Haben wir schon darüber nachgedacht, warum wir einen vorbeirasenden
Wagen nicht in Einzelbildern wie im Film sehen können? Was ist anders an unserem
Nervensystem im Verhältnis zur technischen Welt um uns herum? Warum ist unser
Denken nicht auf die zwei Dimensionen des Filmbilds beschränkt? Warum und wie
nehmen wir die uns umgebende, n-dimensionale Welt war?
Da wir bereits erkannt haben, daß der Zielort einer Information in Interferenznetzen nicht durch Verdrahtung, sondern durch Verzögerungen entsteht, wollen wir uns den Einfluß eines Delays auf das Interferenzintegral ansehen. Wir wählen einen ähnlichen Versuchsaufbau wie beim Zooming. Als Generator dienen G-förmig angeordnete, pulsende Pixel. Über die Kanäle wird wieder mit vorwärtslaufender Zeit in Empfangsfelder hineinprojiziert.
Wir berechnen dazu Bilder für Verzögerungen (Delays) eines einzelnen Kanals von dt = +4 bis -12 ms.

Abb.10-1: Interferenzielle Projektion zwischen zwei neuronalen Feldern, die über drei Axonen verbunden sind mit Veränderung einer Dreikanalprojektion bei variierendem Delay eines Kanals. Bild modifiziert nach GFaI-Jahresbericht 1994 Bild 6, S.69
(PDF). Erste Veröffentlichung in
(Bionet96), Fig.8.
Zur Simulation wird in die Leitbahn eines Kanals eine variable Verzögerungszeit dt geschaltet. Wir sehen, daß sich das Bild im Empfangsraum bei Variation der Verzögerungszeit eines Kanals zu verschieben beginnt. Der Bildmittelpunkt verschiebt sich zur Seite des höheren Delays.
Die Bedeutung dieser Simulation läßt sich kaum ermessen. Es genügt die Veränderung von Leitgeschwindigkeiten oder Delays
(dt), damit Bilder im Cortex anfangen zu wandern oder sich zu bewegen. Die Änderungen können wir übrigens indirekt mit dem EEG messen: Potentialänderungen (EEG) in der Glia bewirken Leitgeschwindigkeitsänderungen in Dendriten und Axonen.
So messen wir im EEG wahrscheinlich nur Steuerpotentiale für Zooming und Movement. Anders gesagt: Wir messen im EEG nicht Informationsinhalte, sondern Steuerparameter, die den Weg von Informationen festlegen! Aus Sicht der Informatik analysieren wir im EEG also nicht Daten, sondern Adressen.
Wozu braucht es einen Homunculus?
Wenn wir rekapitulieren, daß Zielgebiete einer Information in Interferenznetzen
nicht über Leitbahnen, sondern über Delays vorgegeben werden, und wir uns an
Penfields Homunculus erinnern, bei dem viele Zielgebiete nebeneinander zu
rangieren sind, beginnen wir die gewaltige Leistung zu erahnen, die über
Zooming und Movement zu erbringen ist. Nur wenn dank Zooming und Movement jede
Partialkarte exakt in ihr Zielgebiet projiziert wird, arbeitet das Gesamtsystem
ohne Verwirrung!
Wenn wir uns daran erinnern, daß im
Daumenexperiment
bereits 1992 gefunden wurde, daß sich Wellenfronten nach der Ausrichtung des
Daumens orientieren, so ahnen wir außerdem, wofür eigentlich der sensorische
und motorische Homunculus benötigt wird, und warum beide in einem genau
definierten Streifen des Cortex liegen. Prinzipiell könnten wir davon ausgehen,
daß der Homunculus überflüssig wäre. Wozu aber
wird diese merkwürdige Schnittstelle der motorischen und sensorischen
Körperprojektionen benötigt?
Nehmen wir an, eine Dehnung oder Biegung der Wirbelsäule läßt - wie beim Daumen -
die aufsteigenden Projektionsfelder seitlich ausweichen. Dann kämen alle aufsteigenden, sensorischen
Informationen im Cortex an falschen Orten an! Umgekehrt kämen alle
absteigenden, motorischen Informationen ebenfalls falsch an. Statt des kleinen Zehs würde
sich der Oberschenkel bewegen. Um dies zu verhindern, bedarf es spezieller
Schnittstellen, die mit Steuerinformationen aus dem Wellenfeld dessen
Feldausrichtung korrigieren. Im Cortex dient dazu offenbar der
Homunculus.
An diesen wird sowohl aus dem Cortex, als auch aus dem Rückenmark eine
sozusagen mit Zooming und Movement normierte Abbildung zur Weiterverarbeitung
gereicht.
Der Informationsaustritt aus dem Rückenmark übrigens wird über eine genial
einfache, hyperbolische Projektion
gerichtet.
Obiges Bild zeigt weiter, daß einfache, digitale Schwellwertschaltungen
nur durch Veränderung eines einzigen Leitbahn-Delays in der Lage wären, Bilder (2D/3D) im Raum wandern zu lassen. Für Nervennetze ergibt diese Schaltung eine prinzipielle Möglichkeit, einen Gegenstand ein Stück weit parametrisch zu verfolgen oder dessen Formänderung adaptiv anzupassen. (Im Computer werden Bildbewegungen - wie auf der Leinwand - durch völlig andere Verfahren gelöst, die nicht auf die Natur übertragbar sind.)
(Abstraktion für Kolumnen des visuellen Cortex)
Interferezielle Projektion bildet eine Art einer geometrischen Codierung, wenn viele Kanäle dicht im Quellgebiet angeordnet werden. So konvergieren auf der Retina (Auge) rund 130 Millionen Rezeptoren auf eine Million Ganglienzellen, d.h. ein 'Kanal' (Ganglion) versorgt 130 Rezeptoren. Ein entsprechendes, grob vereinfachtes Interferenzmodell zeigt wesentliche, interferenzielle Eigenschaften solcher Strukturen. Siehe dazu folgende 16-Kanal Projektion eines GH (unten) auf ein gegenüberliegendes Gebiet (oben).

Abb.11-1: 16-Kanal Projektion. Informationreduktion zwischen zwei korrespondierenden Feldern. Dies ist offenbar auch eine Art von Hologramm. Nur hier im Web veröffentlicht.
Wird eine Vorlage an geeigneten Stellen abgelauscht, lassen sich Interferenzintegrale entwickeln, die von nur sehr wenigen Neuronen synthetisiert werden können. Hintergrund ist die Möglichkeit, daß in einer beliebigen Raumdimension (Inhomogenität) jede Abbildung dekomponierbar und reduzibel ist auf ein Neuron, Herleitungsansätze siehe [NI93]. Als eine mögliche, biologische Entsprechung entdecken wir Rizzolatti's
Spiegelneuronen.
Während unser Originalbild (GH unten) aus etwa 40 feuernden Neuronen bestehen möge, sehen wir oben nur drei stark aktivierte Bereiche (Peaks). Diese repräsentieren das untere Bild. Würden wir zusätzliche, inhomogene Fasern einbeziehen, ließe sich ein einzelner Interferenzort finden, der das gesamte GH repräsentiert. Mit anderen Worten: hier findet eine Abstraktion und Informationsreduktion statt. Das komplexe GH unten konvergiert im Feuer von drei Neuronen oben. Die Karten unten und oben interferieren miteinander, die eine ist das Gegenstück der anderen, mehr siehe [NI 1993]
'Permutation' Kap.5, S.100 ff.

Abb.11-2: Äquivalenz einer höherdimensionalen Abbildung links mit drei niederdimensionalen rechts. Nach diesem Prinzip kann ein einzelnes Neuron eine beliebig komplexe Abbildung oder Zustandsfolge referenzieren (finden wir z.B. im Homunculus). Weil eine hochkanalige Projektion stets auch niederkanalige (holografische) Teile besitzt, konnten sich Karl Lashleys Ratten wohl erinnern. Quellen [NI93], Kap.5, S.100, interferentielle Codierung durch Permutation. Published in [SAMS94], p.157, Fig.11
Zum Prinzip der Permutationen nach [NI93]: Wenn alle Laufzeiten zwischen
Quelle und Senke zwischen Teilräumen P12, P23, P34 und P1234 identisch sind, ist eine Umcodierung möglich. Hier werden drei Interferenzorte P12,
P23, P34 niederer Raumdimension durch einen Ort P1234 höherer Dimension gebunden. Wir erkennen eine neue Problematik: Während die Verschaltung von links nach rechts funktioniert, geht es von rechts nach links nicht ganz so gut (siehe Überbestimmtheitsproblem). Wir benötigen entweder eine Synchronisation (hierbei kaum denkbar); wir müssen separat gleichbestimmt einkoppeln (k = d+1) oder wir müssen zeitlich verzögern/integrieren. Die vielfältige Bedeutung dieses Bildes für die Neurowissenschaften läßt sich im Moment nur erahnen.
Interpretation
Wählen wir eine lokale Nachbarschaft aller Neuronen des Empfangsfeldes, so könnten wir Parameter so wählen, daß je eine Nachbarschaft um ein hier aufsteigendes Axon herum gespiegelt nach oben gebracht wird. Die obere Karte sähe dann aus, wie durch eine mit Blasen strukturierte Glasscheibe betrachtet: in jeder Blase spiegelt sich das untere Detail, insgesamt aber wird die Karte ungespiegelt wiedergegeben. Eine Kolumnen-Organisation wird sichtbar.
Es deutet vieles darauf hin, daß dies die Lesart des visuellen Cortex ist.
Eine andere Lesart entsteht bei globaler Kopplung, wie im Bild dargestellt.
Hier entstehen völlig andere Bildqualitäten, die auf Mechanismen der
Abstraktion hindeuten.
Einerseits verdeutlicht das Bild die zwangsläufige Ausbildung von 'Kolumnen' um Ganglien herum, andererseits lassen sich mit dem 1:130-Verhältnis alle Parameter bestimmen, die zur Berechnung des Interferenzsystems Retina - Ganglion - visueller Cortex beitragen.
Da wir wissen, daß ein einzelnes Neuron nicht unterscheiden kann, ob es Informationen der Augen, der Ohren, der Nase, des Sprechorgans oder der Bewegungsorgane verarbeitet - es sind immer nur Pulse, die es 'sieht' - so können wir adäquate Modelle für Sprechen/Hören oder Bewegung beobachten/ausführen aufstellen. In allen Fällen bildet ein komplexeres Interferenzintegral auf ein abstrakteres durch interferenzielle Permutation (mehr siehe Manuskript Neuronale Interferenzen, gh 1993) ab. Dabei ist es gleichgültig, ob der Ursprung der Karten aus Fremdinterferenzen (Hörkarten, spektrale Karten, Verhaltenskarten) oder aus Selbstinterferenzen (Bildern) stammt. Wesentlich für die Berechnung sind nur die Raum-Zeit-Parameter zwischen Quellfeld, Kanälen und Senkenfeld.
Wie ist es möglich, daß Millionen Sensoren unserer Beine ohne
Verschaltungsfehler spiegelverkehrt auf den sensorischen Teil des Homunculus
projizieren, ohne daß der eine oder andere Schaltungsfehler uns vorgaukelt, der
linke große Zeh wäre rechts und umgekehrt? Steht der Natur ein Code zur
Verfügung, Bilder der Gedanken ineinander zu verweben oder Ideen miteinander zu
kombinieren?
Um dies zu prüfen, addieren wir einfach die Zeitfunktionen von je drei Kanälen
zweier Generatorfelder. Wir hängen zwei zuvor generierte Kanaldatensätze, eines 'g' und eines 'h' zusammen (to append).

Abb.12-1: Projektion zweier Generatorräume (oben) auf einen Detektorraum (unten). Schwarz markierte Orte pulsen. Die Zeitfunktionen der Generatorräume wurden vor der Rekonstruktion aneinandergehängt.
Im Detektorraum überlagern sich die Bilder auf höchst bemerkenswerte Weise. Es ist nicht mehr nachvollziehbar, aus welchem Quellbild die jeweilige Erregung im Detektorraum stammt. Hier verschmelzen zum ersten mal zwei Bilder zu einem. Wie schon C.S. Peirce (1837-1914) 1902 bemerkte:
"All thought is in signs".
Die Grundlage der Semiotik bildet der Zusammenhang zwischen dem in jeder Sprache anders gesprochenem Wort, wie "Sonne", dem in jeder Sprache anders geschriebenen Wort und der überall gleichen, damit verbundenen Vorstellung.
Was bedeutet Semiotik bezogen auf unsere Interferenzintegrale? Das gehörte Wort bildet eine Geräuschkarte, siehe oben. Diese assoziiert mit einer bildlichen Karte, genannt Vorstellung vom Gegenstand. Beide können dann noch über Permutation mit einer Schriftkarte assoziieren - allerdings wird es hier komplizierter.
Prinzipiell können Zeitfunktionen-Bündel technisch aneinander angehangen (to
append) oder aufeinander aufaddiert werden (to add). Von Nervenzellen können sie nur addiert werden. Der Unterschied zwischen beiden Methoden besteht in einem geringer werdenden, sich etwa halbierenden Pulsabstand bei Addition gegenüber dem Anhängen, mit der Konsequenz eines Heranrückens der Fremdinterferenzen.
Je mehr Additionen von Zeitfunktionen pro Kanal erfolgen (mehrerer Sinneseindrücke gleichzeitig), umso dichter werden die Pulsfolgen, umso näher rücken die Fremdinterferenz-Abstände ins Bild. Wir alle kennen dieses Phänomen. Bei einem Unfall überschlagen sich unsere Gedanken und wir können keinen klaren Gedanken mehr fassen, weil die Fremdinterferernzen ins Bildfeld rücken und uns verwirren.
Bis 1996 beschäftigte mich die Frage, was eigentlich passiert, wenn wir Quellorte der Kanäle in einem Detektorfeld beliebig herumschieben. Da Sie sich, wohl genau wie ich damals, solche Interferenzintegrale
nicht vorstellen können, müssen wir sie simulieren. Wir benutzen dazu wieder
den Kanaldatensatz der konjugierten Abbildung aus Abb.12-1 und verändern die Quellorte im Detektorraum.
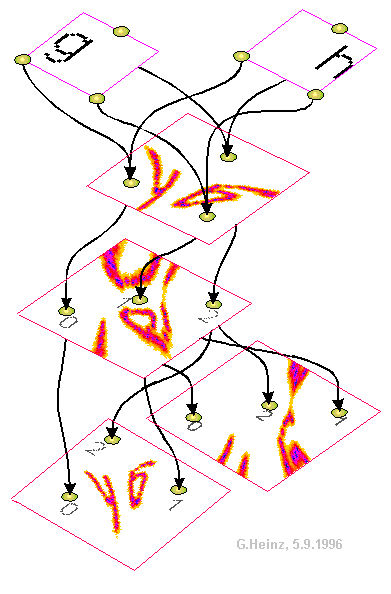
Abb.13-1: Topologische Projektionen in verschiedene Detektorräume. Variation der
Kanalanordnung bewirkt partielle Zooming- und Moving-Effekte, partiale
Bildbegrenzung, Bildverzerrung oder multiple Erscheinung. Der topologische
Zusammenhalt der Projektionen läßt sich nicht auflösen. Die Bilder g und h verschmelzen.
Die entstehenden Interferenzintegrale sehen aus, als ob sie von einem Gumminetz
zusammengehalten werden. Es ist zu erkennen, daß Nachbarschaften nicht
zerreissen. Die lokale Nachbarschaft bleibt stets erhalten, sie kann nicht
getrennt werden.
Beim Movement
lernten wir, daß im Unterschied zur Hausklingelanlage in Interferenznetzen
nicht der Draht die Richtung des Informationsflußes anzeigt. Es sind
Verzögerungszeiten und es ist die Gleichzeitigkeit des Eintreffens mehrerer
Impulse, die den Zielort definieren.
In Interferenznetzen entstehen nur an interferentiell definierten
Orten Erregungen. Folglich gibt die Laufzeit-, die Quell- und Senken-, sowie
die (zeitliche) Kanalgeometrie der Übertragungsleitungen die Abbildung einer
Generatorkarte auf eine Detektorkarte wieder. In die Übertragungsleitungen
können beliebig viele Abzweigungen eingeschaltet sein. Die Adresse der Daten
richtet sich bei interferenzieller Übertragung nur nach dem Interferenzort, nie nach der Geometrie oder Ausfächerung der Leitbahnen (Nervenverästelungen).
Man beachte das entstehende Problem an einem Faserbündel, welches Abbildungen transportiert. Parametrische Schwankungen der Leitgeschwindigkeit können im Bündel ein Movement der Maxima bewirken, welches dazu führt, daß die gewünschte Abbildung außerhalb der
Faser-Achse entstehen kann. Verläßt die Abbildung den neuronalen Raum oder das Interferenzfeld aber körperlich, so kommt sie nicht zustande!
Es steht zu befürchten, daß diese Problematik bei vielen Nervenerkrankungen als Ursache zu finden sein wird. Lange bevor ein Nerv stirbt, verändern sich dessen Parameter: Und damit unsere Bilder (Integrale) verrutschen, genügt eine winzige Änderung der Leitgeschwindigkeit.
Wenn Bilder aber verrutschen, rutschen sie aus dem Netzwerk ins Nichts oder im Netzwerk in eine benachbarte (Partial-) Karte: den ersten Fall können wir in Analogie bezeichnen als Vergessen, den zweiten als Verwirrung.
So gibt es vielleicht doch noch Hoffnung für Alzheimer und Parkinson? Sind
beide Krankheiten etwa von initial gleicher Ursache? Sind große Gebiete von
Nervenbahnen betroffen, so ist zu erwarten, daß Abbildungen durch
Veränderung der Laufzeitstruktur zunächst unschärfer oder verzerrt werden.
Was heißt übrigens aus dem Netzwerk ins Nichts? Denken wir bitte daran, daß
jeder n-kanalige Interferenzort durch eine (mindestens) n-stellige Maske mit n Delays definiert ist. Bricht aufgrund eines synaptischen Ausfalls ein Kanal weg, so wäre die Information nicht mehr abrufbar (vergessen). Deshalb müssen immer viel mehr Kanäle beteiligt sein. Aber Vorsicht: Ausfallsicherheit wird im Interferenznetz durch Überbestimmtheit (Kanalzahl n > Dimension d+1) erkauft! Und Überbestimmtheit begrenzt die Möglichkeiten für Zooming und Movement.
5.4 Zur Rolle der Überbestimmtheit
Sind Sie Wissenschaftler, Musiker oder Boxer? Wird aus Verletzungsgründen Redundanz gefordert, so werden hochkanalige Abbildungen von Vorteil sein. Diese aber unterdrücken zarte, schwache Emissionsquellen. Als Wissenschaftler haben Sie es sicher auch schon bemerkt: Die besten Einfälle kommen nachts um halb drei, wenn man nicht wieder einschlafen kann. Die Dunkelheit sorgt für relative Stille im Cortex. Auch schwache Assoziationen werden jetzt lebendig, wir haben grandiose Ideen, die sich aber meist am folgenden Tag als nicht ganz so brillant herausstellen.
Ganz anders bei einem Boxer. Was bedeutet dies zum Beispiel für einen Boxer, dessen Nervennetz permanent durch harte Schläge geschädigt wird? Er muß stark überbestimmte Abbildungen antrainieren. (Wie er das macht, wissen wir nicht). Wenn wir aber daran denken, daß hohe Überbestimmtheit die Fremdinterferenzen blockiert und Flexibilität bei Zooming und Movement kostet, so ist der Boxer in einer aussichtslosen Situation:
Entweder sein Nervennetz wird durch viele Verletzungen unflexibel (überbestimmt): Dann wird er zum "Nehmer-Typ". Oder er teilt Schläge aus, kassiert wenig, und bleibt geistig flexibel (intelligent). Denken wir an die Biographien großer Boxer (Cassius Clay alias Muhammad Ali), so ahnen wir, daß da "was dran sein könnte".
5.5 Nervliche Erkrankungen
Würden wir im Bild oben eine Leitgeschwindigkeit eines einzigen, übertragenden Kanals ändern, würde die Projektion sofort ausscheren.
Um effizient bildliche Projektionen übertragen zu können (man denke an das Faserbündel Retina - Sehbahn - visueller Cortex) muß eine Million Fasern exakt abgeglichene Laufzeiten bzw. Leitgeschwindigkeiten aufweisen. Falls nicht, wandert eine Karte in eine benachbarte Karte hinein und es gibt Verwirrung, siehe oben. Für Neurobiologen eine interessante Aufgabe, zu untersuchen, welche Mechanismen für diesen Abgleich eigentlich sorgen.
Ein Beispiel, was passiert, wenn sich Leitgeschwindigkeiten ändern, bietet die multiple Sklerose. Hier sterben vielleicht auch Synapsen oder Nervenfasern ab. Aber es verändert sich infolge einer langsamen Myelin-Auflösung (Isolation der Fasern) meßbar die Leitgeschwindigkeit, sie sinkt ab, nicht mehr myelinisierte Fasern werden etwa um eine Zehnerpotenz langsamer. Erfolgt dieser Prozess nicht gleichmäßig in einem Faserbündel, wandern oder zoomen Interferenzorte hinaus, oder die Abbildungen verlöschen. Man nennt dies Lähmung.
Ganz abgesehen davon, daß der Fremdinterferenzradius dann bei gleichbleibender Feuerrate kleiner wird - das System kann dann Orte nicht mehr eindeutig identifizieren oder steuern. Abhilfe würden Medikamente bieten, die die Feuerrate verringern. Das sind übrigens aus Sicht der Interferenznetze Schmerzmittel - siehe dazu eine Schmerzsimulation.
Aha, werden Sie jetzt vielleicht sagen: Offenbar werden auch Muskeln über
Interferenzen und nicht über Klingeldrähte gesteuert! Wäre auch nicht
verwunderlich, schließlich leben Nervenzellen nur sieben Jahre. Und nur
Interferenznetze sind ausfallgesichert. Sie kennen sicher die Konsequenzen,
wenn der Klingeldraht im Haus ausfällt: Dann kann der Postbote den Klingelknopf drücken, aber die Klingel bleibt still. Das sollte im Nervensystem nicht passieren.
Es ist auch möglich, den Interferenzort durch Hinzunahme weiterer Leitbahnen
einzuengen - wir kommen dann zu den Fragestellungen der überbestimmten
Pulsprojektionen, die nur durch gefaltete n-Dimensionalität gebrochen werden
können (mehr siehe NI93).
14.1 Raum-zeitliche Muster
Nun wollen wir untersuchen, wie Fremdinterferenzen (Codes oder Frequenzen) kartieren.
Vielleicht erinnern wir uns an den Huygenschen Doppelspaltversuch. Dieser liefert Interferenzlinien, deren Abstand voneinander die entsprechende Frequenz codiert.
Mit Bio-Interface/PSI-Tools kann man dies simulieren. Um es einfach zu machen, werden wir testen, wie Interferenzmuster eines Kanals aussehen, der mit sich selbst (mehrfach) interferiert.
Im Maximum (Selbstinterferenz) interferieren Wellen i mit sich selbst
(dargestellt als i·i). Sie interferieren aber auch mit dem Vorgänger und dem
Nachfolger (Fremdinterferenz), dargestellt als i·(i-1) oder i·(i+1) etc.. Bei
Phased Array Antennen oder Mikrofonen heißen die Fremdinterferenzorte
'Nebenkeulen'. Zwischen beiden besteht ein Wesensunterschied: während
Abbildungen die Selbstinterferenz betonen, benötigen z.B. Frequenzkarten im
Nervensystem ausschließlich die Fremdinterferenzen.
(Hinweis: Hier dargestellte Simulationsergebnisse sind auschließlich unter
Verwendung von Zeitfunktionen entstanden -> Non-materialistic field theory)


Abb.14-1: Zwei Varianten des Huygenschen Doppelspalt-Experiments mit verzögernden Leitbahnen. Bildquelle
[NI93], Kap.2a, S.54
Für den Fall, daß die geometrische Größe des Interferenzfeldes größer ist, als
die Wellenlänge (Geschwindigkeit mal Pulsfrequenz), werden Fremdinterferenzen
zwischen Impulsen von ursprünglich verschiedenem Zeitbezug sichtbar. Es wird
deutlich, daß dies die Art sein könnte, in der die Biologie Frequenzen,
frequenzcodierte Sensoramplituden oder serielle Codes vermittels deren
Ortszuordnungen speichern oder auswerten kann.
Für den zweikanaligen Fall erhalten wir das bekannte, Huygensche Doppelspaltmuster, hier allerdings an das
Vorhandensein von Leitbahnen gebunden. Der Ausgang eines virtuellen, an die
Quellknoten angeschlossenen AND-Gatters würde nur in Orten hoher
Interferenzwerte pulsen, an Orten niederer Interferenz bliebe er still.

Abb.14-2: Interferenzkarten einer periodischen Pulsfolge, die verzweigt von mehreren Quellorten in ein (homogenes) Detektorfeld geleitet wird. Simulationen mit Bio-Interface/PSI-Tools 1996, publiziert in
[NF2002] Fig.7, p.5
Bei geeigneter Dimensionierung treten Pulse mit Vorgängern und Nachfolgern in Interferenz, es entsteht ein Interferenzmuster mit Maximum und Nebenkeulen. Das Maximum charakterisiert die Selbstinterferenz (Interferenz von Welle i mit i, die Nebenmaxima charakterisieren Fremdinterferenzen). Je nach Kanalzahl und -Anordnung entstehen andere Bilder.
Bliebe noch anzumerken, daß sich der Wert des Ortes der Selbstinterferenz umso stärker von Orten der Fremdinterferenz abhebt, je höher die Kanalzahl ist.
Mag man Frequenzen detektieren, könnte man sich zwei Leitbahnen unterschiedlicher Geschwindigkeiten va und vb vorstellen.

Abb.14-3: Frequenzdetektion mit zwei Leitbahnen unterschiedlicher Leitgeschwindigkeit va und vb. Neuronen N mögen vom AND-Typ sein (multiplikativ). Bildquelle
[NI93], Kap.8b, S.184
Je nach benutztem Abgriff werden verschiedene Frequenzen detektiert. Für Details, siehe [NI93], Kap.8b.
14.2 Harmonien, Musik, Töne, Sequenzen, Codes, Verhalten
Wie können in Interferenznetzen Töne oder zeitliche Verhaltensmuster
erkannt werden? Natürlich auch nur als Interferenzintegrale. Da die Nervenzelle nicht sieht, woher eine Zeitfunktion kommt, ob von der Nase, vom Bein, vom Auge oder vom Ohr, macht sie immer dasselbe: sie integriert Erregung auf.
Dr. Friedrich Blutner machte auf eine interessante Geschichte aufmerksam. "Pythagoras in der Schmiede" ist eine antike Legende, die beschreibt, wie Pythagoras in einer Schmiede entdeckt haben soll, dass gleichzeitige Hammerschläge dissonante oder wohlklingende Töne erzeugen können, siehe diesen
Link auf Wikipedia.
Ohne auf Details dieser Legende einzugehen, entstand daraus eine erste, musiktheoretische Abstraktion. Pythagoras soll in Verhältnissen zwischen bestimmten ganzen Zahlen (16, 12, 9, 8, 6, 4) Harmonien entdeckt und damit die Musiktheorie begründet haben. Seine Zahlen sollen das Gewicht von Hämmern markiert haben, dem Wert "16" käme dabei die tiefste Frequenz zu.

Abb.14-4: Franchinus Gaffurius: Theorica musivae (1492). Pythagoras exploring harmony and ratio with various musical instruments. Source: en.wikipedia.org (Link)
Franchinus Gaffurius faßte 1492 diese Pythagoräische Musiktheorie in einem Bild zusammen.
Ganz abgesehen davon, daß die Legende physikalisch unklar ist, hat sich in Gaffurius Bild auch noch ein Fehler eingeschlichen. Während bei den Hämmern, Glocken und Flöten der Wert "16" zum tiefsten Ton gehört, markiert er beim Saiteninstrument und bei den Gläsern den höchstfrequenten Ton.
Hier wollen wir die Pytagoräischen Werte als frequenzproportional betrachten.
Im Kern geht es beim Wohlklang um Interferenzen. Haben Frequenzen bestimmte, ganzzahlige Teiler, z.B. 12:6 = 2:1 (Oktave) oder 12:8 = 3:2 oder 9:6 = 3:2 (Quinte) oder 12:9 = 4:3 oder 8:6 = 4:3 (Quarte) so sprechen wir von Harmonien. Bei anderen Verhältnisse empfinden wir Überlagerungen als dissonant.
Wir setzen voraus, daß die am Ohr eintreffenden, akustischen Schwingungen bereits vorab in dichte-modulierte Pulse konstanter Amplitude gewandelt wurden.
Im Kapitel 5 des Buchs "Neuronale Interferenzen" Seiten 116 ff.
(Link)
sind die Grundlagen skizziert, leider schwer lesbar.

Abb.14-5: Erregung eines Neurons durch Fremdinterferenz (Autokorrelation). Kommen in einem Pulsmuster korrelierte Pulse im zeitlichen Abstand δ vor, wird das Neuron eher erregt. kτ möge eine konstante Verzögerungszeit sein, die auf beiden Pfaden auftritt. Quelle
[NI93], Kap.5, S.117
(Die Verzögerungen kτ können beliebige Werte ≥ 0 annehmen, hier z.B. Null.)
Gehen wir von auf Eins normierten Impulsen aus, so wirkt die Schaltung (vereinfacht, ohne Refraktärzeit) wie ein Kammfilter mit der Ausgabe y(t)
Beide Eingabewerte müssen Eins sein, damit die Ausgabe Eins wird, die Schaltung hat multiplikativen oder AND-Charakter.
Die Maxima liegen auf ganzzahligen Vielfachen n der Frequenz
f = 1/δ, d.h. auf
Beispiel: Für δ = 2,27 ms würde die Schaltung auf Frequenzen f mit einer Schwingungsdauer von 440, 880, 1320, 1760 Hz reagieren.
Unter der Annahme, die Maxima akustischer Schwingungen sind als dichtere Pulsmuster codiert, detektiert ein geeignetes Interferenznetzwerk Harmonien automatisch, wenn die Verzögerungswerte entsprechend eingestellt sind:

Abb.14-6: Interferenzen von Pulsfolgen bei Oktave, Quinte und Quarte (Prinzip). Rechts steht der Teiler. Ein Puls steht für ein Maximum einer akustischen Schwingung.
Die Idee dahinter ist folgende. Jeder hereinkommende Impuls durchläuft alle Verzögerungsleitungen
τ1, τ2, τ3, τn.
Treffen am Soma zwei harmonisch verzögerte Pulse zusammen, erkennt das Neuron den "hit".
Bei Schwellwerten von 0,5 wird die Wahrscheinlichkeit des Feuerns bei zeitlicher Korrelation zweier Synapsen hoch sein ("hit"). Damit werden Harmonien betont, Dissonanzen werden unterdrückt.
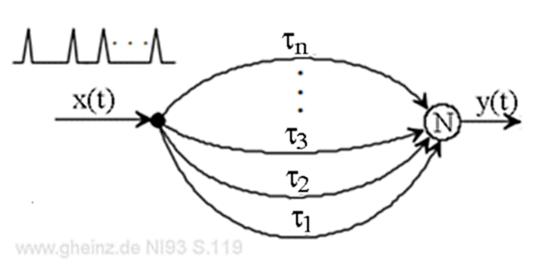
Abb.14-7: Einzelnes Neuron N als Interferenzkreis, der auf Harmonien ansprechen kann. Verzögerungen τ kann man Tab.1 entnehmen. Bildquelle [NI93], Kap.5, S.119 (modifiziert)
Tab.1: Verzögerungen τi, τj, τk, τn für Oktave, Quinte und Quarte bezogen auf den Kammerton a1 = 440 Hz
| Teiler |
6 |
8 |
9 |
12 |
| Harmonie |
f0 |
4/3 f0 |
3/2 f0 |
2 f0 |
| Frequenz f |
440 Hz |
587 Hz |
660 Hz |
880 Hz |
| Delay τ = 1/f |
2273 µs |
1705 µs |
1515 µs |
1136 µs |
Den einzelnen Pfaden können identische Verzögerungen (kτ siehe Abb.14-5) hinzugefügt werden, ohne die Funktion zu beeinträchtigen.
In der Tabelle ist die jeweilige Schwingungsdauer als Delay eingetragen. Gehen wir davon aus, daß sowohl akustisch positive Peaks wie auch negative Peaks eine erhöhte Pulsfrequenz verursachen, so können die eingetragenen Delays auch halbiert werden.
Sind alle Zeitfunktionen auf ein Intervall {0...1} begrenzt, kann man für die Ausgabe y(t) in Näherung* schreiben
y(t) =
g1 x(t - τ1) +
g2 x(t - τ2) +
g3 x(t - τ3) +
gn x(t - τn)
mit y(t) = {0...1}; x(t) = {0...1} und gm = {0...1}.
Mit den synaptischen Gewichten
g1 = g2 = g3 = gn = 0,5
wird der Schwellwert 1 des Neurons bei jeweils zwei synchron ankommenden Impulsen erreicht.
(* Die Näherung besteht darin, daß die Pulsform der Ausgabe eines biologischen Neurons unabhängig von den Pulsformen der Eingaben ist.)
Ohne allzusehr in anatomische oder mathematische Details zu gehen: Das Soma des Neurons wird bei harmonischen Schwebungen in den Maxima mit einer höheren Wahrscheinlichkeit erregt und signalisiert damit: "Ich habe eine Harmonie entdeckt!".
Mit hoher Wahrscheinlichkeit wird dann die Ausgabe des Neurons etwa synchron mit dem Eintreffen der synchron ankommenden Maxima erfolgen, wobei nicht unbedingt angenommen werden muß, daß es synchron mit jedem Maximum pulst. Zwischendurch kann es sich Pausen gönnen (Refraktärzeit).
Denken wir abschließend darüber nach, ob dieser Interferenzkreis auch Harmonien in tieferer oder höherer Frequenzlage, aber mit gleichem Verhältnis detektieren kann, wie 12:8 = 3:2 (Quinte) oder 12:9 = 4:3 = 4:3 (Quarte) oder 4:3 oder 16:9 usw., dann hilft ein Blick auf die oben dargestellte vervielfachende Frequenzeigenschaft des Kammfilters. Es werden automatisch alle höheren Harmonischen betont, die tieferen leider nicht.
14.3 Fazit
Bliebe noch ein Fazit eines Entwicklers von mikroelektronischen Schaltungen und Schaltkreisen zu ziehen. Denken wir über den irrwitzigen Schaltungsaufwand nach, Harmonien mit digitalen Filtern zu erkennen - man denke an FIR, IIR (Finite Impulse Response, Infinite Impulse Response filter) und 32 Bit-Darstellung jedes Amplitudenwertes, dann beginnt man zu erahnen, warum diese Informatik der Natur so anders und in vielen Belangen so unglaublich viel effizienter arbeitet. Ein einziges Neuron mit einem Volumen von Kubik-Mikrometern übernimmt hier mit einem Energieverbrauch von Mikrowatt die Aufgabe, die technisch nur mit einem DSP (Digital Signal-Processor) mit vielen Watt und mit vielen Kubikzentimetern zu lösen ist. In der Tat: Wir sind noch sehr weit entfernt davon, diese Effiziens der Natur eines Tages in ganz ferner Zukunft erreichen zu können.
Kanalzahl und Raumdimension
Wie der vierbeinige Tisch oder Stuhl auf einer zweidimesionalen Ebene kippelt, so werden Interferenzorte durch Wellen aus unterschiedlichen Kanälen im Verhältnis zur räumlichen Dimension vorgegeben, siehe
Abb.14-2.
-
1-dim.: In eine einzelne Nervenfaser können wir zwei Zeitfunktionen von zwei Seiten einspeisen. Wir erhalten einen Interferenzort (Treffort der beiden Wellen) in Abhängigkeit vom Zeitpunkt der Einspeisung der Pulse. Das Experiment ist vom
Ischias-Nerv des Frosches bekannt. Beide Pulse fressen sich am Treffort auf, wo sie in die Refrakteritätszone des Gegners geraten. Mehr dazu siehe
Virtuelle Experimente.
-
2-dim.: Eine zweidimensionale Abbildung wird bereits mit drei Wellen bestimmt, nur drei Pulswellen besitzen auf der 2d-Fläche genau einen Treffort.
-
3-dim.: Eine dreidimensionale Abbildung wird am Treffort von vier Wellen
(Kanälen) fixiert.
Gehen wir induktiv weiter, so wird eine (nicht-überbestimmte) d-dimensionale Abbildung mit
k = d+1
(Dimensionssatz, Quelle: NI93)
Kanälen bestimmt, wobei d die räumliche Dimension darstellt.
Spezialfälle
k < d+1
Nutzen wir weniger als d+1 Kanäle, so entstehen wischende Abbildungen (mit deren Trajektorien können Bewegungsrichtungen z.B. auf der Haut oder im visuellen Cortex detektiert werden, siehe
Virtual Experiments or
[NI93], Kap.5, S.100.
k > d+1
Nutzen wir mehr als d+1 Kanäle, so entstehen überbestimmte Abbildungen (vgl. Abb.16-2). Wir sehen, das Bild wird am Rand unscharf (optische Abbildungen aller Art). Auch läßt sich ein überbestimmtes Bild nicht mehr so einfach bewegen, siehe Zoom oder Movement. Es ist robuster, als ein niederkanaliges Bild.
15.3 Zeitumkehr (Interferenzrekonstruktion)
Diese Überbestimmtheit trifft nur auf Projektionen (z.B. im Nervensystem oder in der Optik) zu. Nutzen wir exakt kompensierende, negative Delays wie bei der Akustischen Kamera, so können auch hochkanalige Abbildungen auf geringe Dimensionen abgebildet werden, da Überbestimmtheit durch den zeitlich kompensierenden Ansatz mit negativen Delays keine negativen Auswirkungen hat. Man denke an akustische Kameras: Hier werden z.B. 32 Kanäle genutzt, um auf einen zweidimensionalen Bildschirm abzubilden.
Im Nervensystem aber muss die Natur zu einem Trick greifen: wie in der Optik, können hier überbestimmte Abbildungen (k > d+1) prinzipiell nur durch Inhomogenität der Laufzeitgeometrie des Raumes in begrenzten Zonen scharf abgebildet werden
[NI93]. Siehe dazu auch
Abb.16-2, oben: Rekonstruktion, unten: Projektion von vier Kanälen auf einen zweidimensionalen Schirm.
15.4 Fazit
Ein körperlich dreidimensional aufgebautes Interferenznetzwerk kann
sich erst durch Inhomogenität als n-dimensionales Interferenznetzwerk darstellen. Mit vier Kanälen erhält ein Interferenznetzwerk z.B. die Möglichkeit, dreidimensional abzubilden oder zu speichern.
Es wird deutlich, warum wir im Laufe unserer Individualgenese erst durch Lehrer darauf aufmerksam gemacht werden müssen, daß eine für uns lebendige Welt aus Vergangenheit, Gegenwart und Zukunft besteht. Ein Interferenznetz benötigt ganze fünf Kanäle, um vierdimensional zu kartieren.
Auch dokumentiert sich hier der Unterschied zwischen Langzeit und
Kurzzeit-Gedächtnis. Es genügt zu erkennen, daß die physischen Grenzen des
Interferenznetzes (Kurzzeit-G.) irgendwo überschritten werden. Alles dannach muß anders gespeichert werden, zum Beispiel durch begriffliche Assoziationen
(Langzeit-G.).
Oder: Solange wir uns mit homogenen Netzen beschäftigen, kann
kaum Effiziens in der Informationsreduktion erwartet werden. Erst die zeitliche (Delays) und räumliche Inhomogenität von Netzen durch Kreuz- und
Querverbindungen eröffnet die faszinierenden Möglichkeiten des Nervensystems.
Ein Nachweis der Repräsentation höherer Dimensionen (Überbestimmtheit) könnte zum Beispiel erbracht werden, wenn es gelingen sollte, ein Signal gleichen Ursprungs auf einer Anzahl k verschiedener Fasern nachzuweisen, wobei k>4
sein sollte.
Gesetzt den Fall, wir bekommen hochkanalige Kanaldaten (Zeitfunktionen) irgendwo aus dem Nervensystem. Dann stellen sich zwei Fragen:
-
von welchen Orten des generierenden Raumes die Pulse kommen
-
an welche Orte im empfangenden Raum die Pulse gerichtet sind
Wir interessieren uns also für die Quellenzuordnung im Generator-Raum und für die Senkenzuordnung im Detektorraum.
Angenommen, wir bekommen Kanaldaten als Ableitungen der Axonen A und A' in folgendem Bild und vermuten, daß die Impulse von oben kommen.

Abb.16-1: Eindimensionale, neuronale Projektion (d=1, k=2). Emissionsorte im Generatorfeld oben und Hits im Empfangsfeld unten erscheinen spiegelbildlich zueinander. Nur erfolgreiche Hits mit einem Schwellwert nahe zwei sind dargestellt. Titelbild des Buches "Neuronale Interferenzen" 1993
[NI93].
-
Wollen wir aus den Kanaldaten die Emissionsorte im generierenden Raum berechnen, so sprechen wir von einer Interferenz-Rekonstruktion (Beispiel Akustische Kamera -
Link).
-
Wollen wir aus den Kanaldaten die Interferenzorte im empfangenden Raum erhalten, so sprechen wir von einer Interferenz-Projektion (Beispiel Bildgenerator für Chromatophoren von Tintenfischen -
Link).
Die Eigenschaften beider unterscheiden sich fundamental, obwohl sie nur ein Vorzeichen unterscheidet. (Kennen wir eigentlich: Minus 20 Grad fühlen sich anders an, als plus 20 Grad.)
Während die Rekonstruktion seitenrichtige Bilder liefert, die auch achsfern scharf sind, zeigt die Projektion typische Merkmale einer einfachsten optischen Kamera, bestehend aus nur einer Linse: Die Projektion ist nur axialnah scharf und liefert spiegelverkehrte Bilder.
Auch sind die Wellenfelder von Projektion und Rekonstruktion grundverschieden.
Projektion und Rekonstruktion unterscheiden sich nur in einem Vorzeichen, im Vorzeichen der zeitlichen Verzögerung τik der Kanäle.
Man vergleiche dazu den Algorithmus der Akustischen Kamera unter dem Link
(PDF german).
Die Zeit t und Delays τik mögen diskretisiert in Stützstellen vorliegen.
Für jeden zu berechnenden Raumpunkt pi(t) sind alle Kanäle
k entsprechend ihrer Verzögerung zu summieren. Zur Normierung wird schlußendlich durch die Gesamtzahl der Kanäle n geteit.
Die Berechnung der Zeitfunktion pi(t) des (Raum-) Pixel i für Rekonstruktion und Projektion unterscheidet sich damit nur im Vorzeichen der Delays τik.
Dieser winzige Unterschied im Vorzeichen markiert vollkommen andere Eigenschaften.
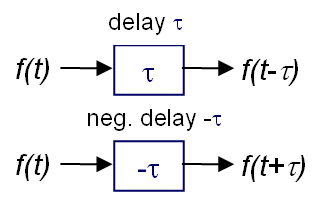
Bio-Interface alias PSI-Tools alias NoiseImage beherrschten nur den Algorithmus der Interferenz-Rekonstruktion mit kompensierenden (nichtkausalen) Verzögerungen (t + τik). Um damit eine Projektion berechnen zu können, wurde in PSI-Tools eine Funktion zur Zeitinversion aller Kanaldaten implementiert.
Um zu verstehen, warum sich damit alle Delays τik umkehren, erinnern wir uns an den Begriff der Verzögerungs- Maske (siehe "Virtuelle Experimente"
(PDF)).
Bei der Zeitumkehr der Kanaldaten wird aus jedem positiven Delay τik automatisch ein negatives Delay -τik und vice versa.
Berechnen wir damit einen akustischen Film, so entsteht dieser nun ebenfalls zeitlich rückwärts. Nachdem er fertig ist, haben wir ihn zeitlich rückwärts abzuspielen, um ihn vorwärts betrachten zu können.
Für Abb.16-2 wurde eine vierkanalige Projektion f(t-τ) und eine vierkanalige Rekonstruktion f(t+τ) (durch Zeitumkehr der Kanäle) mit Bio-Interface (später umbenannt in PSI-Tools) berechnet. Während die Rekonstruktion (oben) überall scharf ist, zeigt die Projektion (unten) die aus der Optik bekannte, nur axialnahe Schärfe. Auch erscheint sie - wie von optischen Linsenkameras bekannt, als Spiegelbild.

Abb.16-2: Oben: seitenrichtige Interferenz-Rekonstruktion. Unten: Spiegelbildliche Interferenz-Projektion mit achsferner Unschärfe. Quelle: Bionet96, Fig.13.
Zur Simulation beider Bilder wurde derselbe Satz Kanaldaten (Zeitfunktionen) genutzt. Der einzige Unterschied zwischen Rekonstruktion und Projektion (den Bildern oben und unten) ist eine Vorzeichenumkehr der vier Zeitfunktionen. Im oberen Teil schauen wir rückwärts in die Kanaldaten und erblicken das seitenrichtige "GH" des generierenden Feldes.
Im unteren Teil lassen wir die Zeitfunktionswellen zeitlich vorwärts über das Bildfeld laufen und erblicken damit ein spiegelverkehrtes "GH" als Interferenzintegral.
Abstrakt betrachtet, können wir Abb.16-2 in drei Teile teilen: Oben sehen wir den Generatorraum, der seitenrichtig abgebildet wird, mittig sehen wir die vier von oben nach unten fließenden Kanaldaten (Zeitfunktionen) und unten erkennen wir den Detektorraum mit dem spiegelverkehrten Bild.
a) 
b) 
Abb.16-3: Zugehörige Zeitfunktionen (Channel Data) zur
a) Rekonstruktion und zur b) Projektion (Software: PSI-Tools, 1995-1998).
Da ursprünglich nervliche Systeme analysiert werden sollten, war es wichtig, sowohl Rekonstruktion des Generatorraumes als auch Projektion in den Detektorraum zu verstehen.
Da wir mit 4 Kanälen auf ein 2-dimensionales Bild projizieren, ist die Projektion überbestimmt (für Bestimmtheit gilt: k = d+1; Kanalzahl k gleich Raumdimension d plus Eins), damit ist deren Ergebnis nur axialnah scharf.
Die Rekonstruktion ist zwar scheinbar auch überbestimmt, jedoch führt die perfekte Zeitinversion (durch negative Delays oder durch Zeitumkehr) dennoch zu einer perfekten, niemals überbestimmten Abbildung (auf allen Wegen herrscht identische Verzögerung) - das war eine der Grundideen, die zum Rekonstruktionsalgorithmus der ersten, "Akustischen Kamera"
(Link) führten. Die zweite wesentliche Grundidee war die, daß nur durch Zeitinversion ein seitenrichtiges Bild entstehen kann.
a)  b)
b) 
Abb.16-4: Wellenfelder a) der Rekonstruktion (Typ f(t+τ)) und b) der Projektion (Typ f(t-τ)). Man erkennt die Zeitinversion der Interferenz-Rekonstruktion (links) sofort: Wellen laufen "unnatürlich" einwärts mit der Wellenfront innen und dem Schwanz außen.
Abb.16-2 wurde aus einer Rekonstruktion (oben) und einer Projektion (unten) derselben Kanaldaten auf einen identischen Detektorraum erzeugt.
Der Unterschied zwischen spiegelverkehrter Interferenz-Projektion und seitenrichtiger Interferenz-Rekonstruktion besteht in der invertierten Zeitrichtung. Die Rekonstruktion zeigt die Quellorte des Generator-Raumes, die Projektion die des Detektor-Raumes.
Aber Bio-Interface, wie PSI-Tools, wie auch NoiseImage können nur (seitenrichtige) Rekonstruktionen berechnen. Um das Wellenfeld einer Projektion zu berechnen, hat man die Zeitfunktionen vor der Rechnung zu invertieren Abb.16-3,
aus f(t+τ) wird f(-t-τ).
Dann wird der Film berechnet. Da aber jetzt die Zeitrichtung der Bildfolge invertiert ist, ist die Bildfolge des Films danach wieder zu invertieren. Erst dann erscheint das Wellenfeld der Projektion, Abb.16-4 b).
Es verdeutlicht das Wesen neuronaler Abbildungen. Während die (unnatürliche) Rekonstruktion ungestört und seitenrichtig erscheint, sehen wir die Projektion verzerrt (überbestimmt) und seitenverkehrt. Wir erinnern uns, daß auch zeitlich vorwärts laufende, optische Projektionen spiegelverkehrt sind und nur in Achsnähe scharf erscheinen.
Ist die Abbildung überbestimmt, können Mehrdeutigkeiten am
Interferenzort entstehen. Die Projektion zeigt, daß im Bereich um die zentrale Symmetrieachse eine hohe Bildqualität durch hohe Übereinstimmung der Laufzeiten auf allen Pfaden erreicht wird. Am Rand stimmen die Delays der vier Kanäle nicht mehr ganz so genau überein, hier wird das Bild unscharf.

Abb.16-5: PSI-Tools berechnet eine Projektion. Weil PSI-Tools nur Rekonstruktionen rechnen kann, wurden die Zeitfunktionen (channel data) vorab zeitlich invertiert, um eine Projektion zu berechnen. Zu finden als letzte Demo in psi.zip
Aus der Betrachtung wird eine weitere Besonderheit von Pulsinterferenzen sichtbar: Eine (weder unter- noch über-) bestimmte Abbildung k = d+1 erlaubt nur spezifische Zeitfunktionen mit langen Pausen. Bei Nervenzellen nennt man das Refraktärzeit. Da Abbildungen bei vorwärtslaufender Zeit (Projektionen) im Nervennetz nicht beliebig überbestimmt sein können, war die Natur gezwungen, den Zeitfunktionstyp vom Dirac-Typ für bildgebende Informationsverarbeitung zu entdecken.
Die Bilder und Filme der akustischen Kamera (nahezu sinusförmige Zeitfunktionen) hingegen bedurften eines anderen Tricks: hier werden negative Verzögerungen f(t+Τ) verwendet, um positive Delays f(t−Τ), Weg von der Quelle zurück zu den Mikrofonen) zu kompensieren. Den entsprechenden Algorithmus nannte ich noch 1993
Maskenalgorithmus
(siehe den Animationsfilm
Fig.8 dazu) sowie die
Interferenzrekonstruktion.
Nur zur Erinnerung: Eine (positive) Verzögerung (+Τ) verschiebt eine Zeitfunktion mit f(t−Τ). Eine zur Kompensation einer Laufzeit benutzte (nicht kausale) negative Verzögerung (−Τ) verschiebt eine Zeitfunktion mit f(t+Τ).
Negative Verzögerung hieße eigentlich, die Wirkung erscheint vor der Ursache (nicht kausal). Das geht natürlich nicht. Wir benötigen immer noch eine hinreichend große, globale Verzögerung aller Kanäle (z.B. durch Zwischenspeicherung), um negative Verzögerungen ausführen zu können.
Bleibt zum Schluß noch eine ganz wesentliche Frage: Wäre ein reales Nervennetz oder eine reine Hardware ebenfalls imstande, Rekonstruktionen auszuführen?
Dazu erinnern wir uns daran, daß die Rekonstruktion mit negativen Delays arbeitet. Diese sind nichtkausal: Deren Wirkung tritt vor der Ursache ein.
Während die Kanaldaten bei der Akustischen Kamera gespeichert vorliegen - und wir Daten von beliebigen Zeitpunkten abgreifen können, sowohl welche aus der Vergangenheit als auch aus der Zukunft, haben Hardwarelösungen eine Einschränkung: Sie können nur aus der Vergangenheit Zeitpunkte abgreifen.
Allerdings gibt es auch dafür eine einfache Lösung: Man verlagere durch Addition einer zusätzlichen Verzögerungszeit auf allen Kanälen die Berechnung der Bildpunkte in die Vergangenheit. Wenn dieses Delay größer der größten Einzelverzögerung ist, sind auch Berechnungen von Rekonstruktionen in Hardware möglich.
Der Begriff "Beamforming" (Strahlformung) stammt wohl von Frequenz- begrenzter Hardware im Bereich von RADAR bis SONAR der 1930er Jahre. Bei den Phased Arrays schwenkte man den Strahl zum Beispiel durch LC-gekoppelte Antennen oder Aktoren. Eine kleine Phasenveränderung verzögert dabei die Phasenlage zwischen den Antennensegmenten und schwenkt den Strahlwinkel einer festen Frequenz. Man hatte und brauchte kein nichtkausales, negatives Delay. Entsprechend dachte wohl auch niemand über das entscheidende Vorzeichen nach. Man schrieb einfach f(t - τ) für ein verzögertes Signal. Daraus aber entsteht eine I.-Projektion, die genau genommen, spiegelverkehrte Bilder liefert.
Nun wird man mit beiden Konzepten, mit der Interferenz- Projektion wie mit der Interferenz- Rekonstruktion, einen Beam erzeugen, auch wenn deren Bildeigenschaften vollkommen verschieden sind.
Im Nervensystem sind beide Ansätze nötig, um einerseits in den Generatorraum zurückzurechnen mit einer Rekonstruktion
Abb.16.2 oben, und um andererseits in den Detektorraum vorwärts zu rechnen mit der Projektion,
Abb.16.2 unten.
In technischen Bereichen (akustische Bilder, Sonar, Radar) kann man eher keine spiegelverkehrten Bilder gebrauchen, hier kommt wohl ausschließlich die Rekonstruktion zum Einsatz.
Auch sind Probleme mit akustischen Bildern im Vergleich zum RADAR von anderer Natur. Wir hatten ein limitiertes Set von Mikrophonarray- Hardware (Star, Ring, Cube u.a.), einen großen Frequenzbereich der Objekte mit sehr verschiedenen Wellenlängen (100 Hz ∼ 3,4 m bis 100 kHz ∼ 3,4 mm); zu kartierende Maschinen variieren stark in deren Größe von Zahnbürste bis Großbagger und einzelne Quellen der zu kartienden Objekte strahlen in verschiedene Richtungen. Hier ist ein großer Erfahrungsschatz nötig, um über die Wahl des Arrays und über die richtige Entfernung die richtige Apertur (Öffnungswinkel) zu treffen. Auch sind zu kartierende Objekte meist von allen Seiten zu kartieren, um wesentliche Emissionsrichtungen der Teilquellen erkennen zu können. Nicht zuletzt stehen die Objekte oft in geschlossenen Räumen mit erheblichen Raumresonanzen. Beamforming- Theorie hilft hier wenig weiter.
Bis zum Gelingen unseres ersten, akustischen Standbildes 1994 ist dem Autor nachträglich nur ein Aufsatz bekannt geworden, der das richtige Vorzeichen
(f(t + τ)) verwendete: Brühl, S., Schmitz, K.-P.: Noise Source Localization on Highspeed Trains using Different Array Types. Internoise1993, Leuven, Aug.24-26, 1993. Brühl und Schmitz zeigten hier ein allererstes akustisches Bild, es war das Abrollbild (sog. Linescan) eines Transrapid, der an einem Stab-Array vorbei fährt.
Das mag eine Erklärung dafür sein, warum gerade dem Team Heinz/Höfs/Busch von 1994 bis 1996 erste, akustische Standbilder weltweit gelangen.
Alle mir bekannten, maßgeblichen Fachbuchautoren (z.B. Johnson/Dudgeon: Array Signal Processing, Prentice Hall 1993, p.112/113 "4.1 Delay and Sum Beamforming") verwendeten damals unwissend das falsche Vorzeichen (minus) in f(t - τ), auch wenn sie sich mit Interferenz-Rekonstruktion mit kompensierender, rückwärtslaufender Zeit, beschäftigten. Wollte man ein seitenrichtiges, akustisches Bild rechnen bekam man stattdessen eine spiegelverkehrte Projektion.
Damals wußte noch niemand, wie ein akustisches Bild aussehen kann. Weder kannten wir Aliasing oder Raumresonanzprobleme der Objekte, noch waren wir bei den technischen Parametern der Arrays oder Datenrecorder sattelfest.
Die im
Bio-Interface (später
PSI-Tools) zu lösenden Software- und Hardware-Probleme waren komplex genug, um an winzigen algorithmischen Fehlern scheitern zu können. In dieser Situation genügt ein falsches Vorzeichen in der Software, um alles hinzuwerfen.
Aufgrund dieser fatalen Situation ist der Begriff des Beamforming für mich nicht hilfreich. Er sollte gemieden werden, weil er durch zu viele spezielle RADAR- und SONAR- Probleme belastet ist. Das möge erklären, warum der Autor die Begriffe der Interferenz-Rekonstruktion und der Interferenz-Projektion einführte und deren Verwendung noch immer nur empfehlen kann.
Bislang wurden viele Grundlagen erörtert. Aber wozu ist das alles gut? Warum kam C.S. Peirce schon vor 150 Jahren zur Feststellung "All thought is in signs" (alles Denken ist in Zeichen)? Können wir Zeichen mit der Theorie der IN erkennen?
Im Vergleich zum Computer arbeitet unser Gehirn grundverschieden.
Jeder von uns, der 23 mal 4 rechnen kann, kann es bemerken: Wir stellen uns vor, wieviel 20 mal vier ist und wir stellen uns vor, wieviel 3 mal 4 ist. Auch können wir in unserer Vorstellung 80 und 12 addieren.
Nun haben wir schon im Kapitel 11, Bild 8 gesehen, daß Interferenzorte auch an unerwarteten Stellen entstehen können und dort Zeichen (gh) detektieren.
Im Buch Neuronale Interferenzen [NI93] wurde im Kap.5 unter den Überschriften "Merkmalsextraktion" S.111 und "Detektion von Geometrien" S.115 eine andere, schon fast vergessene Möglichkeit beschrieben, wie Interfernznetze in einfacher Art und Weise über relative Laufzeiten Zeichen, Buchstaben, Formen oder Bilder detektieren könnten.
Denken wir an die sechs Neuronenlagen des Visuellen Cortex,
(Link)
dann wird klar, daß noch viele, zielführende Ideen erforderlich sind, um die Funktion des visuellen Systems
(Link)
eines Tages inhaltlich untersuchen und verstehen zu können.

Abb.17-1: Detektion eines Buchstaben "B" (Quelle: "Neuronale Interferenzen" 1993 [NI93], Kap.5, S.115). Der Hauptdetektor d signalisiert, daß im Feld ein "B" zu erkennen ist. Die im Bild eingezeichneten Radien dienen nur der Veranschaulichung der etwa streckenproportionalen Laufzeit, gleichen Neuronentyp vorausgesetzt.
Wir nehmen an, wir richten den Blick auf eine weiße Fläche mit einem kleinen "B". Dieses "B" wird vermutlich gespiegelt und im Hell/Dunkel-Kontrast invers irgendwo im visuellen Cortex (VC) erscheinen. "Belichtete" Neuronen könnten dort anfangen zu feuern.
Synchrones Feuer der Kanten des "B" vorausgesetzt, würden Neuronen an den Orten a, b, c je etwa gleichzeitig befeuert, was diese erregen sollte.
Dazu nehmen wir der Einfachkeit halber an, daß die Verbindungsleitbahnen zwischen allen Neuronen bidirektional sind. Feuert jetzt durch einen Zufall Neuron d, dann könnten a, b, c ebenfalls erregt werden und feuern.
Die im betrachteten Bildfeld liegenden Neuronen, die vom "B" (invers oder tatsächlich) belichtet werden, könnten nun ihrerseits feuern und wiederum a, b, c erregen.
Wenn Neuron d etwa denselben zeitlichen Abstand von a, b, c hat, dann dürfte Neuron d nun ebenfalls feuern: Dieses Neuron d würde das "B" im Sichtfeld erkennen und signalisieren.
Gleiche Pulsbreiten vorausgesetzt, ist die Abbildungsqualität (wie in der Optik) von der Entfernung abhängig, siehe
die Simulationen zur Abstandvariation.
Das erfordert, daß sich Neuron d in der Nähe von a, b, c befindet.
Wir könnten sogar noch einen Schritt weitergehen, wenn wir an die nach links gerichteten Serifen des "B" denken, die die Erkennung der senkrechten, geraden Kante durch Neuron a erleichtern.
Die Art einer Selbstsynchronisation der Neuronen a, b, c mit den Kanten des "B" sowie von a, b, c mit d kann durch wechselseitiges Ping-Pong-Spiel erfolgen. Der zeitliche Abstand möge in Summe dt betragen, der räumliche entsprechend ds = v/dt.
Man denke dabei an die von
Wolf Singer untersuchte Synchronität im VC in seinen
Katzenexperimenten.
Wenn wir etwa die Leitgeschwindigkeit v der Neuronen kennen,
dann wäre ein Maß für den Abstand zwischen dem Feld und Neuron d (über die Neuronen a, b, c) die auftretende (meßbare) Synchronisationsfrequenz f entsprechend v = ds/dt und daraus
f = 1/dt = v/ds
Denken wir an die Vorteile der Singerschen Ping-Pong-Synchronisation, so kommt der dadurch vergrößerten Pulspause eine entscheidende Bedeutung zu.
Wiederholen wir diesen Versuch für andere Buchstaben, Ziffern oder Zeichen, so ist zu erkennen, daß in der untersten Ebene von Neuronen jeweils nicht mehr als etwa vier Neuronen gebraucht werden, um ein lateinisches Zeichen zu erkennen, siehe das folgende Bild.

Abb.17-2: Detektion der Ziffern 1 und 0 (oder des Buchstaben O) mit jeweils vier Detektorneuronen in der ersten Ebene. Quelle [NI93], Kap.5, S.116
Wenn wir an die irwitzige Menge von Figuren, Zeichen und Bildbestandteilen denken, die von uns im Alltag erkannt werden müssen, sind wir schnell bei ein paar Millionen Neuronen, die für Detektorneuronen zu reservieren sind. Insofern ist eine minimalistischste Variante der Verschaltung auf der Ebene der Detektorneurone recht wahrscheinlich.
Fragen wir noch danach, wie der VC das u.U. windschiefe, zu große oder zu kleine oder nicht sauber im Bild liegende "B" ausrichten und skalieren kann, so denke man z.B. an die Funktion der Glia für
Zoom und Movement.
An dieser Stelle ist noch darauf hinzuweisen, daß die hier gezeigte Art der Detektion im Gegensatz zu Kap.11, Bild 8, eher unflexibel wäre, weil zu viele ortsfeste Detektorneuronen gebunden würden. Da allerdings letztlich das "B" irgendwo als Buchstabe erkannt werden muß, wäre realistisch ein Zwitter aus Interferenzkreis und Detektorneuronen zu erwarten.
Wir wissen, daß bereits in der Sehbahn für eine Zentrierung und Skalierung mit Zoom und Movement des Bereichs höchster Sehschärfe auf ein kleines Gebiet erfolgt, in welchem sich dann die hier gezeigten Anordnungen befinden.
Stellen wir zum Schluß noch die bedeutsamste Frage der Informationsübertragung im Nervensystem überhaupt:
Warum erregen sich fast einhundert Milliarden dicht gedrängt und billionenfach verbundener Neuronen im Cortex nicht permanent gegenseitig? Was hindert unmittelbare Nachbarn daran, sich permanent zu befeuern? Warum gibt es keinen totalen Kurzschluß aller Informationen?
Wenn der Cortex ein Netzwerk wäre, das nur mit Gewichten arbeitet (künstliche neuronale Netze, Hebb'sche Netzwerke...), dann wäre dies theoretisch denkbar.
Um die Frage zu klären, haben wir uns klarzumachen, welche Rolle Verzögerungen von Dendriten und Axonen, im Soma und in Synapsen spielen.
Da Neuronen sehr viele Synapsen besitzen (Eccles spricht von bis zu siebentausend für Pyramidalneuronen) kann Kommunikation nur effektiv funktionieren, wenn eine Übertragung auf sehr vielen Pfaden in Gleichzeitigkeit passiert (Bedingung für Selbstinterferenz, wie für Fremdinterferenz), egal ob sich innerhalb der Pfade weitere Neuronen befinden.
Angenommen, wir haben zwei Neuronen (nahezu) identischer geometrischer Form, die extrem dicht nebeneinander liegen und die mehrfach miteinander verbunden sind. Könnten sie sich selbst erregen? Wir wollen diese zwei Neuronen mit P und P' bezeichnen. P soll senden und P' soll empfangen.
Die Neuronen seien durch Synapsen an den Stellen AA' bis DD' miteinander verbunden, Abb.18-1. Neuron P soll versuchen, Neuron P' zu erregen.
Entscheidende Bedingung dafür ist ein hoher Schwellwert von P' (hier nahe vier), d.h. vier Pulse müssen gleichzeitig bei P' ankommen, um P' zu erregen.
Vorausgesetzt wird, daß die Leitbahnen (PA = P'A') bis (PD = P'D') sehr verschieden lang voneinander sind.
Damit aber sind auch die Delays von (PA, P'A') bis (PD, P'D') sehr verschieden.
Ein gleichzeitiges Ankommen der vier Pulse von P bei P' ist damit ausgeschlossen.
Im Timing-Diagramm von Abb.18-1 ist das zu erkennen. Man sieht, daß das Delay PA sehr verschieden von A'P' sein muß, wenn die Neuronen miteinander kommunizieren wollen. Das aber widerspricht den geometrischen Gegebenheiten.
Führen wir den Begriff der Maske M für Neuron P und M' für Neuron P' als Vektoren ein,
M = {PA PB PC PD}
M' = {P'A' P'B' P'C' P'D'}
dann gilt, daß die Komponenten beider Masken in vektorieller Addition den Wert der Gesamtverzögerung τ haben müssen:
T = τ {1 1 1 1}
M + M' = T
Während die Geometrie identisch ist, sind die Masken komplementär zueinander, siehe Timing in Abb.18-1. Um den Begriff der "Maske" besser zu verstehen, schaue man sich eine Animation zum Maskenalgorithmus
Fig.8 an.

Abb.18-1: Zur Übertragung einer Erregung müssen die Masken M und M' beider Neuronen P und P' exakt komplementär sein, M + M' = T. Das aber widerspricht hier den geometrischen Gegebenheiten, siehe Bild. So muß z.B. das Delay PA i.a. sehr verschieden von A'P' sein, wenn die Neuronen miteinander kommunizieren wollen. Bildquelle: page 5 at
BioNet'96: Third Workshop 'Bio-Informatics and Pulspropagating Networks', 14.-15. Nov. 1996, GFaI Berlin, ISBN 3-00-001107-2
Zwei dicht benachbarte Neuronen, die an verschiedenen Stellen miteinander verbunden sind, können folglich nicht miteinander kommunizieren, wenn beide Neuronen geometrisch identische Masken M = M' besitzen. Was sie für eine Kommunikation benötigen, wären komplementäre Masken, M' = T - M, siehe Bild. Das aber ist geometrisch ausgeschlossen. Siehe dazu auch die Animation
Fig.7, die das Problem verdeutlicht.
Dort, wo das eine Neuron eine längere Leitbahn (Dendrit oder Axon) zum Nachbarn besitzt, müßte der Nachbar entsprechend eine kürzere Leitbahn aufweisen, um auf mehreren Kanälen Gleichzeitigkeit zu wahren.
Dieses Prinzip verhindert letztlich ein ungewolltes Überspringen von Erregung zwischen benachbarten Neuronen und den totalen Zusammenbruch aller Informationsübertragung.
Man könnte sagen, die Erregung kann von ihrer dynamischen Natur her kaum zwischen zwei identischen, an gleiche Ortsknoten angeschlossenen Neuronen überspringen.
Der mathematische Hintergrund wird auch im Kap.4 von "Biomodelle" gestreift
(english,
german).
Beziehen wir Fremdinterferenzen mit ein (Kap.14.2), wird der Sachverhalt komplexer. Hier hätten wir die Schwingungsperioden zusätzlich zu berücksichtigen, wodurch sich verschiedene geometrische Konstellationen eignen, um eine Kommunikation dicht benachbarter Neuronen dennoch zu ermöglichen.
Ein historisch erster Beleg für diese Eigenschaft ist im Kap.10, S.210/211 im Buch "Neuronale Interferenzen" (1993) zu finden
(german,
english).
Am Anfang stand 1993 die Hoffnung, erste "Bilder der Gedanken" aus spikeartigen Zeitfunktionen des Nervensystems machen zu können.
Einige ungewöhnliche Bilder entstanden tatsächlich aus einem ECoG - leider unter Zeitdruck und später nicht mehr reproduzierbar:
Bild 12, Bild 13.
Da niemand Interferenzintegrale im Kopf berechnen kann, war eine Software zu entwickeln. Diese wurde konsequenterweise "Bio-Interface" genannt. Sie sollte aus Bitmaps Zeitfunktionen generieren, aus Zeitfunktionen Interferenzintegrale berechnen können, sowie Zeitfunktionen aufnehmen können. Außerdem waren Kanaldaten darzustellen und Zeitfunktionen zu invertieren, um spiegelnd/nicht spiegelnd (Projektion/Rekonstruktion) rechnen zu können. Dieser minimale Funktionsumfang war erforderlich, um das Werkzeug mit sich selbst testen zu können.
Im Gegensatz zu ANN-Simulatoren wurden (ungehinderte) Wellenausbreitungen über zwei Felder (Generator und Detektor) berechnet. Es war kein (artifical) Neuro-Simulator, eher ein Wellenfeld-Simulator. In jedem Pixel des Detektorfeldes wird das Interferenzintegral aller Kanäle berechnet. Es gab keine Möglichkeit, refraktive Auslöschung einzubeziehen.
Als klar wurde, daß keine Möglichkeit besteht, qualitativ geeignete, hochkanalig-spikende Ableitungen aus Nervenfasern zu erhalten, andererseits mit dem "Bio-Interface" erste akustische Bilder entstanden waren, wurde der Name Anfang 1996 neutralisiert und umbenannt in "PSI-Tools" (Parallel and Serial Interference Tools). Es begann die Ära erster, akustischer Bilder und Filme. Die Arbeit an Nervennetzen verblaßte.
Ab 1998 wurde PSI-Tools weiterentwickelt und auf akustische Bilder fokussiert, etwa ab 2000 hieß es "NoiseImage". Es erhielt einen USB-Kameraanschluß zur automatischen Überlagerung des akustischen Bildes auf das optische Bild, dafür entfielen andere Möglichkeiten, wie die Zeitumkehr der Kanaldaten oder die verschiedenen Rechenalgorithmen.

Abb.19-1: Bio-Interface: Ur-Werkzeug, mit dem erste Interferenzabbildungen simuliert wurden und mit dem die ersten akustischen Bilder und Filme entwickelt wurden (Sabine Höfs und Gerd Heinz).
Der pink gekennzeichnete Weg oben zeigt von rechts nach links die Kanaldatensynthese aus Bitmaps. Der neongelbe Weg unten zeigt von links nach rechts die Entwicklung der Bilder aus gemessenen Kanaldaten.
Die Interferenztransformation konnte in einem Detektorraum mit beliebig wählbarer Kanalanordnung ausgeführt werden. Bio-Interface/PSI-Tools konnte nur die seitenrichtige (aber zeit-inverse) Interferenz-Rekonstruktion berechnen. Zur Berechnung von spiegelbildlichen Interferenz-Projektionen konnten alle Kanäle zusätzlich zeitinvertiert werden.
Damit entsteht zwar ein rückwärtslaufender Film, der aber kann nachträglich wieder rückwärts abgespielt werden, sodaß auch Filme von Projektionen zeitlich richtig herum erstellt werden können. Die Urversion des Bio-Interface spuckte nur Bitmaps-Serien (*.BMP) als Film aus, die Zusammenstellung zum Film (*.GIF, *.AVI) erfolgte mit einem separaten Progrämmchen, dessen Zählrichtung man auf inkrement oder dekrement stellen konnte.
Zu Testzwecken und für allgemeine Simulationsaufgaben wurde zusätzlich eine
Kanaldatensynthese ausgehend von einem als Bitmap vorliegenden Generatorfeld (siehe Abb.5-1)) implementiert.
Mit angeschlossener Hardware war es möglich, hochkanalige Datenströme aufzuzeichnen. Funktionen der Hardware waren digital einstellbar und speicherbar. Die Verstärkung konnte über 5 Zehnerpotenzen variiert werden, beginnend bei 500µV Vollausschlag. Hardware-Hochpaß und -Tiefpaßfilter gestatteten Aufnahmen in einem wählbaren Bereich von 0,05 Hz bis 50 kHz. Die Kanalverstärker waren für hochohmige Quellen (15 kOhm/EEG) rauschoptimiert.
Bio-Interface/PSI-Tools arbeitete seit 1994 mit einem 16 Kanal-Datenrecorder UEI-DAC WIN30-DS von UEI (Vertrieb über National Instruments, ISA-Board). Vorverstärker wurden selbst entwickelt, siehe Bilder der Hardware von damals.
Versuche mit Labwindows eine GUI zu bauen, wurden abgebrochen. Labwindows war zu langsam. Sabine Hoefs entwickelte Bio-Interface/PSI-Tools unter Borland-C (Windows3.11) weiter. Etwa gegen 1995 wurde auf Microsofts MS-C unter Windows95 umgestellt.
Siehe auch eine Beschreibung mit Bildern und den alten Help-Files der
Software sowie der
Funktionen mit Download-Möglichkeit von PSI-Tools. Mit der Software wurden verschiedene
Verifikationen
möglich.
Zur Klärung dieser Frage sehen wir uns bitte nochmals
Abb.2-3 an. Wie ist es möglich, die nach unten gehende Projektion zu verändern, sie auf ein anderes Empfangsfeld zu richten?
Offenbar zum Beispiel dadurch, daß Zooming-
(Kap.6) und Moving-Effekte
(Kap.10) genutzt werden. Dazu können die Verzögerungszeiten auf A oder A' verändert werden. Ebenso ist denkbar, daß erregte Neuronen im Empfangsfeld wiederum Generatorneuronen eines weiteren Interfernenzkreises darstellen. Nicht zuletzt ist es sehr wahrscheinlich, daß Generatorneuronen in den Knoten der Hologramm-Muster
(Kap.7) liegen, die sich zwangsläufig aus Fremdinterferenzen
(Kap.8) ergeben. Damit wären komplexe Lauterkennungen möglich.
Nun sind wir es gewohnt, in Schaltungsblöcken zu denken, die jeder für sich eine separate Aufgabe erfüllen. Aber an den obigen Beispielen ist abzulesen, daß diese Art und Weise strukturierten Denkens auf Nervennetze nicht anwendbar sein wird. Jede Nervenzelle, jede Verbindung kann in dutzende oder hunderte völlig verschiedener Aufgaben eingebunden sein, über nur die Struktur der Verzögerungszeiten entscheidet. Hier sind revolutionäre, neue Ideen gefragt.
Wir sehen, daß vor der Neuroforschung noch gewaltige Aufgaben stehen, ehe wir annähernd so weit sind, "Bewußtsein" oder "Nachahmung" verstehen zu können. Interferenznetze liefern erst einmal nur die physikalische Basis, auf der weitergebaut werden kann.
Ich wünsche allen jungen Menschen, die sich dieser Forschung verschreiben, alles Beste! Lassen Sie sich nicht durch abgelehnte Förderanträge oder fehlende Mittel beeindrucken, wenn Sie ein Ziel zu erkennen glauben!
Wo ein Wille ist, ist auch ein Weg!
Dank an alle, die an Bio-Interface/PSI-Tools mitarbeiteten und viel Initiative einbrachten, um den ersten Interferenzsimulator zu entwickeln. Besonderen Dank an unsere fleißige 'Biene', Sabine Höfs (geb. Schwanitz), die Bio-Interface/PSI-Tools programmierte und damit die Grundlagen einer "interferenziellen Neuroinformatik" wie auch die der "akustischen Photo- und Kinematographie" überhaupt erst ermöglichte. Dank an Dirk Döbler, der den verkaufsfähigen Rekorder entwickelte, PSI-Tools optimierte und die USB-Kamera in NoiseImage integriert hat. Nicht zuletzt besonderen Dank an Carsten Busch, Sven Tilgner und Nico Matschiner, die die jeweiligen Hardwareentwicklungen in die Kleinserie umsetzten.
Gerd Heinz
* Auf diese Seite wurden ursprünglich interessante Bilder für Presse oder Kollegen gestellt. Dies möge die spärliche Kommentierung und das teils spartanische Aussehen rechtfertigen. Weil die Seite aber einen knappen, teils prosaischen Überblick bietet, soll sie halt bleiben.
** Ursprüngliche Absicht war es eigentlich, das griechische Wort holos für 'ganz' in das lateinische totos für 'ganz' zu übersetzen. Dies scheiterte offenbar am verwendeten Wörterbuch. Aber ein Kind braucht einen Namen.
Mail send?
File created Sept.1, 1995
Continuous edited
Redesign March 2013
HTML-redesign and some adds October 2020
English translation using https://translate.google.com since June 12, 2021
Thanks to the Google team, the translation becomes more and more very helpfull!
Stylesheets and remarks January 2024
Kap.3.2 added November 2024
Visitors since Dec. 2021:




 Wie ist es möglich, daß eine zwei Millimeter große Fruchtfliege Drosophilidae
(Wikipedia), deren Cortex vielleicht einen zehntel Millimeter groß ist, sich im Raum orientieren kann, ihre Flügel kontrolliert, Nahrung findet und sich vermehren kann? Können wir mit unserer Mikroelektronik und Informatik jemals in diesen Bereich vorstoßen? Oder hat die Natur viel effizientere Möglichkeiten, als wir?
Wie ist es möglich, daß eine zwei Millimeter große Fruchtfliege Drosophilidae
(Wikipedia), deren Cortex vielleicht einen zehntel Millimeter groß ist, sich im Raum orientieren kann, ihre Flügel kontrolliert, Nahrung findet und sich vermehren kann? Können wir mit unserer Mikroelektronik und Informatik jemals in diesen Bereich vorstoßen? Oder hat die Natur viel effizientere Möglichkeiten, als wir?

































 b)
b) 







