1 Auditory localization of the barn owl
2 First neural interference circuits
3 Why were the delays forgotten?
4 An intelligent substrate
5 What characterizes an interference circuit?
6 Simulator and measuring device
7 Reconstruction versus projection
8 Wave field of a projection
9 Images of thoughts
References
According to a paper of Masakazu "Mark" Konishi [1], Lloyd A. Jeffress [9] gave a basic circuit in 1948 , which describes the acoustic location principle of barn owls (Figures 1 and 2). It is Mark Konishi's credit for popularizing the Jeffress approach in June 1993. Coincidentally, the book "Neural Interference" had just been finished. However, the article came too late for research into the nervous system. The ANN had already begun its unstoppable triumph.
This fundamental circuit, today we would call it an "intermedial interference circuit", shows important features of biological informatics in a new perspective: a correspondence between a place and the transmitting time functions, a connection between code in space and time.
Regarding Jeffress Figure 2, Mark's version in Figure 1 represents a simplified version of Jeffress. Unfortunately, both wrote about low tones and (sinusoidal) sound waves instead of pulse-like time functions. In the inner ear, sounds are converted into density-modulated pulse sequences.
The problem is the emergence of cross-interference patterns (aliasing) that can completely prevent the ability to locate a source, see simulations for pulse sequences or sine waves. Pulse density modulated signals are clearly advantageous here.

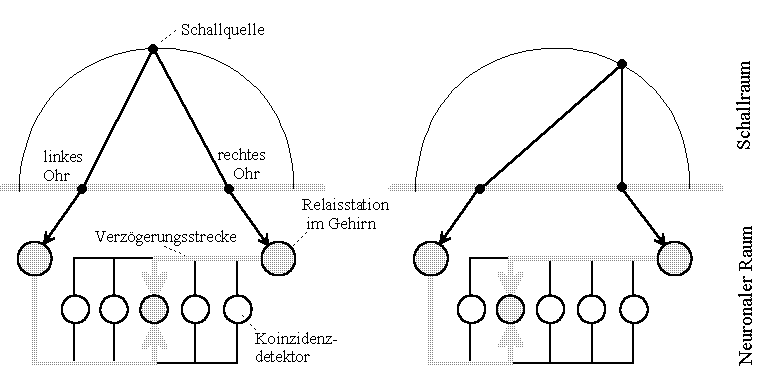
Fig.1: Simplified hearing model of a barn-owl from Konishi, 06/1993 [1]. Translation: "Schallquelle" sound source, "linkes Ohr" left ear, "rechtes Ohr" right ear, "Relaisstation im Gehirn" relais station in the brain, "Verzögerungsstrecke" delay line, "Koinzidenzdetektor" coincidence detector, "Schallraum" sound space, "Neuronaler Raum" neural space.
The function: If a sound source lies on the line of symmetry between both ears, the noise-signals converted into nerve impulses in the ear ("Relaisstation" ~ relay station) reach neurons ("coincidence detector") in the middle of the brain at the same time. However, if the source is offset to the right, the nerve impulses meet further to the left in the brain. Let us now multiply those coming from the left and right on each neuron, i.a. With time-shifted time functions (Mark Konishi put it more complicatedly), only the neuron in which the signals appear at the same time is excited (highlighted). For the neuron, a multiplication with the abstraction is sufficient, assuming the pulse value to be one and rest periods to be zero.
We discover the following properties of an interference circuit (see also [6], [7], [ 8]:
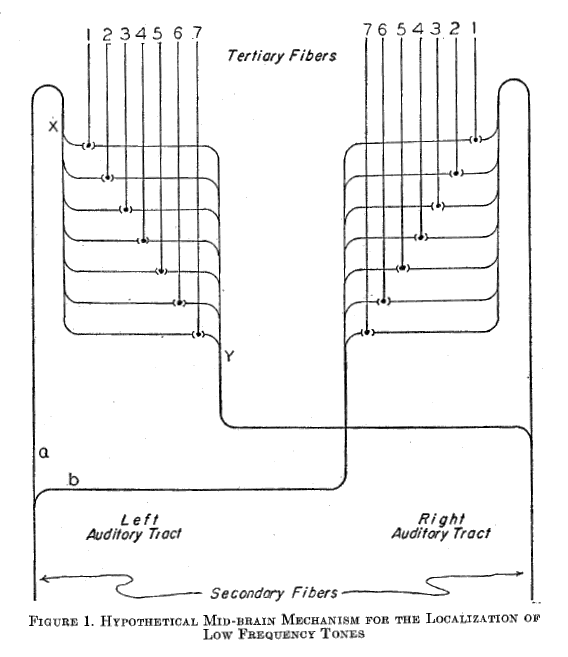
Fig.2: Illustration by Jeffress 1948 [9] - historically the birth of neural interference circuits.
Jeffress and Konishi's interpretations unfortunately refer to sinusoidal time functions known from acoustics that are unsuitable for modeling the nervous system. Jeffress's caption "low frequency tones" is also questionable.
The acoustic camera shows, that the wavelength λ determines the spatial resolution. A frequency f of 100 Hz corresponds to a wavelength λ of 3.4 meters; 1 kHz is 34 cm; 10 kHz is 3.4 cm; 100 kHz is 3.4 mm (λ = v/f at an acoustic conduction speed v of 340 m/s).
The higher the frequencies, the better the localization. High-frequency rustling can be located much more precisely than low tones. Neurons in the inner ear also generally emit very short, pulse-like signals. See also a simulation of a 3-channel, sinoidal wave interference, which makes the finding of the source impossible.
Video 1: Animation of the first interference circuit, interpretation by the author. Souurce: Jeffres L. A.: A place theory of sound localization (of barn owl). J. Comp. Physiol. Psychol. 41 [1948]: 35-39.
When the mouse rustles on the left, the right fibre "1" and the left fibre "7" will be excited. If it rustles on the right, the left fibre "1" and the right fibre "7" will be excited.
In contrast, if we look at pulse-shaped time functions (long pauses and needle-shaped pulses), we see that both signal forms opposite properties in the interference networks: A consideration of cross interference (two channel analogy: cross-correlation) shows properties of sinusoidal time functions in explaining cross interference (harmony, music, beat, sense of time), while pulse-shaped time functions have optimal properties for data addressing and signal transmission.
However, sinusoidal signals do not occur in a nerve network; we find these in acoustics (example Acoustic Camera.
The nerve equivalent is represented by more or less dense pulse trains, whose geometric pulse length and whose geometric pulse spacing (correspondence to the physical wavelength) varies. Geometric pulse spacing and geometric pulse lengths are the key parameters of interference networks: they determine almost all imaging qualities (for more see [6]).
2 First Neural Interference Circuits
Interferential data addressing works better, the less dense (sinusoidal) the time functions are. (Nerve impulses move at speeds in the range of µm/s... m/s, with typical impulse durations of 0.1 ms to 100 ms), find a Table in [8].
Konishi's circuit doesn't just work between different media. Let's assume that the space labeled 'sound space' also consists of neurons with connections to the 'relay stations'. The properties of the network would hardly change. Even then we would get a mirror-inverted excitation mapping. For this purpose, both neuronal fields only needed to be connected via more than two axons. This idea took shape (independently of Jeffress and Konishi) in 1992 and adorns the cover of the manuscript "Neural Interferences", Figure 3.
Fig.3: Animation of the cover image of the manuscript 'Neural Interferences' [6] (1993) - a monomedia interference circuit. This simplest interference circuit provides mirror-inverted, topical projections and images between the transmitting field S and the receiving field M. In principle, delay-affected interconnects are assumed in IN.
3 Why were the delays forgotten?
1943 End Before the Beginning: Birth of the ANN
Why was Jeffress [9] forgotten? The question of why such remarkable features were overlooked for fifty years leads the computer pioneers' path back to the 1943 paper [2] of McCulloch/Pitts.
To summarize the chapter in advance: The article by McCulloch/Pitts became the birthplace of digital circuit technology, (digital) algorithms, all programming languages and unfortunately, also of artificial neural networks (ANN). But delay times on nerves were replaced by states and clocks. With disastrous consequences for the beginning research on nerve networks.
With the work of John von Neumann, but also with that of Conrad Zuse, the fiction of the computer emerged in the early 1940s. Potentials became a preferred means of representing interconnections. Representing delaying interconnections requires much more computing effort than reducing an interconnection to a node. Leibniz's binary system (known a hundred years later as Boolean algebra) is abstracted from discrete and fixed values or states, omitting time functions. The invention of a "clock" made this possible.
But a clock represents a type of infinitely fast action at a zero distance that cannot exist in a nervous system! There, short impulses travel very slowly along (sometimes very long) nerve fibers.
Let's look at the following circuit. If we consider this as a normal digital circuit with states, clocks and the node abstraction of wires, then we see two gates A and B that are connected with the same nodes, whose signals are therefore processed in the same way.
If we consider it as a neural pulse circuit in which the geometric pulse length is shorter than the length of the connecting cables, an additional delay τ is created, whereby A and B (in the case that they are both AND-gates) are never activated at the same time. Gate B would become active and send a pulse to the output, while gate A would remain inactive.
Although neuron A and neuron B (AND types) may have an identical function, they do not respond in the same way to the same impulse assignments.
In the abstraction, however, this means:
Delays of interconnections dominate over weights.
However, if you model the same network with state sequences without path delays and time functions, the same network produces a wrong, completely different behavior. You think you are simulating a nerve network, but you are simulating something completely different.
Today we call these networks Artificial Neural Networks (ANN). From the very beginning, computer and ANN are thus bound to "states" - to discrete points in time (clocks) and to the abstraction of (delaying) pathways through nodes.
From then on, neuroscientists also used the node abstraction of nerve pathways that is common in electrical circuits - not realizing that the transit times (delays) of the pathways would be the decisive key to the computer science of nerve networks.
At the beginning of the 1950s it even became possible to show learning artificial neural networks (perceptron, backpropagation...) without delays on distributed runtime wires (nerves). Discretized time functions, node abstraction and clocks became popular.
As a result, Jeffress's model was probably forgotten. Only in the area of acoustic animal experiments can publications based on relative time be found in the following period, such as those by Konishi [1].
The genius of the computer pioneers in relation to the developing computer was to quantize Jeffress's interference circuit. A time function became a sequence of values, the delay became a discrete sequence of machine states. Delaying wires disappeared unnoticed from consideration. The state machine becomes the time-determining abstraction, not least thanks to the automaton theoretical foundations of Mealy [10], Moore or Medwedjev, the abstraction that creates the computer.
Strangely enough, in 1991 it was precisely the advanced microelectronics with hundreds of thousands of transistors that initiated a reconsideration. For a prestige object of a telecommunications manufacturer (16x16 ATM switching network with 154 MHz clock and 860,000 transistors), the author realized, that simultaneity can only be maintained in parts. The clock became faster than the propagation times of the signals on the chip.
The problem of all automaton is increasingly becoming the simultaneity that has to be achieved via the clock in the system under consideration (circuit, printed circuit board). This is exactly what is becoming increasingly difficult to achieve with ever larger circuits, higher clock frequencies, thinner interconnects and ever larger surface resistances (R□·L/W) of the clock lines.
"Simultaneity" only applies in some areas of fast and large circuits. There must be a decoupling between them (asynchronous couplings via latches, FIFOs, etc.). (It is still unclear whether nature took a comparable path of division between synchronous nuclei and interferential circuitry with known neuronal columns.)
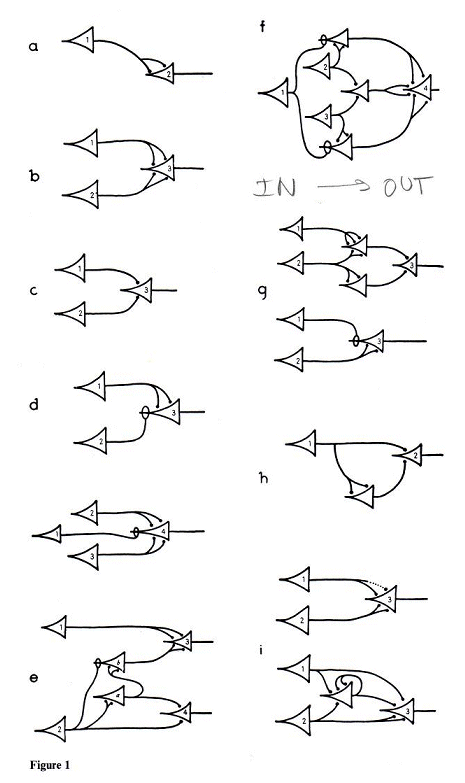
Fig.4: McCulloch-Pitt's representation, source [2]. Note that the flow of information goes against the direction of the arrow of the symbol, whereas today's logic inverter points with the tip in the direction of the signal.
While McCulloch/Pitts began their article [2] in 1943 with the sentence:
"The velocity along the axon varies directly with its diameter, from less than one meter per second in thin axons, which are usually short, to more than 150 meters per second in thick axons..."
they concentrate on the next page on state sequences. Among other things, the physical requirements already state:
"...
2. A certain fixed number of synapses must be excited within the period of latent addition in order to excite a neuron at any time, and this number is independent of previous activity and position on the neuron.
3. The only significant delay within the nervous system is synaptic delay.
..."
What didn't fit was made to fit. This abstraction has consequences. The continuous timeline is divided into states. At the end of the publication, terms will inevitably emerge that will characterize the new computer world, but which largely lose their reference to interference. Instead of an expression in the form of a time function:
f1(t) = f2(t-T1) + f3(t-T2) + ...
where T1 and T2 could represent floating delays caused by wire delays, in McCulloch/Pitts we only find expressions in form of clock numbers
N3(t) :=: .N1(t-1) .v .N2(t-3)
In the original essay of the neuronal era [2], a floating channel delay Tx is rounded to i (i as an integer state). The interference significance of small delays for location assignment (Jeffress) was unknown; floating point delay times are not given any informational significance.
With regard to historically following automaton networks, we can recognize successive automaton states in the discretization. But the idea of interference, superposition, and wave fields falls by the wayside. The meaning of a delay Tx (float) as an identification of the intrinsic, continuous delay of a nervous pathway is lost. Until 1993, delays remained uninteresting and remained in the shadow of state machines - far from any relationship to wave fields, projections or time functions. (We will discuss the chapter on "delay learning" which emerged in the early 1990s elsewhere).
A time function f(t-Ti) (t floating) is replaced by a sequence of states or values N(i), N(i+1), N( i+2) abstracted with integers i - automata theory and computers could emerge. Critics may note at this point, that a border crossing f(t) to N(i) is unproblematic for large i: that shouldn't be the case be contradicted, but historical development apparently also missed this opportunity.
(I apologize for the inhomogeneity of the notations. Notations from different disciplines and periods come together here, which couldn't be more contradictory: state machines - wave theory - optics. I always try to stay close to the original).
In the later, biology-related 'Adaline' neuron model by Widrow and Hoff [3], for example, there is no longer any reference, although state sequences and sketches of neural networks also appear here. The synapse was recognized - legitimately or not - as the carrier of weigths of neuronal information.
The fact that delays and waves could be just another form of expression of a sequence of automaton states only became apparent with the Thumb experiment [8] transparent. Even more modern works [4] that characterize this dilemma do not yet introduce time functions and waves. Neuroscience remained stuck in automata theory for decades.
Seen in this way, Jeffress's idea was a brief flash of thought in 1948 that was forgotten due to a lack of technological relevance.
On the other hand, the models of the Nobel Prize winners Hodgkin/Huxley (1952), which are very close to biology, could have shown a way to discover interferential projections by chance. Unfortunately, these models are so loaded with detail that even in 1993 only a few dozen neurons could be simulated at a time. The view of principle was eaten up by overwhelming detail.
In summary, the development of science up to the end of the last millennium can be characterized as follows:
- The quantization of time (since McCulloch/Pitts) changed the theory of neural systems so roughly that their research was completely blocked.
- The question of (synaptic) learning seemed to be completely solved by Artificial Neural Networks (ANN) - there was no need to deal with interference networks at all.
On the one hand (as my simulations showed) the temporal and spatial choice of the quantization intervals has consequences for the fundamental ability to achieve a (correct) projection. Interference images are so sensitive that changing a single parameter can immediately destroy the image.
On the other hand, a reference back to biology is only possible if there is sufficient structural equivalence. However, the actual structure of a nerve network can be better translated into delay sections than into sequences of states.
Thirdly, with the help of time functions, the physical properties that characterize runtimes develop in a self-running manner. So a branching of the interconnects, the ends of which are bent towards each other, already creates a (Huygenian) double slit pattern as an interference mapping along the contradirectional interconnects (Try to realize a double slit pattern in an automaton model in a physically correct way (i.e. in space and time). It turns out that that the fineness of the time and spatial resolution determines whether simulations can be expected to produce meaningful results. The fatal effects of incorrectly discretized spatial and temporal structure on the wave field can be seen here, for example [12] study). Unnatural square waves can be seen.
In contrast to other works, the studies presented here were based on time functions whose delay Tx integrates the distance traveled. Consequently, there is no conduction potential, only (continuous) potentials and time functions of discrete conductor path locations (points) exist. If a time function travels through space, its dt is integrated according to the valid master speed v and the path element ds passed through
dt = ds/v
Accordingly, spherical waves inevitably arise as realistic propagation models of a wave front, even if these represent a poor idealization of the (severely inhomogeneous) nerve network. Realistically, one should imagine discrete (one-dimensional) waves on networks.
Topology-preserving maps and mirror-inverted projections are known from the nervous system. We know of mirror-inverted 'projections' without being able to name their causes; think of this, for example Homunculus. (Note: The concept of projection is also used analogously in other specialist areas. But here is only the (optical), mirror-inverted image of waves and their Interference integrals meant).
Investigations with pulse-propagating networks have now shown that, comparable to the mirror-inverted image that an optical space provides, for example, images in stochastically connected networks can be simulated through very precise modeling with wavefronts.
The consequences are stated: If biological systems were actually interference systems, only relatively working, interferential measuring devices would be able to get interferential reconstructions from these systems.
With PSI-tools, a measuring system was developed in the 90s that could have obtained information from a parallel runtime period and processed it interferentially. Unfortunately, the time was only ripe for the acoustic camera. At that time, multi-channel recordings from nerves could only be obtained in unusable qualities.
If fortunate circumstances are encountered, it should be possible to reconstruct the first 'images of thoughts' using PSI-like tools. You certainly shouldn't imagine using it to accurately decipher dreams. Rather, it seems realistic to assume that we find multiply distorted, interwoven runtime spaces whose mappings appear to be holomorphic in nature.
5 What characterizes an interference circuit?
The interference character of the Jeffress model reveals, that the means available to us with Leibniz's (Boolean, binary) algebra to determine an informational task of a nerve network are not sufficient.
In a stochastically connected, pulse-propagating network, signal processing can only take place where several pulses meet. Logical processing therefore appears located in interference networks (IN).
This means: Neighboring locations form different connections and different outputs with identical functions. Or: The limits of neurosurgery have been reached if an operation significantly changes the relative transit times of the fibers.
The problem becomes clear using the example of a collision between two cars at an intersection: a crash only occurs if both cars are in the same place in the same thousandth of a second. If we use discretized time (for example to one minute), certain crashes would not be possible. But false, completely artificial ones would emerge.
Note: A too coarse quantization of time or location completely changes the function of interference networks!
6 Simulator and measuring device
Since interference networks cannot be calculated very well with a sharp pencil, a special simulator was developed in 1993 called Bio-Interface, later renamed in PSI tools. This made it possible to parametrically simulate the simplest interference circuits, whereby the neurons in the generator and detector field can be arranged, for example, as bitmaps of a defined resolution. PSI stands for 'Parallel and Serial Interference', which meant that the simplest projections and reconstructions could be calculated. In particular, the world's first acoustic images and films were created in this years.
Functions
Resulting excitation maps can be calculated in two ways: as interference integrals or as time-resolved wave fields (interference movies). With an otherwise identical algorithm, interference integrals are calculated in relation to pixels, while I.-movies are calculated in relation to time steps.
Each channel source and sink point can be freely selected in the space. Channel data can be easily changed, duplicated or summed in this way. The generator field and detector field are designed as bitmaps, the origin and physical size of which can be freely selected regardless of channel sources. Matrix grid, origin, speed and physical field dimensions can each be freely selected. The timing of time functions can be specified as a sequence of values in the channel data synthesis. Refractoriness, time functions and pulse distance can be specified.
7 Reconstruction versus projection
Every interferential projection potentially consists of three parts: On the one hand, the reconstruction of the source locations of the generator space is interesting for technical applications (Acoustic Cameras), Figure 6 (top). On the other hand, the calculation of projections is of interest, Figure 6 (bottom) in any differently designed detector spaces, e.g. for the calculation of neuronal projections. Last but not least, there is the real excitation map as the origin of the channel data (not shown).
Projection and reconstruction are intimately linked. If we run PSI tools in the standard form with inverse delays, a laterally correct interference integral (reconstruction) is created. If we use non-inverted time by inverting the time axis, a mirror-image interference integral (projection) occurs; assuming we choose identical location coordinates.
In PSI tools there is therefore a function for reversing the time functions of the channels: In the standard case, a reconstruction is calculated with an inverse running time axis (negative delays) and with the parameters of the detector space. If the time axis of the channels is also reversed, a non-time-inverted but mirror-inverted projection is created.
Properties
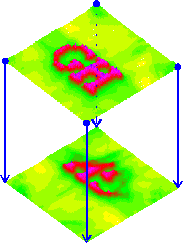
Fig.5: Reconstruction (top) and projection (bottom) of an excitation map as an interference integral from the same, previously synthesized time functions of the channels (channel data), PSI Tools 1994-1996.
All channels have the same delay time, the propagation speed is the same in both fields. The image symbolically expands the Konishi model to four channels. It represents an interferential mapping that answers both questions: Given four time functions (blue). We see the reconstruction of the generator space above and the projection into the detector space below. The reconstruction is used to determine the template (top) and the projection is used to calculate the image (bottom).
Imaging conditions can already be guessed here:
1) the geometric pulse length (length of the pulse wave) must be small compared to the object size to be resolved;
2) Assuming low channel numbers, the time interval (refractoriness) between two pulses must be larger as the field size. Measures of time and length are connected via media velocity (v = s/t).
In addition to imaging elements, channel data can also carry noise amplitudes. The result of an interference analysis is unavoidable both imaging and spectral components. Consequently, sequential coding (phonetic images) can be calculated, as can projections and images. As with optics, the two components cannot in principle be separated from each other.
The temporal component manifests itself when pulses are applied to the field too quickly one after the other, for example because the refractory period (the recovery time) of the transmitting axons is too short. Then additional interference of a wave occurs with preceding and following (other) waves, correspondingly resulting in an aliasing pattern in the interference integral.
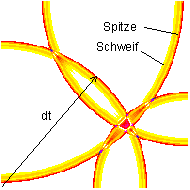

Fig.6: 4-channel wave field of a projection (PSI-Tools, 1995)
The image shows a projection of a four-channel transmitted scene onto a receiving field. The feed points are at the corners of the field. The time shortly after a quadruple interference is shown. See also these simulations. It becomes clear that maximum excitement can only arise at exactly the place where many waves meet at the same time. Temporal relativity of waves then encodes the function of the network.
To return to the title question: If we view time functions (waves) running through space and delays distributed on channels (nerves) as physical realities, then any IT function in intimately interwoven nerve networks is only conceivable in interference circuits (think also of redundancy): Consequently there are not only images of thoughts, but almost all conceivable processing variants in the nerve network are tied to projections (of an optical type) - i.e. to mirror-image-like maps: Consequently, there are only images of thoughts as universal Communication principle of the nervous system. It makes sense to assume that a motivated neuroresearcher will soon be able to prove it.
Interference networks therefore deal with properties between waves that coincide relatively in time and their interference integrals (colloquially: with images from interfering time functions).
[1] Konishi, M.: The sound location of the barn owl. Spectrum of Science, June 1993, p. 58 ff.
[2] McCulloch, W.S.; Pitts, W.: A logical calculus of the ideas immanent in nervous activity. 1943 Bulletin of Mathematical Biophysics 5: 115-133; p.18 ff. in [13]
[3] Widrow, B., Hoff, M.E.: Adaptive switching circuits. 1960 IRE WESCON Convention Record, New York: IRE, p. 96-104; p.126 ff. in [13]
[4] Rumelhart, D.E., McClelland, J.L.: A Distributed Model of Human Learning and Memory. in: Parallel Distributed Processing. Bradford/MIT Press Cambridge, Massachusetts, vol. 2, eighth printing 1988.
[5] Hodgkin, A.L., Huxley, A.F.: A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. Journ. Physiology, London, 117 (1952) p. 500-544
[6] Heinz, G., Neural Interferences. Working manuscript, 300 pages, 1993
[7] Heinz, G.: Modeling Inherent Communication Principles of Biological Pulse Networks. SAMS 1994, vol.15, no.1, Gordon & Breach Science Publ. UK
[8] Heinz, G.: Relativity of electrical impulse propagation as a key to the computer science of biological systems. 39th International Scientific Colloquium at the TU Ilmenau September 27-30, 1994, Volume 2, p. 238-245
[9] Jeffress, L.A.: A place theory of sound localization. Journ. Comparative Physiol. Psychol., 41, (1948), p.35-39
[10] Mealy, G.H.: A Method for Synthesizing Sequential Circuits. Bell System Tech. J. 34, Sept. 1955, p. 1045-1079
[11] Shannon, C.E.: A Mathematical Theory of Communication. Bell System Technical Journal. Short Hills N.J. 27/1948, p. 379-423, 623-656
[12] Alain Destexhe, Diego Contreras, Terrence J. Sejnowski and Mircea Steriade: A model of spindle rhythmicity in the isolated thalamic reticular nucleus. Journal of Neurophysiology 72: 803-818, 1994; for the fatal effect of discretized time see (PDF), specifically: (MPG)
[13] Neurocomputing - Foundations of Research. Edited by J.A. Anderson and E. Rosenfeld. The MIT Press, Cambridge MA; London UK, 1988, 729p.
"Wherever something great has been achieved on the anvil of technology, hammer blows were necessary. Resistance had to be broken down, contemporary opinions had to be hammered together so that the new form could grow out with indomitable creative power..."
Carl Friedrich Benz
"Wherever a dangerous new theory emerges,
she is fought to the death.
Therefore, distrust praise
and do not be annoyed by ignorance."
Manfred Frankenfeld
Basics: historic/pressinf/bilder_d.htm
Features at a glance, movies: historic/index.htm#neuro
Publications:
publications/index.htm
PS
Publishing essays on IN was initially hardly possible. The theory of IN could not be taught, which is probably why it remained so unknown to this day. It was only the application of the IN as an acoustic camera that aroused media interest, see press pages. This is also why many of the original articles on IN can only be found on the Internet.
gh 2020
Page URL: historic/intro/intro_e.htm
Upload of the german site Sept. 30, 1995; edited several times
Mit Google https://translate.google.com aus dem Deutschen übersetzt. Mit manuellen Korrekturen (24. Januar 2024)
Visitors since Dec. 2021: