"Wenn Theorie auf Erfahrung warten sollte, käme sie nie zustande."
Friedrich von Hardenberg
(Anmerkung: Die Seite zeigte ursprünglich Ausschnitte von Kapitel 12 "Biologienahe Modellierungen" des Buches "Neuronale Interferenzen" von 1993 [NI93]. Zu einigen hier gezeigten Bildern existieren auch Animationen)
1. Vorwort
2. Daumenexperiment
3. Dermatom
4. Delay-Masken
4.1 Projektion in Selbstinterferenz
4.2 Codegenerierung
4.3 Codedetektion
4.4 Datenadressierung
4.5 Nachbarschaftsinhibition
4.6 Pegelgenerierung
4.7 Zusammengefaßt
5. Pulsfolgen (Bursts)
6. Entfernungsbestimmung mittels Echo
7. Ortung eines Geräusches
8. Penfields 'Homunculus'
9. Ausbalancieren eines menschlichen Skeletts
10. Das visuelle Systems (chiasma opticum)
10.1 Unser Weltmodell
11. Erkrankungen des Nervensystems
12. Sensibilität der Hand
13. Wie ein Regenwurm schlängelt
13.1 Strickleiter in einem Hauptstrang
13.2 Beinsteuerung von Insekten
14. Ein hörendes Neuron
Die hier als Interferenznetzwerke dargestellten Schaltungen sind keine elektrischen Netzwerke, sondern nervliche Netzwerke mit extrem geringen Leitgeschwindigkeiten. Alle Leitbahnen sind Laufzeitleitungen! Die elektrische Knotenabstraktion einer Leitung gilt hier nicht.
Im Nervensystem wimmelt es von spiegelverkehrten Abbildungen. Haben diese vielleicht eine Ursache?
Denkt man über Projektionen in zeitverzögernden Netzwerken nach, so wird einem schnell klar, daß vorwärtslaufende Zeit (ohne Tricks) nur spiegelverkehrte Abbildungen liefern kann. Der Blick in einige Neuroanatomie-Lehrbücher zeigte dem Autor 1992, daß es im Nervensystem nur so von spiegelverkehrten Karten wimmelt.
Das war die Motivation, 1992 das Daumenexperiment zu machen und gleich darauf 1993 das Buch Neuronale Interferenzen innerhalb weniger Monate zu schreiben.
Eine wichtige Frage der Erkennbarkeit des Nervensystems ist die nach dessen Vernetzung. Wie stellen wir uns eine Verbindung zwischen miteinander kommunizierenden Einheiten vor? Als direkte Verbindung wie eine Leitung, die Klingelknopf und Klingel verbindet ("Klingeldrahtmodell")?
Reduzieren wir diesen Gedanken, hieße das, jedes Neuron müsste potentiell in einem universell lernenden Nervennetz mit jedem anderen Neuron (von einigen Milliarden) eine Verbindung eingehen können. Wenn demzufolge angenommen werden muß, daß potentiell jedes Neuron mit jedem kommunikationsfähig sein muß, heißt das, jedes Neuron ist mit jedem zu verbinden.
Dies wiederum hätte zur Konsequenz, daß es in allen 100 Milliarden Neuronen klingelt, wenn auf einen Klingelknopf (erregtes Neuron) gedrückt wird. Mit Klingeldrahtmodellen jeglicher Art läßt sich das Gehirn folglich nicht beschreiben.
Wie aber dann?
Die neuronale Netzwerktheorie brachte seit den 40er Jahren einen neuen Ansatz hervor. Aus der Schwellwerttheorie ("Threshold Logic", Jan Lukasiewicz 1920, 1922) entstand die Idee, Neuronen nur zu (verbinden oder) zu erregen, wenn ein Schwellwert überschritten wird, der vom gleichzeitigen Feuer verschiedener Neuronen stammt.
Damit ließen sich zumindest kleine, homogene, getaktete Netzwerke beschreiben.
Die Grenzen dieser Modelle aber werden erreicht, wenn Code- oder Geräuschverarbeitung gefragt ist, oder wenn Signale durch Kanäle laufen (chiasma opticum, homunculus).
Beziehen wir Ortskoordinaten und Verzögerungszeiten auf allen Pfaden mit in ein Modell ein, sind wir bei den Interferenznetzwerken. Wie aber soll Kommunikation geschehen? Natürlich über Interferenzintegrale, über relative Gleichzeitigkeit des Eintreffens von Pulsen. Relativ soll heißen, daß es gleichgültig ist, wann ein Puls irgendwo startete. Wichtig ist nur, daß er mit seinen Zwillingsbrüdern zusammen zeitgleich an einem Ziel ankommt. Dabei ist das Ziel ungewiß: es ist einzig durch die Gleichzeitigkeit definiert!
Das Eisenbahnnetz eignet sich als Denkmodell. Bahnhöfe stehen für Neuronen, Strecken für Leitbahnen, Züge für Pulse. Mögen am Berliner Hauptbahnhof Züge aus Frankfurt/Oder, Magdeburg, Rostock, Leipzig und Dresden ankommen. Damit Passagiere zwischen allen Zügen umsteigen können, wäre erforderlich, sie in Berlin exakt gleichzeitig ankommen zu lassen. Damit aber Züge in Berlin gleichzeitig ankommen können, müssen sie in den Ausgangsorten zu verschiedener Zeit losfahren, wenn wir voraussetzen, daß sie im allgemeinen unterschiedliche Fahrwege und Fahrzeiten haben.
Orte hoher Interferenz (lokale Überlagerung vieler Wellenberge) bedingen ein sehr genaues, raum-zeitliches Timing der beteiligten Elementarwellen. Diese können von überall her kommen. Die Wellenberge müssen lediglich genau am Zielort gleichzeitig ankommen und aufeinander treffen. Wir begreifen plötzlich ein Nervennetz als die brillanteste, dezentrale Maschine des Universums. Auch begreifen wir, daß Interferenznetzwerke eine Gruppe komplizierter Netzwerke sind, die die Eigenschaft haben, gleich mehreren sendenden Neuronen entsprechende empfangende Neuronen zuzuordnen. Und wir begreifen, daß wir in deren Erkenntnis noch vollkommen am Anfang stehen. Netzwerke, die dies leisten, wollen wir projizierende oder Interferenznetze nennen.
Der Autor hatte das Glück, einige von ihnen zu entdecken.
Nachdem mir 1992 klar wurde, daß Nerven sehr langsam leiten sollen und daß wohl Pulse Träger der Information sein müssen, war meine erste Frage die nach der Leitfähigkeit biologischen Materials.
Eines der ersten Experimente war es, ein Kotelett auf elektrisch/ionische Leitfähigkeit zu untersuchen. Eine Leitgeschwindigkeit konnte nicht ermittelt werden, dafür war das verfügbare Röhrenoszilloskop zu langsam. Das Kotellett verhielt sich wie eine RC-Ersatzschaltung.
Ich besorgte mir Bücher zur Neuroanatomie. Einerseits fand ich die Tabelle zu Leitgeschwindigkeiten nach Erlanger/Gasser, andererseits lernte ich Herrn Dr. Torsten Griepentrog kennen. Gemeinsam entwickelten wir das Daumenexperiment.
Sollten Sie sich wundern, daß es so schwierig ist, nervliche Daten zu bekommen, so bedenke man, daß die ionische Leitung des Fleisches um ein vielfaches besser und schneller ist, als die der darunter verborgenen hauchdünnen Nervenfasern. Ohne den Abschirmring unterhalb der Daumenelektrode ginge gar nichts, siehe Fotos der Meßnordnung in Abb.7 von IWK94.
In der Tat: Nerven sind von der Evolution nicht dazu geschaffen worden, schnell zu leiten. Im Gegenteil: Sie leiten extrem langsam, verglichen mit dem sie umgebenden Material!
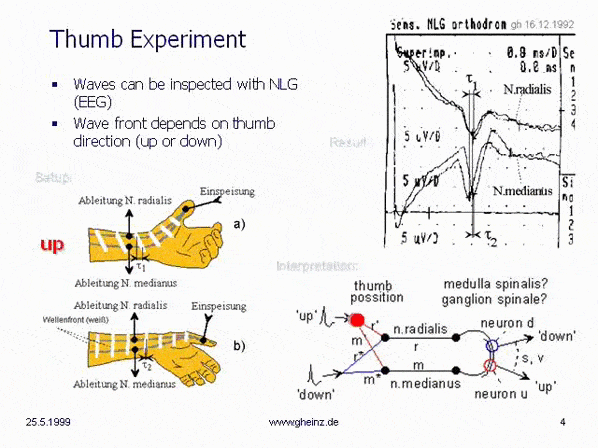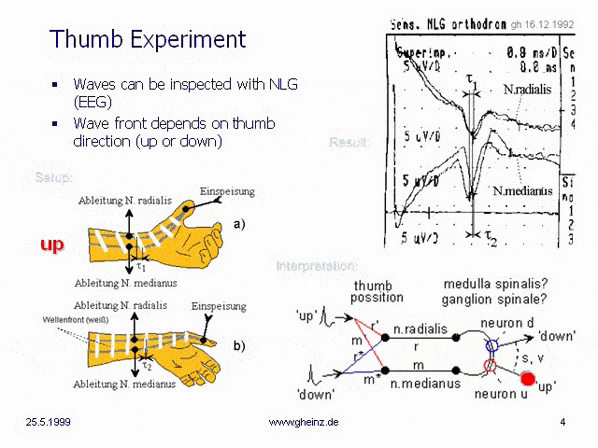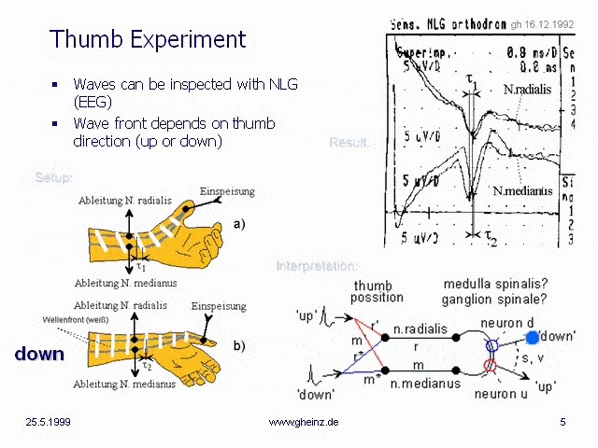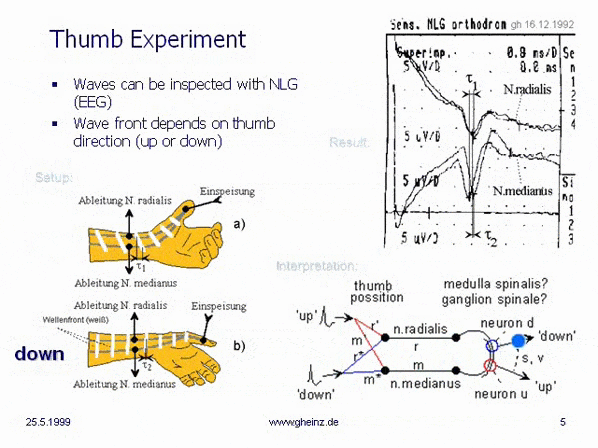
Wird der Daumen elektrisch stimuliert, so läßt sich an zwei nichtinvasiv zugänglichen Nervenbahnen (N. radialis und N. medianus) der fortschreitende Impuls abgreifen. Der EEG-Averager ist auf mindestens 10-fach einzustellen, eine Schirmelektrode ist zwischen Stimulus- und Sensorelektroden anzuordnen, um Artefakte zu vermeiden.
Eine bloße Lageveränderung des Daumens sorgt dafür, daß die Zeitdifferenz des Eintreffens beider Impuls-Teile um etwa 0,5 Millisekunden variiert. Die Wellenfront des Impulses passiert mehr oder weniger schräg die Sensorelektroden. Im Bild ist sogar eine Vorzeichenumkehr der Wellenfront bei nach innen gerichtetem Daumen zu beobachten. Im rechten Bildteil sind mit der Daumenstellung variierende Kartierungen auf einem hypothetischen Empfangsfeld dargestellt.

Bild 1: Daumenexperiment, G.Heinz 1992, Quelle. Es war das Einführungsexperiment des Autors, gemessen mit einem Elektroenzephalographen (EEG).
Ein Einführungsexperiment des Autors, gemessen mit einem Elektroenzephalographiegerät (EEG). Die Stimulation des Daumens durch Ringelektroden und die Aufzeichnung zweier Nerven (n.radialis und n.medianus) zeigt die Entstehung von Partialimpulsen in Abhängigkeit von der Stellung des Daumens. Zwischen dem Daumen und Sensorelektroden ist eine abschirmende Elektrode (Ring) zu setzen, um Artefakte zu vermeiden. Einstellung für den Averager: Mittelwertbildung mindestens 10-fach.
Man erkennt am EEG, daß die sofort einsetzende elektrisch/ionische Leitung trotz Abschirmring um ein Vielfaches stärker ist, als die abgenommenen Signale von n.radialis und n.medianus. Man erhält nur mit Averager ein verwertbares Signal.
Wie wir bei der Diskussion des Hebbschen Lernens noch sehen werden, ist anzunehmen, daß die winzig kleinen, von Axonen ausgesandten elektrischen Felder offenbar den Ausgangspunkt darstellen, damit Hebbs Rule auch funktionieren kann und ein dendritischer Wachstumsprozeß einsetzt.
Wird die Daumenposition verändert, ändert sich die Verzögerungsdifferenz zwischen den Sensorelektroden. Die Wellenfront verläuft mehr oder weniger diagonal an den Sensorelektroden. Wenn wir annehmen, daß an anderer Stelle (Medulla spinalis, Ganglion spinalis...) Neuronen in einem realen Abstand (s) im Schaltkreis liegen, können wir die Eigenschaften dieses Interferenzkreises mit realen Geschwindigkeiten berechnen. Die Nervenleitung kann recht schnell sein, allerdings nur auf den myelinisierten Übertragungsadern (r, m).
Nehmen wir an, daß es an einem anderen Ort (Medulla spinalis?) einen gegenläufigen Interferenzkreis (siehe Abbildung) gibt, dann können dort in Abhängigkeit von der Daumenstellung um einen Abstand s voneinander entfernte, verschiedene Neuronen erregt werden (Neuron x bzw. Neuron y).
Dieser einfache Interferenzkreis zeigt bereits eine gespiegelte Projektion (Rot zu Rot, Blau zu Blau) (Messung vom 16.12.1992, Landesklinik Teupitz; Dr. Gerd Heinz bei Dr. Torsten Griepentrog). Weihnachten 1992 wurde das schlafloseste Fest meines Lebens. Jetzt mussten die Gedanken "nur noch" sortiert und niedergeschrieben werden. Das Buch "Neuronale Interferenzen" wurde im Kern innerhalb von 3 Monaten niedergeschrieben.
Die erste Veröffentlichung des Daumenexperiments erfolgte im IWK-Aufsatz "Relativität elektrischer Impulsausbreitung als Schlüssel zur Informatik biologischer Systeme". 39.IWK Ilmenau (PDF, deutsch), (HTML, deutsch) Übersetzung (HTML, Englisch).
Weitere Details finden Sie in der Web-Publikation "Beobachtbare Relativität neuronaler Impulsausbreitung - Ein Versuch mit Konsequenzen für die Neuroinformatik" (PDF deutsch).
3. Interferenzkreis - Dermatom - somatotopische Abbildung - Projektionsbahnen

Bild 2: Kommunikationsprinzip eines Interferenznetzwerks nervlicher Art
Diesen einfachsten, monomedialen Interferenzkreis zeigte 1993 das Titelbild des Manuskripts Neuronale Interferenzen. Ein sendender Raum interferiere über Axonen A und A' mit einem Empfangsraum. Neuron P möge einen Puls in das Netzwerk senden. An der Stelle P', an der beide Pulse gleichzeitig ankommen, entsteht ein überdurchschnittlich hoher Wert des Interferenzintegrals, dort ist Gleichzeitigkeit vorhanden und nur dort entsteht neue Erregung. Vergleichbar zu einer optischen Linsenprojektion entsteht ein spiegelverkehrtes Bild vom sendendem Raum im Empfangsraum - eine Projektion optischer Art entsteht.
Stellt man sich die Räume größer vor, so wäre erkennbar, daß die Zeichnung für sämtliche ausfächernden Projektionsbahnen des Nervensystems - auf- wie absteigende stehen kann.
Bemerkenswert ist, daß Erregung vom Ort P an einen Ort P' immer nur spiegelbildlich weitergegeben werden kann - aus einer Bildvorlage P wird ein spiegelverkehrtes Abbild P' - wie in der Optik. An der Animation (hinter dem Bild) wird klar, daß Sende- und Empfangsorte im Interferenzmodell einzig und allein über Laufzeiteigenschaften (delays) des verbindenden Netzwerkes definiert sind - nicht aber über die Art und Weise der Verkabelung. Eine Kreuzung ist beim Sehnerv ebensowenig erforderlich wie in der Pyramidenbahn. Sie können vorhanden sein, haben aber kaum Einfluß auf die Art entstehender Abbildungen.
Eine Besonderheit aller Interferenzabbildungen besteht in deren zusammenhängender (reißfester) Projektion, siehe z.B. eine Simulation überlagerter Interferenzkarten in nervlicher Parametrisierung. Aus dem Nervensystem sind ausschließlich spiegelnde, somatotopische Abbildungen dieser Art bekannt. Vom Dermatom ist der sog. Fasertausch bekannt: Ein Dermatom wird stets von mehreren Nerven innerviert. Selbst das autonome Gebiet ist nicht autonom. Es zeigt mindestens in einer Richtung eine Überlagerung verschiedener Nervenfasern. All dies sind ganz klare Indizien für die Funktion des Nervensystems als Interferenznetzwerk: Das Nervennetz ist nur interferenziell begreifbar und berechenbar.
4. Delay-Maske und dynamische Elementarfunktionen eines Neurons
Akzeptieren wir die reale Existenz niedriger Leitgeschwindigkeiten, endlicher Laufzeiten und geometrisch (λ = v·t) kurzer Pulsnadeln in Nervennetzen und akzeptieren wir mehrfach parallele Übertragungsmöglichkeit von Pulsen, dann haben wir auch anzuerkennen, daß Kommunikation zwischen zwei Neuronen umso effizienter wird, je gleichzeitiger und präziser ankommende Partialwellen aufeinander treffen (miteinander interferieren).
Selektivität eines Neurons hat dabei etwas mit einer äußerst penibel abgestimmten Laufzeit-Architektur zu tun:
Damit Hebb'sche Gewichte überhaupt erlernbar sind, müssen die Delays stimmen, muß ein sauber abgestimmter Interferenzkreis existieren, damit das betreffende Neuron überhaupt adressiert werden kann.
Über die Dicke und Länge einer Faser ist z.B. ein Teil-Delay auf maximale Erregung des Neurons abstimmbar.
Wie aber können wir diese Dinge mathematisch fassen?
Betrachten wir dazu ein elementarstes Verknüpfungsnetzwerk bestehend aus zwei Neuronen sowie einigen verzögernden Fasern. Zunächst wollen wir einen simplen Puls mit maximaler Effiziens zwischen beiden Neuronen transportieren.
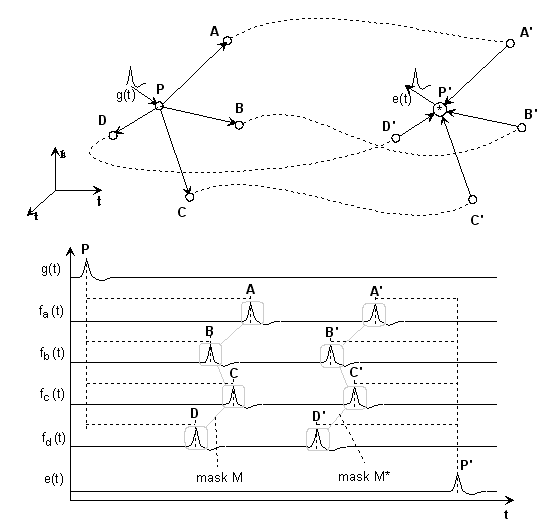
Bild 3: Einfachster, nervlicher Interferenzkreis
Wir spalten das Gebilde in drei Teile auf:
Die Delays PA...PD sollen einem Puls- generierenden Neuron zugeordnet sein, diese Delays nennen wir in Matrixdarstellung Delayvektor oder Maske
M = {PA,PB,PC,PD}.Delays AA'...DD' sollen den Übertragungsweg mit einem Delayvektor
L= {AA',BB',CC',DD'} darstellen;Delays A'P'...D'P' sollen zum empfangenden Neuron mit der Maske
M'= {A'P',B'P',C'P',D'P'} gehören, siehe Bild.Natürlich vergeht von P nach P' eine gewisse Zeit τ = {PP'};
in Vektornotation T = τ · {1} ({1} ist die Einheitsmatrix).
Multiplizieren wir z.B. die Zeitfunktionen in P' Sample für Sample miteinander (Faltung), dann wird schnell klar, daß die Laufzeiten der einzelnen Pfade identisch groß sein müssen, wenn wir keine Zeitfunktion aus Nullen erhalten möchten, falls eine der Zeitfunktionen Null wird:
(1) PA + AA' + A'P' = PB + BB' + B'P' = ... = PD + DD' + D'P'
in Vektornotation gilt dann:
(2) M + L + M' = T (Abbildungsbedingung)
Folglich hängen die drei Masken mathematisch zusammen.
4.1 Projektion in Selbstinterferenz
Das empfangende Neuron erhält die eingangsseitige Zeitfunktion nur dann identisch am Ausgang, wenn dessen Delaymaske die Bedingung aus (2) erfüllt
(3) M' = T - M - L
Neuron P' wird nur dann von P erregt, wenn es eine geeignete Delaymaske M' ausgebildet hat.
Erfüllt die Maske M nicht Bedingung (3), gilt also die Ungleichung
(4) M' ≠ T - M - L
und setzen wir additive Verknüpfung bei geeignetem Schwellwert in OR-Form voraus, erzeugt ein einzelner Puls am Eingang eine Pulsfolge am Ausgang. Neurologen nennen solche kurzen Pulsfolgen auch Bursts.
Wird das Bias sehr hoch gewählt (multiplikativer AND-Typ), so reagiert die Schaltung nicht auf Einzelimpulse. Statt dessen detektiert sie eine Impulsgruppe mit der Delaymaske M', siehe Bursts.
Finden wir Nervenzellen, deren Verzögerungsvektoren dem Zusammenhang
(5) M + L + M' = T
mit T = τ · {1}
({1} ist die Einheitsmatrix)
genügen, so sendet die eine einen Burst y(t) aus, den nur die andere empfangen kann, und den sie zu einem Einzelimpuls z(t) zurückverwandelt. Senden mehrere Nervenzellen, die unterschiedliche Verzögerungsvektoren besitzen, auf eine gemeinsame Übertragungsleitung, und existieren auf der Empfangsseite Nervenzellen, deren jede nur einen spezifischen Burst selektieren kann, so finden wir ein Übertragungsprinzip, daß die Übertragung verschiedener Datenströme auf einer gemeinsamen Leitung erklären kann. Dieses Prinzip soll 'Datenadressierung' genannt werden. Im Moment ist dieses Prinzip rein hypothetisch. Da es aber vergleichbar einfach (mit nur einer Elektrode) nachgewiesen werden kann, können wir hoffen.
Siehe speziell zur Nachbarschaftshemmung auch eine ausführlichere Darstellung in Kap.18 der "Zweiten Informatik".
Dasselbe Prinzip verhindert nun ein Überspringen von Erregung zwischen benachbarten Neuronen. Besitzen inkremental sehr eng benachbarte Neuronen Verbindungsstellen sowie identische Struktur, so besitzen sie etwa denselben Verzögerungsvektor M.
Da für eine Adressierung aber M + 0 + M' = T erfüllt sein muß (L = 0 verschwindet) und folglich M' = T - M gilt, die geometrische Struktur allerdings M' = M fordert, gibt es für M und M' nur die Triviallösungen Null und
(6) M' = M = T/2 = τ/2 {1},
die in gröbster Näherung bedeutet, daß die Koppelsynapsen beider Neurone kreisförmig im Radius r = v τ/2 um das Soma herum angeordnet sein müssen (Leitgeschwindigkeit v). Wir nehmen dazu an, die Soma der Neuronen befinden sich eng beeinander.
Somit erklärt dieses Prinzip auf Grundlage von Delays, unabhängig von z.B. inhibitorisch wirkenden Synapsenstärken, eine dynamisch wirkende Nachbarschaftsinhibition. Man könnte auch sagen, die Erregung springt von ihrer dynamischen Natur aus nicht zwischen zwei an gleiche Ortsknoten zusammengeschlossenen Neuronen über - was eine äußerst vorteilhafte Eigenschaft von Nervennetzen zu sein scheint.
Dieses Prinzip verhindert letztlich ein ungewolltes Überspringen von Erregung zwischen benachbarten Neuronen und den totalen Zusammenbruch aller Informationsübertragung.
Um Kontrollpotentiale für Bias o.ä. zu erzeugen, benötigen wir eine Möglichkeit zur Pegelgenerierung. Besitzt das detektierende Neuron eine integrierende Eigenschaft, so kann ein detektierter Burst zu einer Potentialanhebung führen. Wir nennen diese Eigenschaft Pegelgenerierung. Ist die integrierende Wirkung stark genug, so können auf diese Weise gleitende Hintergrundpotentiale geschaffen werden, die ihrerseits wieder benötigt werden, um Zooming- oder Movement zu steuern. Es ist anzunehmen, wir messen genau diese Steuerpotentiale im EEG. Eigene EEG-Experimente (siehe dort) erbrachten unzureichende, interferenzielle Rekonstruierbarkeit, dies würde dazu passen.
Siehe auch Kap.8b, S.191 und Kap.10, S.212 in NI93. Pegelgenerierung konnte in der Simulation verifiziert werden mit dem Simulator 'Neuronet' an der FHTW Berlin am 20.10.1994 (Peter Puschmann, Gunnar Schoel, Gerd Heinz), siehe VirEx96, 17. Experiment, S.17.
Es ergeben sich Gesetze, die in gewisser Weise als eine Erweiterung von McCulloch/Pitts um Hebb's rule und Jeffress Interferenzkreis aufzufassen sind.
Als dynamisch wirkende, neuronale Elementarfunktionen können wir am elementaren Interferenzkreis beobachten:
Codegenerierung Codedetektion Datenadressierung Nachbarschaftsinhibition Pegelgewinnung
Einige Eigenschaften wurden erstmals im Manuskript [NI93] erörtert. Aufbauend darauf lasssen sich komplexe Eigenschaften von Interferenznetzen erkunden. Die wesentlichsten sind:
Zooming einer Abbildung bei Veränderung der Ausbreitungsgeschwindigkeit Movement (Weglaufen) des Bildes bei ungleichsinniger Verzögerungsveränderung in den Übertragungskanälen Konjugation; verschmelzende Überlagerung von Abbildungen in einem Detektorfeld Interferenzüberlauf bei starker Befeuerung oder zu kurzer Refrakterität der Axonen.
Dem nicht sensibilisierten Beobachter mögen Pulsfolgen als stochastische Dichtecodierungen erscheinen. Indes deuten Codegenerierung und Codedetektion an, daß sie deterministisch eine Information codieren. Ein Burst M wird nur gehört vom dem Neuron, welches die passende Empfangsmaske M' besitzt. Damit kann eine einzige Leitbahn verschiedene Informationskanäle ("Klingelleitungen") tragen, siehe Bild 5c).
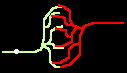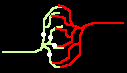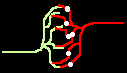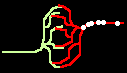
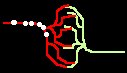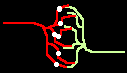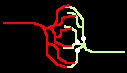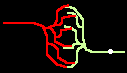
Bild 4: Codegenerierung und Codedetektion an zwei gekoppelten Neuronen. Ein ankommender Einzelimpuls (links) erzeugt mit der Maske M einen Burst (mittig), dieser wird nur durch die zu M inverse Maske M' = T - M in einen Einzelimpuls zurückgewandelt (rechts).
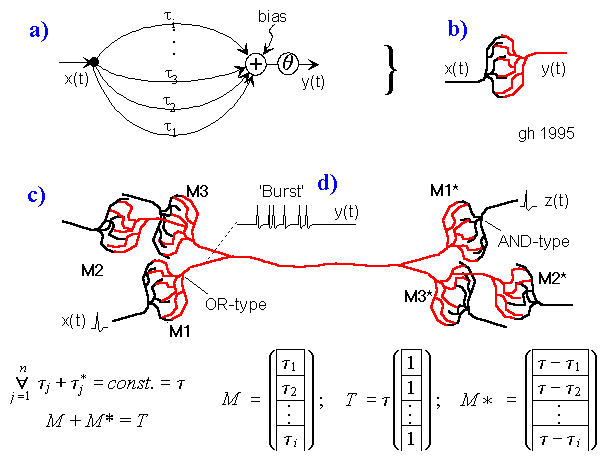
Bild 5: a) Ersatzschaltung einer Koppelstelle b) zweier Neuronen; c) Beispielverschaltung mehrerer Neuronen; d) erzeugter Burst.
Zur Funktion: Die Neuronen 1 bis 3 mögen verschiedene Masken (Verzögerungsvektoren) M1 bis M3 besitzen. Dazu mögen paarweise inverse Vektoren M1* bis M3* existieren. Dann springt (abgesehen von nicht betrachteten, möglichen Permutationen) die Erregung i.a. nur von M1 auf M1*, von M2 auf M2* und von M3 auf M3* über und visa versa.
Über die synaptische, neuronale Kopplung hinausgehend, die Gegenstand des Neurocomputing ist, spielen zeitliche Relationen bei pulsartiger Signalausbreitung im Nervensystem eine entscheidende Rolle. Die Gleichzeitigkeit des Ankommens von Impulsen entscheidet die Erregbarkeit eines Neurons.
Wir entdecken, daß nur durch die Beachtung von Verzögerungszeiten neue, neuronale Grundfunktionen entstehen (siehe auch [NI93]). Millionen Jahre, bevor Zeitmultiplex (TDM) vom Menschen erfunden wurde, erfand die Natur bereits Bursts als stochastisches Multiplex-Verfahren:
An M1, M2 und M3 (Bild 5c) können nun Klingelknöpfe angeschlossen werden, während an M1*, M2* und M3* Klingeln angeschlossen werden können. Wird z.B. M1 gedrückt, klingelt es nur bei M1* usw..
6. Entfernungsbestimmung mittels Echo
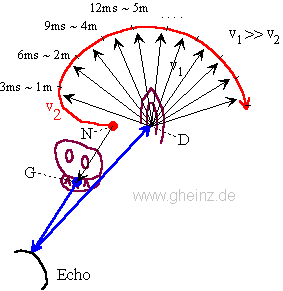
Bild 6: Interferenzmodell der Echo-Weltmodellierung einer Fledermaus
Vereinfachtes Modell zur Entfernungsbestimmung mittels Echo. Ein Generatorneuron N erzeugt eine Erregung, die sich auf zwei Wegen ausbreitet: Ein Teil erregt einen Schallgeber (Stimme) G, der andere Teil (rot) wandert langsam mit der Geschwindigkeit v2 radial um den Schallsensor (Ohr) D. Sobald das Echo wieder bei D eintrifft, breitet sich eine Erregung mit v1 zirkular aus. Der Ort der Interferenz korreliert dann mit der Entfernung. Wir erhalten eine Interferenzkarte der Außenwelt entlang der radial verlaufenden Fasern (sollte sich an Fledermäusen, Delphinen oder Walen nachweisen lassen).
Der Wal sendet z.B. Impulsgruppen im 128 Sekunden-Rhytmus aus, um seine Umgebung zu kartieren, dies entspricht einer interferentiell kartierbaren Weglänge von etwa 1/2 * 1500 m/s * 128 s = 96 km.
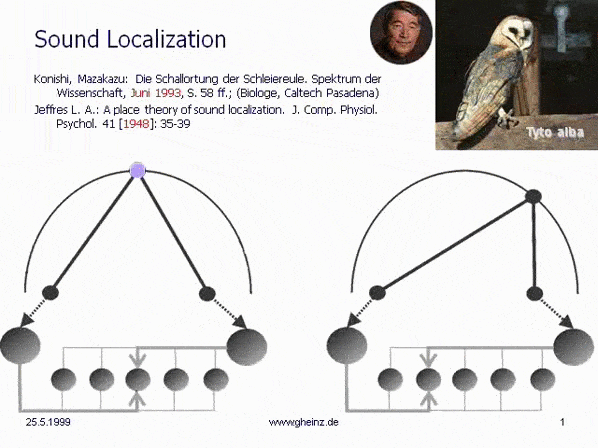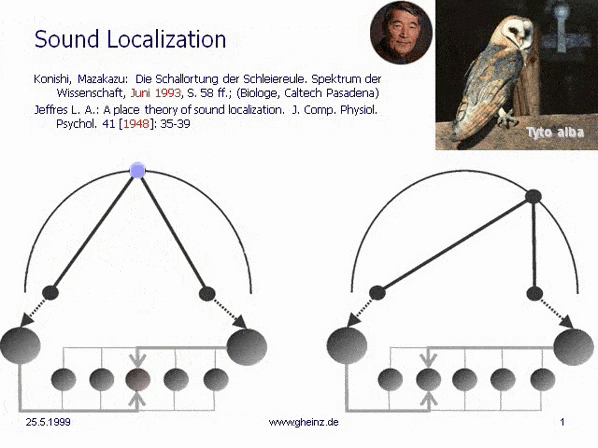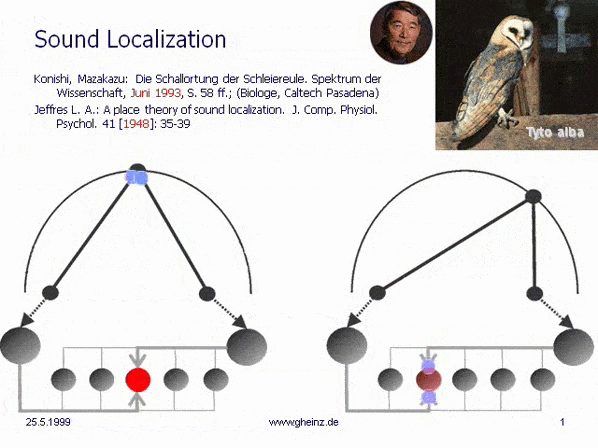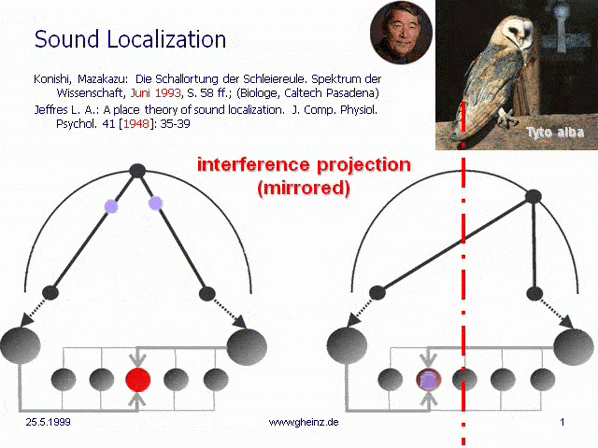
Bild 7: Mark Konishi's* Modell der Schallortung, vereinfacht nach Lloyd A. Jeffress 1948. (Historisch der erste, intermediale Interferenzkreis). Wir bemerken, daß die (in diesem Fall eindimensionale) Erregungskartierung des Generator-Raumes spiegelverkehrt zur Kartierung des Detektorraumes auftritt. Ein weiter rechtsliegendes Geräusch wird von weiter links liegende Neuronen registriert. Dort besitzt das sog. Interferenzintegral den höchsten Wert. Die Projektion erscheint spiegelverkehrt.
*Konishi, M.: Listening with two ears. Scientific American (April 1993), p. 66-73
8. Spiegelverkehrte Körperprojektionen im Rückenmark - Penfields
'Homunculus' als hyperbolischer Interferenzkreis
Verglichen mit Deutungen der grauen Substanz in den Wirbelkörpern des Rückenmarks zur Erzeugung von Reflexen (vgl. Duus, P.: Neurologisch- topische Diagnostik, S.10ff.) zeigt die hyperbolische Form der Anordnung der nichtmyelinisierten, grauen Substanz im Rückenmark dem Schaltungstechniker, daß hierbei wohl Verzögerungszeiten eine dominierende Rolle spielen müssen. Die Frage ist, wofür?
Ein Interferenznetzwerk liefert physikalisch relevante Indizien für die Entstehung und Ausbildung von spiegelverkehrten Körperprojektionen zum/vom Cortex. Wie das Daumenexperiment zeigt, variieren bei Dehnung/Stauchung die Verzögerungszeiten gedehnter oder gestauchter Leitbahnen.
Nehmen wir an, ein Nervennetz besitzt rein funktionale Zuordnungen über Klingeldrähte. Wozu brauchten wir dann zwischengeschaltete Karten, wie den Homunculus? Diese wären eigentlich überflüssig, sollte da nicht ein ganz besonderes Problem bestehen, welches überhaupt erst durch interferenzielle Betrachtung erkennbar wird.
Nehmen wir dazu weiter an, daß ein Klingeldrahtmodell zwischen Gehirn und Körper so viele Axonen benötigen würde, daß diese nicht durch den Wirbelkanal passen. Ein Interferenzmodell spart hingegen Axonen ein, da 'Bilder' (spiegelverkehrte Projektionen) auf viel weniger Leitbahnen übertragen werden können. Verbleibende Axonen passen durch die Wirbel im Rückenmark.
Genau hier entsteht ein Schnittstellenproblem: Bei jeder Kopfkippung oder -drehung würden die Abbildungen des Körpers im Kopf mitwandern und verrutschen - zwischen Cortex und Körper könnten interferenziell keine Daten ausgetauscht werden, weil diese bei jeder Halsdehnung oder Körperdrehung wechselseitig an einen anderen Interferenzort gesendet werden würden.
(Man stelle sich dazu einen Diaprojektor vor, der aus dem Vorderteil in das Heckteil eines Gelenkbusses leuchtet: Bei jeder Kurve und Bodenwelle verschiebt sich das Bild im Heck oder verschwindet ganz zu einer Seite).
Das Daumenexperiment erbrachte 1992 Gewissheit, daß bei einer Abspreizung des Daumens auch Interferenzorte verändert werden, gleiches muß also von Verbiegungen der Wirbelsäule erwartet werden.
Die Lösung der Natur ist wohl genial und einfach zugleich. Man schaffe eine Projektionsebene, auf die beide Seiten senkrecht blicken, die also von beiden Seiten (Hirn wie Körper) fokussierbar ist (siehe Movement und Zooming). Bei unserem Gelenkbus wäre das z.B. eine Leinwand, die wir mitten im Gelenk aufspannen. Diese kann für beide Seiten etwa senkrecht angeordnet werden. Schon verrutschen Abbildungen (motorische, wie sensorische) nicht mehr so stark. Aber dieses Modell ist nur symbolisch aufzufassen, konkret verhalten sich die Dinge anders.
Durch Leitgeschwindigkeitsvariation der Glia im Cortex können Abbildungen auf definierte Gebiete nachfokussiert werden - trotz Bewegung.
Die als motorischer und sensorischer Cortex [Love & Webb 1992, S. 19: 'Homunculus'] (siehe z.B. auch Wikipedia) bekannte Zone zwingt bei interferenzieller Betrachtung zur Schaffung einer notwendigen Koppelstelle zwischen Organen (Cortex und Körper), die beweglich miteinander verbunden sind.
Um zu einer Idee zu kommen, wie die Natur dieses technische Rätsel im Rückenmark löst, betrachten wir die Leitbahnen und Nervenquerschnitte im Rückrat. Markieren wir rot, grün und blau die Wellenfronten eines Pulses, dann lassen sich dargestellte Beziehungen finden.
Die Grundidee eines Interferenzmodells erzeugt grob und spiegelverkehrt eine Höhenzuordnung von Penfields Homunculus. Außerdem erzeugt es eine (flächige) Kartierung, die den Homunculus in der vorn/hinten-Richtung erweitert, wenn angenommen werden kann, daß mehr als zwei Axonen wirken. Es wäre denkbar, daß dies in der Evolution oder in der Individualgenese eine Rolle spielt: ein halsloser Körperbau bräuchte keinen Homunculus auszubilden.
Gardners 'reflex pathway' wird wie dargestellt interpretiert. Für das Modell geeigneter wäre allerdings eine bidirektionale, sowohl sensorische als auch motorische Einkopplung in das Rückenmark gleichzeitig von vorn und von hinten (c. dorsalis, c. ventralis) - ohne Richtungsunterscheidung. Dabei wäre eine Zwischenumsetzung im ganglion spinalis funktionell nicht bedeutsam. Es sei allerdings darauf verwiesen, daß eine beidseitig efferente und afferente Einkopplung bislang unbekannt zu sein scheint und noch nachgewiesen werden muß.
Der gut bekannte Seitenwechsel innerhalb der medula spinalis ist für das Modell nicht relevant. Diesen erzeugt die Dynamik des Modells selbst. Ein bei C4 oder S6 von rechts eingekoppelter Puls wird im Kortex links erscheinen und umgekehrt.
Ebenfalls nicht relevant ist die Frage, auf welchen Wegen oder Bahnen im Detail die Impulse den Cortex erreichen. Relevant hingegen ist, daß alle Signale gleichartig verzögert werden und daß in der medula spinalis kein zusätzlicher Seitenwechsel im Nervenstrang stattfindet. Eine physisch reale Kreuzung der Bahnen, wie sie in medizinischen Lehrbüchern zu finden ist, würde ein anderes Modell erfordern.
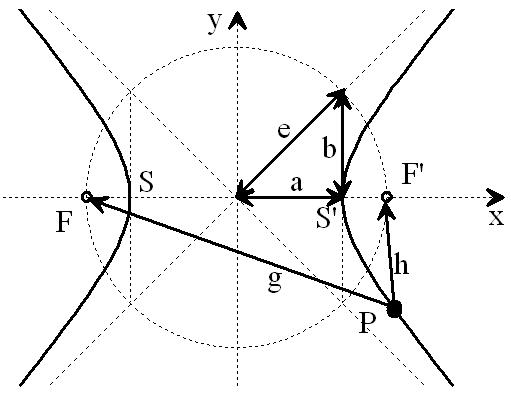
Bild 8a: Hyperbel aus NI93, Kap.3, S.77 (mit Hervorhebungen). Der Scheitelpunktabstand SS' = 2a = |g - h| bestimmt die Wege- oder Laufzeitdifferenz eines beliebigen Punktes P auf der Hyperbel nach deren Brennpunkten F und F'. Der Kreis mit dem Durchmesser 2e charakterisiert den Abstand der Brennpunkte F, F'
Wird nun der Scheitelpunktabstand 2a der Hyperbel variiert, ändert sich die Laufzeitdifferenz |g - h| der neuen, zugehörigen Hyperbel entsprechend. Enger beieinander liegende Scheitelpunkte SS' assoziieren mit einer geringeren Laufzeitdifferenz, weiter voneinander entfernte entsprechend mit höherer Laufzeitdifferenz. Siehe dazu auch das parametrische Plotbild mit eingetragenen relativen Längendifferenzen auf Seite 78 in [NI93] Kap.3.
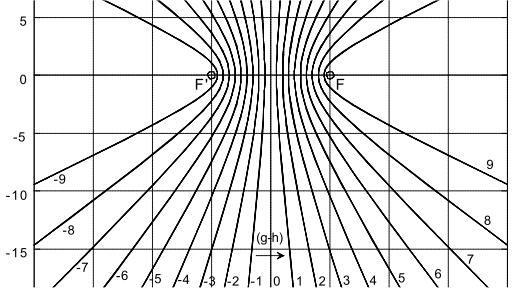
Bild 8b: Hyperbelschar aus NI93, Kap.3, S.78. Die Wegedifferenzen (g-h) entsprechen den Laufzeitdifferenzen, vermittelt über die Leitgeschwindigkeit der Fasern.
Kommen nun zwei Signale eines Ursprungsortes von oben und unten in den Hyperbelzweig und treffen sich diese an einem Ort auf P, so können die Signale mit einer neuen Laufzeitdifferenz 2a = |g - h| an die Brennpunkte weitergegeben werden. Sie können dann über die daneben liegende weiße Substanz (myelinisierte Fasern) in Richtung Cortex geleitet werden.
Spinnt man diesen Gedanken weiter, so entstehen im Cortex Körperprojektionen, die den an den verschiedenen Wirbelkörpern einmündenden Fasern zugeordnet sind. Dazu kann man zum Beispiel annehmen, den Brennpunktabstand FF' = 2e konstant zu halten durch Variation des Anstiegs der gestrichelt eingezeichneten Tangenten b = sqrt(|e² - a²|). Aber um dieses Modell zu verfeinern, wären deutlich weitergehende Untersuchungen an der medula spinalis erforderlich.
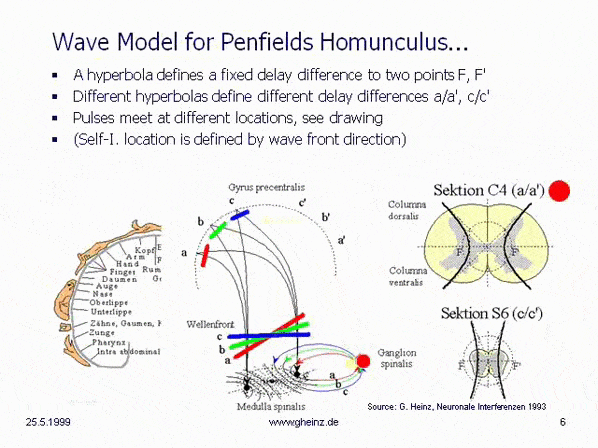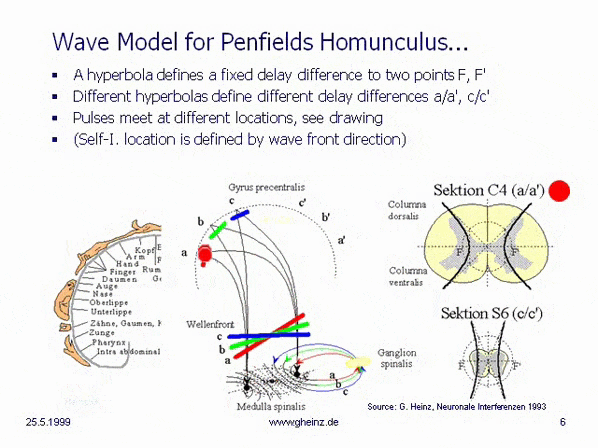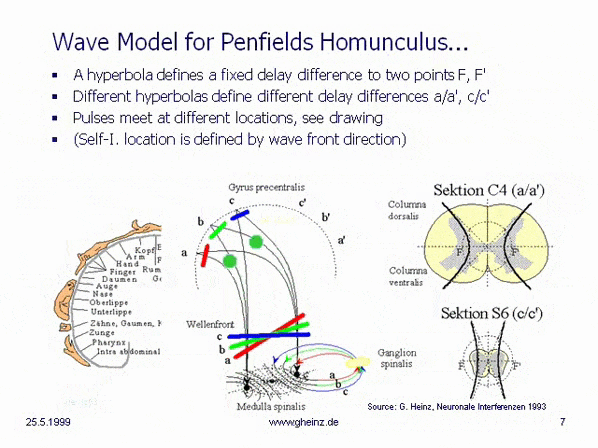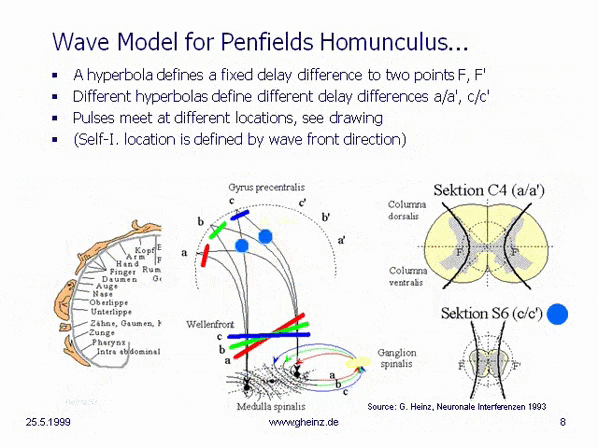
Bild 8c: Modell hyperbolischer, spiegelverkehrter Körperprojektionen des Rückenmarks. Vereinfachtes Modell der Medulla spinalis. Quelle: Heinz, G.: [NI93], Kap.12, S.251-253. Referenzen: Schmidt, R.F., Thews, G.: Physiologie des Menschen. 24. Auflage, Springer- Verlag 1990, S.105 sowie Rauber/Kopsch: Anatomie des Menschen; Band III: Nervensystem, Sinnesorgane. Georg Thieme Verlag Stuttgart, 1987, S. 299
Wird angenommen, daß die Dicke des Rückenmarks höhenabhängig variiert, so benötigt eine hyperbolische Projektion [NI93] Kap.3, S.76 ff. im Homunculus [NI93] Kap.12, S.251 ff. in dargestellter Art eine sich verringernde Laufzeitdifferenz mit nach unten abnehmender Dicke des Rückenmarks, Schnitt C4 (a/a') zu Schnitt S6 (c/c'). (Berechnung: siehe Wikipedia/ Hyperbel). Dies hat zur Folge, daß die Wellenfronten (rot, grün, blau) verschiedene Interferenzorte ansteuern. Bei gleich angenommenen Neuroneneigenschaften ist für Schnitt S6 (c/c') die Laufzeitdifferenz geringer als für Schnitt C4 (a/a'). Siehe dazu auch Bilder des Rückenmarks in der Wikipedia.
Eine von S6 blau dargestellte Wellenfront stiege zwangsläufig nach c oder c' auf, während von C4 bei größerer Laufzeitdifferenz eine schrägere Welle nach a bzw. a' aufsteigen würde. (Die Erregungswahrscheinlichkeit ist in dem Gebiet maximal, in welchem Gleichzeitigkeit des Eintreffens der Pulse herrscht.) Somit entsteht aus der Anatomie zwangsläufig eine Ortszuordnung, die in groben Zügen nur dem motorischen und sensorischen Areal von Penfields 'Homunculus' entsprechen kann.
Dieses einfachste, durch Laufzeitmessungen zu verifizierende Interferenz-Modell generiert damit im wesentlichen folgende Eigenschaften:
die anzutreffende, spiegelverkehrte Körperprojektion in den sensorischen wie in den motorischen Cortex die für den Homunculus typische Höhenzuordnung eine Entkopplung der Interferenzintegrale (Karten) zwischen Cortex und Körper
Überraschend erscheint die Tatsache, daß sowohl die notwendigen Zuführungen (c. ventralis, c. dorsalis) an der richtigen Stelle vorhanden sind. Nochmehr überrascht allerdings, daß sich sogar die graue Substanz der m. spinalis in der genau passenden Hyperbel-Form anordnet. Die Sektion C4 erweckt den Eindruck, hier seien im unteren Teil zwei Hyperbelanpassungen möglich. Die evolutionäre Idee dahinter ist noch unklar, es kann vermutet werden, daß sich hier die motorischen von den sensorischen Arealen absetzen, bekanntlich liegen diese im Cortex parallel zur Zentralfurche nebeneinander.
Es ist darauf hinzuweisen, daß dieses Modell mit lediglich zwei nach oben gehenden Fasern extrem vereinfacht ist. Es wäre zu erwarten, daß eine wesentlich größere Anzahl von Nervenfasern an der Interaktion beteiligt ist.
Da Nervennetze äußerst sensibel auf winzige Laufzeit- oder Längenveränderungen reagieren, sind andere Interpretationsmöglichkeiten eher nicht zu erwarten.
9. Ausbalancieren eines menschlichen Skeletts
Mit Rosenblatts 'Perceptron' gelang es in den Fünfzigern erstmals, eine Maschine zu schaffen, die einen einzigen Besenstiel ausbalancieren kann. Stellen wir nun zehn (kleine) Besenstiele übereinander, so wird uns die regelungstechnische Unmöglichkeit bewußt, die unser aufrechter Gang in sich birgt.
Mit Mitteln lokaler Regelsysteme ist es wohl nicht möglich, einen aus knapp 10 Gelenkteilen bestehenden, instabilen Turm so auszubalancieren, daß er stabil stehen kann. Regelvorgänge zwischen den Gelenken würden sich gegenseitig aufschaukeln, Stabilität des Gesamtsystems kann mit lokalen Regelalgorithmen wohl kaum erreicht werden. Wo also ist eine Lösung zu finden?
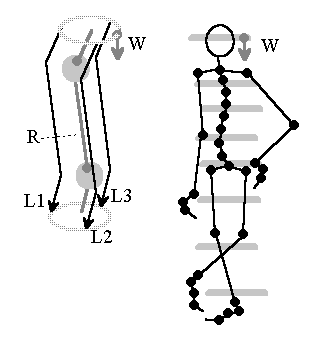
Bild 9: Modell eines sich selbst ausbalancierenden Gliederkörpers. Quelle: [NI93], Kap.12, S.250
Denken wir an das Daumenexperiment, so könnte eine virtuelle Wellenfront helfen, die vom Gleichgewichtsorgan im Kopf abwärts läuft und an der sich lokale Muskelgruppen ausrichten.
Wird vorausgesetzt, daß wenigstens drei Nervenfasern L1...L3 in angedeuteter Weise existieren, kann eine (virtuelle) Welle genutzt werden, um das System zu stabilisieren. Eine periodische Wiederkehr einer vom Gleichgewichtsorgan auf mehreren Nervenbahnen abwärts laufenden Wellenfront W wird vorausgesetzt, deren Wellengradient die Neigung des Gleichgewichtsorgans wiederspiegelt. Lokale Muskelgruppen könnten entsprechend ihrer von der Wellenfront abweichenden Relativlage nachregeln.
Dem einfachen Modell fehlen allerdings noch weitere Komponenten: Wie kann gewährleistet werden, daß alle Skelettmuskelgruppen mit anteilig proportionaler Kraft agieren? Wie kann das System in die Hocke gehen? Hier wäre noch harte Detailarbeit zu leisten.
Der einfache lokale Algorithmus zur Erlangung globaler Kontrolle lautet: Jedes Element muss seine Richtung orthogonal zur Wellenfrontrichtung ausrichten, vorausgesetzt, die Wellenfront erscheint periodisch.
10. Das visuelle Systems (chiasma opticum)
Schon in der Antike stellte man sich die Frage, wie die Welt, die auf der Netzhaut gespiegelt erscheint, zurückgespiegelt werden könnte. Arbeiten die Neuronen zwischen Retina und Visual Cortex nicht als Klingeldrähte, dann spiegelt ein Interferenznetz die Information nochmals. Es muss dabei wesentliche Funktionen unseres Sehens realisieren, wie Zooming und Movement.
Haben Sie schon einmal ein weißes Segelboot aus der Ferne fotographiert? Und auf dem Photo war anschliessend nur ein winziger, weisser Punkt zu sehen, obwohl Sie sogar die Personen auf dem Boot klar erkennen konnten? Offenbar kann unser Auge zoomen.
Es ist uns nicht bewußt, aber ständig muß unser visueller Cortex (VC) Bider zoomen, drehen, skalieren oder vervollständigen. Erst dann können wir sie erkennen. Nie sehen wir eine Person exakt so, wie sie im Personalausweis abgebildet ist.
Aber die optische Abbildung im Auge liefert keine Zoomfunktion. Für die Bildvergrößerung (Zoom) kommt nur die Variation der Hintergrundgeschwindigkeit im Interferenznetz zwischen Auge und visuellem Cortex (VC) in Frage. Wie das gehen könnte, zeigt ein Zoom-Experiment. Auch können Glia-Potentiale kleine Delay-Variationen im Sehnerv verursachen: Damit läßt sich das Bild bewegen. Siehe dazu auch eine Simulation zum Movement eines Bildes.
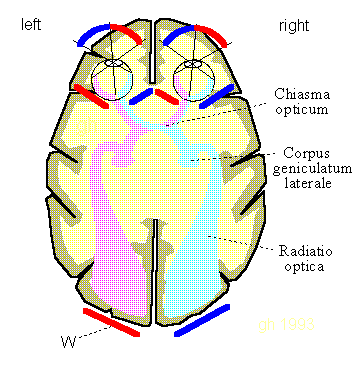
Bild 10.1: Sehnervensystem. Zufälligerweise zeigt die Orientierung von Projektionsflächen W (rot und blau) bekannte Abbildungsorte. Quelle: [NI93] Kap.12, S.247
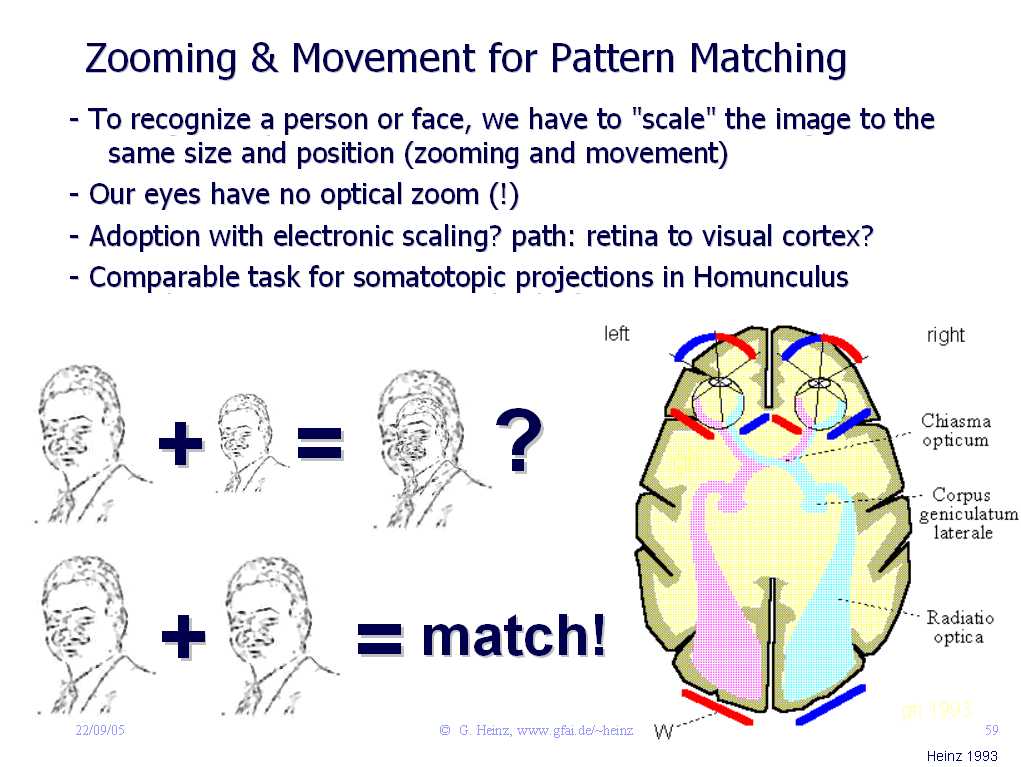
Bild 10.2: Das Auge liefert keine Zoom-Funktion. Bleibt nur das "Corpus geniclatum laterale" als cortikaler Bildprojektor! Source: Israel-lectures, 2005, (Link).
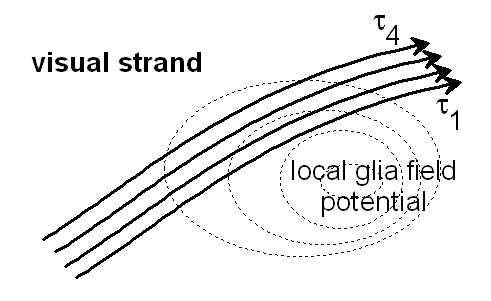
Bild 10.3: Unter dem Einfluß eines lokalen Feldes der Glia könnten unterschiedliche Verzögerungszeiten τ1 ... τ4 zu Zooming und Movement-Effekten im Sehstrang (visual strand) führen. Siehe auch IWINAC 2005, Fig.7, (Link)
Es wäre ein Hinweis auf ein projizierend abbildendes Interferenzsystem. Eine Aufnahme der realen Delay-Struktur könnte genutzt werden, um die Spezifik des Projektionsraumes zu berechnen.
Aber ist es denkbar, daß die Verzögerungszeiten von Neuronen im Corpus geniclatum laterale direkt gesteuert werden? Es ist wenig wahrscheinlich. Neuronen ändern nicht einfach so ihre Verzögerungszeit.
Auch die spiegelbildliche Projektion des optischen Systems ist eigentlich nur über interferentielle Ansätze nachvollziehbar. Die Wellenlänge der Nervenimpulse im visuellen Cortex beträgt etwa 0.1 Millimeter, die Segmentierung des VC liegt in derselben Größenordnung. Siehe weitere Details unter [NI93], Kap.5, S.114
Wenn wir versuchen, den Blick zwischen zwei verschiedenen Objekten auf dem Tisch wechseln zu lassen, wird die relative Position beider Objekte auf der Retina (Netzhaut) dieselbe sein, nachdem der Gegenstand jeweils fokussiert ist.
Um beide Objekte getrennt wahrnehmen zu können, ist es nötig, beide Objekte im Cortex in einem einem Weltmodell anzulegen, in welchem beide Objekte örtlich verschieden (z.B. nebeneinander) repräsentiert sind.
Die unter Movement dargestellte Verschiebung der Karte bei variierendem Delay der Kanäle kann helfen, dieses Problem zu lösen. Die nötige Delay-Variation könnte z.B. aus der Steuerspannung (siehe Pegelgenerierung) der Augenmuskeln gewonnen werden.
Dem Corpus geniculatum laterale kommt dabei die Bedeutung eines räumlichen Bildprojektors im VC zu.
Dieselbe Idee wie beim Homunculus kommt bei den Augen zum Tragen: auch diese "nehmen die Abbildungen bei Bewegung der Augenmuskeln mit". Hier aber ist der Effekt erwünscht - wie ein Projektor leuchten die Augen abhängig vom Blickwinkel in eine andere Zone des visuellen Cortex, wenn die Augenmuskeln direkt die Glia ansteuern, bewegt sich die Abbildung (Movement).
Da die Augen nie ruhen, entsteht über Interferenzintegrale im visuellen Cortex ein "Bild" der Umgebung, welches wesentlich größer ist, als der Teil, den die Augen unmittelbar zu einem einzigen Zeitpunkt fokussieren. Dies erklärt unsere Weltmodellierung: wir wissen stets, was um uns herum vorgeht, obwohl fixierte Augen nur einen winzigen Bereich der Umgebung wahrnehmen würden.
Sollte die radiato optica auch seitliche Ausläufer haben, die nicht der gezeigten Wellenfrontrichtung entsprechen können, dann ist dies ein sicherer Hinweis darauf, daß damit Bewegungen im Bildfeld detektiert werden können.
Weil die Wellenfrontrichtungen dort aber zur "Projektionswand" fast senkrecht stehen, können diese Bereiche keine sinnvollen Bildprojektionen erhalten. Aber welche Aufgabe könnten sie haben?
In Kap.5, S.99 von [NI93], Kap.12, S.263, finden wir eine mögliche Antwort. Sie könnten schnelle Bewegungen außerhalb des Sichtfeldes detektieren!
Allerdings wäre zu erwarten, dass die VC dann umfangreicher ausfallen würde als hier dargestellt.
Überall, wo wir spiegelverkehrte Karten im Nervensystem finden, ist oder war ein projizierendes Interferenzsystem am Werke, um diese Karten auszubilden.
Wir erahnen, daß der Interferenzansatz in allen Richtungen Möglichkeiten bietet, unser Nervensystem zu analysieren:
"Die Welt ist erkennbar!"
11. Erkrankungen des Nervensystems
Ein Ergebnis der theoretischen Untersuchungen an Interferenzschaltungen wäre, daß neuronale Kommunikation nicht nur durch Durchtrennung von Nerven, sondern auch durch parametrische Schwankungen von Laufzeit oder Refrakterität oder durch Veränderung z.B. der Länge eines Nervs gestört wird. Chirurgisches Zusammennähen eines Nervs wird z.B. nur dann erfolgreich sein, wenn Laufzeiten einzelner Bahnen relativ zueinander unverändert bleiben, weil nur dann neuronale Projektionen erhalten werden können.
Ein anderes Ergebnis bestünde in der Erkenntnis, daß winzige, parametrische Schwankungen der Leitgeschwindigkeit ausreichen, um nervliche Abbildungen zu zoomen, zu bewegen, zu löschen oder überzubelichten (Interferenzüberlauf). Tunnelblick kann z.B. aus kleinen Schwankungen der Leitgeschwindigkeit zwischen Auge und VC resultieren (siehe Zooming). Pharmaka, die Leitgeschwindigkeit oder Refraktärzeit verändern, stören das nervliche Kommunikationssystem, da Quellen und Ziele nicht mehr exakt miteinander kommunizieren können.
Drastische Veränderungen der Leitgeschwindigkeit z.B. durch Demyelinisierung (z.B. bei Multipler Sklerose) kann nur dann zu ausfallender Kommunikation führen, wenn das Nervensystem als Interferenznetzwerk verstanden werden kann.
12. Sensibilitätserhöhung der Hand
Die Schärfe einer Projektion variiert bei Veränderung des Abstands. Umso flacher die Wellen einlaufen, umso unschärfer wird die Abbildung. Die schärfste Abbildung entsteht beim geringstem Abstand, siehe eine Simulation dieses Effekts hier.
Offenbar kam auch die Evolution zu diesem Schluß. Betrachten wir die Hand, dann fällt auf, daß Nervus ulnaris und Nervus medianus über den sog. Bogen umgelenkt werden und dann wieder zurück nach oben führen.
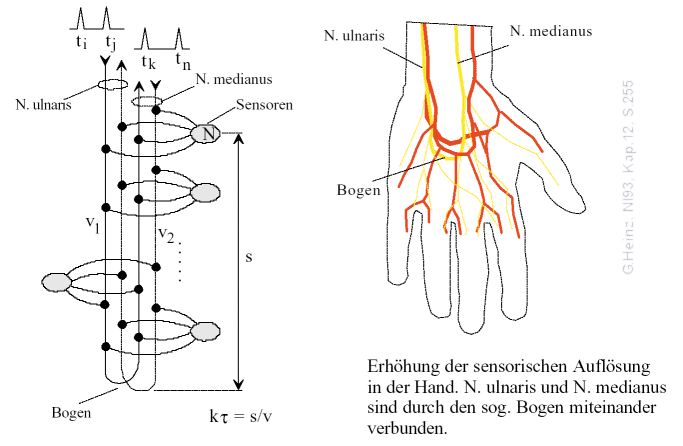
Bild 11: Gegenläufige Fasern des N. ulnaris und des N. medianus sorgen in der Hand dafür, daß die höchste Schärfe und Sensibilität erreicht wird. Details siehe [NI93] Kap.12, S.255
Es kann nur einen Zweck für diese erstaunliche Anordnung geben. Wir alle wissen, daß unsere Sensibilität in der Hand am höchsten ist, hier können wir Berührungen im Millimeterbereich zuordnen.
Betrachtet man das Bild länger, dann bemerkt man einen Widerspruch. Kommender und gehender N.ulnaris heißen nach dem Bogen N.medianus.
13. Wie ein Regenwurm schlängelt
Strickleiternervensystem als Interferenznetzwerk betrachtet.
Mit langsamer und langsamster Leitgeschwindigkeit eröffenen Nervenfasern die Möglichkeit, scheinbar komplexe Funktionen mit einfachsten Mitteln auszuführen.
Aus der Anatomie des Regenwurms wissen wir, daß er ein rudimentäres Strickleiter- Nervensystem besitzt. Es besteht aus paarigen, längs zur Körperachse verlaufenden Bahnen, die quer zur Körperachse über Kommissuren verbunden sind. Auch andere Insekten weisen ein mehr oder minder gut erkennbares Strickleiternervensystem auf, wie Gliederfüßer und Bärtierchen.
Unter der Annahme, die Strickleiter enthält Nervenfasern, die recht langsam leiten, kann damit die Schlängelbewegung als Interferenznetz modelliert werden.

Bild 12: Eine wellende Wellenfront bringt den Wurm zum Schlängeln. Bildquelle: [NI93] Kap.12, S.264
Wie aber kann der Wurm schlängeln? Welche Rolle spielt dabei die Strickleiter?
Am Anfang steht die auffällige Anatomie dieses Nervensystems. Welche Beziehung hat sie zu dessen Funktion? Können wir darin ein Interferenznetzwerk erkennen?
Man weiß, daß die am Anfang der Strickleiter befindlichen Oberschlund- und Unterschlundganglien (ganglia pharyngealis superior; OSL und OSR im Bild 13) das Strickleiter-Nervensystem steuern. Aber wie?
Wenn wir annehmen, das linke obere Rachenganglion (OSL) sendet einen Impuls (oder eine Impulsfolge) aus, so läuft dieser entlang des linken Teils der Strickleiter über GL1, GL2 und folgende Ganglien weiter, siehe Bild 13.
Allerdings gelangt der Puls auch zeitverzögert in das rechte Rachenganglion (OSR) und läuft nun auch dort zeitverzögert entlang des rechten Teils der Strickleiter über GR1, GR2 und folgende weiter.
Gleiche Verzögerungszeiten T1 und T2 vorausgesetzt, treffen die Teilwellen nacheinander in allen rechten Ganglien (GR1, GR2 ...) wieder aufeinander. Dort entsteht zwangsläufig ein höherer Schwellenwert, die Ganglien GR1, GR2 und folgende werden erregt. Sie werden nacheinander die betreffenden Muskeln MR1, MR2 und folgende stimulieren.
In Bild 13 sehen wir den eingefrorenen Zustand, wenn die Teilimpulse T1 und T2 gleichzeitig am Ganglion GR2 aufeinandertreffen. Der Muskel MR2 wird gerade stimuliert (orange).
Wir abstrahieren eine virtuelle, schräge Wellenfront (WF), die auf der linken Seite des Wurms vorangeht. Sie stimuliert die Muskeln der rechten Seite.
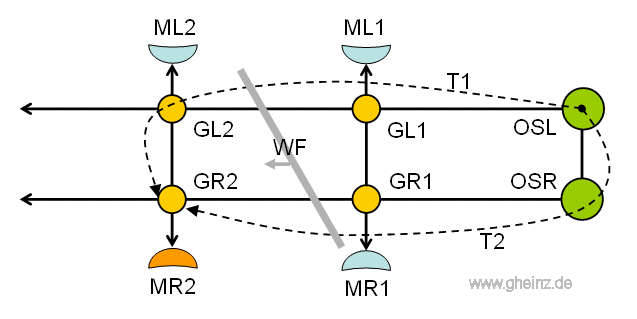
Bild 13: Strickleiter-Nervensystem als Interferenznetzwerk. Hier wird das Ganglion GR2 mit dem Muskel MR2 gerade erregt, wenn beide Pulswellenanteile T1 und T2 gleichzeitig vom linken oberen Rachenganglion OSL eintreffen. Details siehe [NI93] Kapitel 12, S.264
Wir gehen davon aus, dass die Kommissuren, also die Rechts-Links-Verbindungen der Strickleiter, jeweils die gleiche Verzögerungszeit haben.
Wir gehen außerdem davon aus, dass die Strickleiter symmetrisch aufgebaut ist, d. h. dass sich die Verzögerungszeiten der Abschnitte auf beiden Seiten nicht unterscheiden.
Letztlich ist es auch notwendig, dass die Ganglien, einmal erregt, die Muskeln mit langanhaltenden Potenzialen aktivieren können.
Wenn wir uns das zweite, rechte Ganglion (GR2) im Bild ansehen, wird deutlich, dass es höher erregt werden kann, wenn ein Impuls von T1 und ein Impuls von T2 gleichzeitig eintreffen. Genau dann ist die Wahrscheinlichkeit einer Stimulation des Ganglions am höchsten (orange).
Letztlich springt diese Erregung von Muskel zu Muskel auf der rechten Seite weiter und löst eine Kontraktion auf der rechten Seite des Wurms aus.
Analog dazu löst ein Impuls oder eine Gruppe von Impulsen vom OSR auf der rechten Seite eine fortschreitende Erregung der Muskeln auf der linken Seite aus.
Werden OSL und OSR nacheinander aktiv, beginnt unser Wurm zu schlängeln.
Werden OSL und OSR sehr schnell nacheinander oder gleichzeitig aktiviert, werden die Muskeln rechts und links nahezu gleichzeitig angespannt und der Wurm kontrahiert.
Dies funktioniert jedoch nur, wenn die Kommisurenbahnen aus gegenläufigen monodirektionalen Fasern statt aus bidirektionalen Fasern bestehen, sonst käme es zu einer refraktiven Impulsauslöschung, vgl [NI93] Kapitel 6, S. 144.
13.1 Strickleiter in einem Hauptstrang
Nun kann man in der deutschen Wikipedia nachlesen, daß die Strickleiter beim Regenwurm in einem Hauptstrang konzentriert ist, der den Wurm ventral (auf der Bauchseite) vom vierten Kopfsegment bis zum Schwanzsegment durchzieht, die Steuerganglien OSL, OSR liegen im dritten Segment.
Das mag zunächst verunsichern. Warum kam die Evolution auf diese merkwürdige Lösung?
Denken wir an das Daumenexperiment, dann kommt ein Verdacht auf. Beim Daumenexperiment wurde eine Veränderung der Verzögerungszeiten infolge einer Dehnung/Stauchung der Nervenfasern beobachtet.
Würden die Fasern der Strickleiter beim Regenwurm links und rechts außen verlaufen, käme es infolge der Schlängelbewegung ebenfalls zu starken Streckungen und Stauchungen der Nervenfasern und infolge dessen zu gegenläufigen Veränderungen der Verzögerungszeiten.
Offenbar entschied sich die Evolution dafür, auf konstante Verzögerungszeiten beider Seiten zu setzen, indem die Länge der verbindenden Kommissuren der Strickleiter minimiert wurde.
Wir erkennen, dass scheinbar komplexes Verhalten auf einfachste Verschaltungen reduziert werden kann. Es ist wahrscheinlich das einfachste Interferenznetzwerk, das im Tierreich beobachtet werden kann. Fachleute sollten in der Lage sein, die hypothetisch eingeführten, relativen Verzögerungszeiten mit einfachen Mitteln zu messen.
13.2 Beinsteuerung eines Insekts
Nun haben auch fliegende Insekten einen Gliederkörper, dessen Ganglien des Strickleiter-Nervensystems diesem Gliederkörper exakt zuordenbar sind. Das legt den Verdacht nahe, daß die Strickleiter auch hier eine entscheidende Rolle spielt.
In einem Schnittbild eines Fluginsekts bei Wikipedia fällt auf, daß an den Ganglien der Beinsegmente jeweils zwei kleine Stränge zur Beinversorgung abgehen. Es wäre also recht wahrscheinlich, daß auch deren Beine über die Strickleiter gesteuert werden.
Wie könnte nun das Interferenzmodell des Regenwurms erweitert werden, um auch noch die komplexe Steuerung der Beine zu übernehmen? Schließlich müssen die Beine nach vorn, hinten, oben und unten bewegt werden?
Sehen wir uns dazu zunächst noch einmal die Zeitfunktionen vom Regenwurm an.
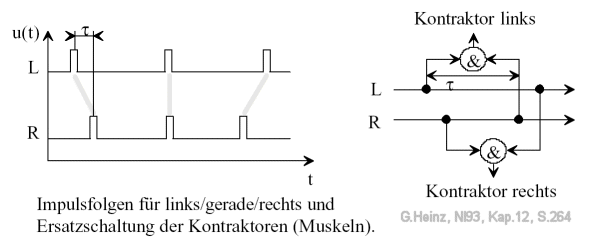
Bild 13.2: Zeitfunktionen und Ganglien im Strickleiter-Nervensystem des Regenwurms. Ein entgegengesetztes Vorzeichen der Verzögerung τ führt zur Ansteuerung der andere Seite. Die &-Zeichen sollen hier einen multiplikativen Verknüpfungstyp darstellen. "Kontraktor links" soll das linke Ganglion GL darstellen, "Kontraktor rechts" soll das rechte Ganglion GR darstellen. Bildquelle: [NI93] Kap.12, S.264
Im Bild 13.3 ist das Prinzip beim Regenwurm zu erkennen. Ein linker oder rechter "Kontraktor" wird ausgelöst, wenn die Laufzeitdifferenz τ exakt mit den ankommenden Impulsverzögerungen übereinstimmt.
Wie ist nun die Schaltung um die Beinsteuerung bei Insekten zu erweitern?
Können in einem Ganglion zwei verschiedene Laufzeitdifferenzen (oder Wellenfronten) pro Seite detektiert werden, die sich voneinander geringfügig unterscheiden, so wäre eine Ansteuerung des einen oder des anderen Detektors (des Beins) möglich, Bild 15.
Natürlich muß auch die Verbindung zwischen OSL und OSR doppelt ausgeführt werden, um die zwei unterschiedlichen Wellenfronten zu erzeugen.
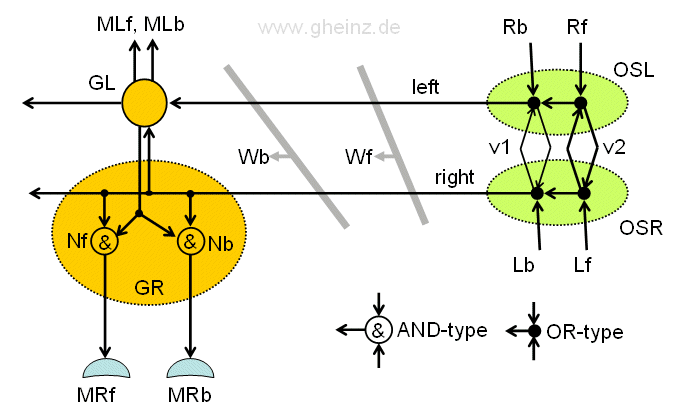
Bild 13.3: Strickleiter-Nervensystem eines Fluginsekts. Ein Beinganglion GR und der Signalgenerator OSL, OSR im Detail. Unterscheiden sich die Wellenfronten Wb und Wf, so lassen sich damit zwei verschiedene Detektoren für die vor/rück-Bewegung der Beinmuskeln MRf, MRb ansteuern, deren Abgriff auf der Strickleiter geringfügig variiert. GL, GR: Ganglien für linkes/rechtes Bein; OSL, OSR: Linkes/rechtes Unterschlund-Ganglion; v1, v2: Leitgeschwindigkeiten; Nf, Nb Detektor-Neuronen.
Das Bein ließe sich damit unabhängig nach vorn oder nach hinten bewegen. Dazu wären die Ganglien um eine zweite Detektorschaltung für jede Seite (links und rechts) zu erweitern.
Zu den AND- und OR- Neuronen: Zwei verschiedene Typen werden angenommen. Der AND-Typ soll multiplikativer Art sein, hier werden gleichzeitig an allen Eingängen Pulsspitzen gebraucht, damit das Neuron pulst. Typ OR soll jeden Impuls an einem Eingang auf die Ausgänge weiterleiten. (Wie auch in Bild 13.2 ist auch in Bild 13.3 eine doppelte Verbindung der Ganglien GR und GL dargestellt, die auch beim Regenwurm gebraucht wird, um refraktive Auslöschung gegeneinander laufender Pulse zu verhindern.)
Pulsgeber OSL, OSR: Wie zu erkennen ist, wäre der Pulsgeber beider Seiten doppelt auszuführen, für vorwärts (Index f) und für rückwärts (Index b). Eine Signalrückkopplung zwischen OSL und OSR mit Selbsterregung ist dann nicht zu befürchten, wenn die Refraktärphase der Neuronen vom OR-Typ hoch genug wäre.
Zur Funktion des Pulsgebers: Zwei unterschiedliche Leitgeschwindigkeiten v1 und v2 mögen zwei verschiedene Verzögerungen auf der Kommissuren-Leitbahn (der Länge s) zwischen OSL und OSR erzeugen, mit τ1 = s/v1 und τ2 = s/v2. Wir nehmen an, daß v1 < v2 ist. Die Leitbahnen v1 sind deshalb dünner dargestellt, als die für v2. Läuft ein vorwärts-Puls bei Rf ein, wird v1 aktiviert und erzeugt eine Wellenfront Wf, analog erzeugt ein rückwärts-Puls an Rb über v2 eine Wellenfront Wb.
Detektoren GR, GL: Ein erstes Detektorneuron Nb würde die Wellenfront Wb detektieren und den Bein-rückwärts Muskel MRb aktivieren, ein zweites Detektorneuron MRf würde Wellenfront Wf detektieren und den Bein-vorwärts Muskel MRf aktivieren.
Das Detektorpaar Nb, Nf kann prinzipiell identisch sein. Es wäre lediglich nötig, die Abgriffe des Detektor-Paars auf der Strickleiter geringfügig unterschiedlich zu wählen.
Eine besondere Rafinesse dieser Schaltung soll noch erwähnt werden, welches bei Insekten beobachtet werden kann. Wie beim Regenwurm laufen die Pulse nach hinten weiter. Sie erregen dabei fortfolgende Ganglien dieser Seite. Jedes Bein erhält damit mit leichter Verzögerung denselben Befehl: Gehe vorwärts oder gehe rückwärts. Die Bewegung der Beinpaare untereinander wird damit automatisch koordiniert.
Soll das Bein noch nach oben oder unten bewegt werden, wären zwei weitere Detektoren pro Bein nötig. Oder die auf/ab-Bewegung wird mit der vorwärts/rückwärts-Bewegung gekoppelt. Vorwärts hebt sich das Bein, rückwärts senkt es sich ab (das hätte allerdings den Nachteil, daß das Tier nicht rückwärts krabbeln könnte). Aber hier wird es spekulativ, hier wären mikroskopische Analysen und detailierte Untersuchungen des Verhaltens einer speziellen Tierart gefragt.
Denken wir außerdem daran, daß in den Beinen noch ein Oberschenkelmuskel zu betätigen ist, wird schnell klar, daß es sich hier nur um ein sehr grobes Modell handelt. Die Darstellung aller Details würde den Rahmen dieser Darstellung allerdings erheblich sprengen.
An anderer Stelle steht über Interferenznetzwerke geschrieben: "Die Form codiert das Verhalten". Es scheint, daß dieser Satz auch hier gültig ist.
Es erstaunt immer wieder, welch genial einfache Konstruktionen die Natur für ein so komplex erscheinendes Verhalten ersann!
Im Buch "Neuronale Interferenzen" von 1993 (NI93) wurden in Kap.8b Schaltungen zur Sequenzanalyse mit Laufzeitleitungen entwickelt, vgl. S.181 (Bild 14.2).
Denken wir an die komplexen und präzisen Bewegungen eines Bauern, der eine Wiese mit einer Sense mäht, oder an eine Tänzerin, aber auch an alltägliches, wie Treppensteigen oder an Geräusche und Lauterkennung oder nicht zuletzt an Worterkennung und in deren Hierarchie Satzerkennung etc. so sind stets Analysatoren gefragt, die Sequenzen erkennen und analysieren können. Wie können wir uns derartige neuronale Schaltungen in einfachster Form vorstellen?
Wir gehen davon aus, daß eine hier zu analysierende Zeitfunktion pulsdichtemoduliert ankommt. Hohe Amplituden werden dabei in Pulse verwandelt.
Bild 14.1: Beispielhafte Pulswandlung eines Geräuschs, eines Lauts oder eines Wortes (symbolisch). Detektieren wir positive und negative Maxima, so erhalten wir eine Pulsfolge, die einige Merkmale dieser Sequenz charakterisiert.
Bild 14.2: Auszug NI93, S.181. Links Laufzeitdarstellung, rechts signaltheoretische Knotenabstraktion als FIR-Filter. Input ist eine Pulsfolge x(t), Output y(t) sei ein Impuls, wi seien Gewichte. q mag eine Pulsformung sein.
Zitat: "Grundgedanke ist der, daß ein auf τ-vielfachen abtastbarer Code auf einer kreisförmigen Bahn verzögert wird, in deren Mittelpunkt sich das Neuron befindet. Jeder Abgriff am Kreis besitzt gleichen Abstand vom und gleiche Laufzeit zum Mittelpunkt, sodaß die Laufzeit auf den Radialen kompensiert ist. Die zum Mittelpunkt führenden Abgriffe sind auf dem Kreis in τ-Vielfachen angeordnet. Stimulierend und hemmend eingestellte Gewichte wi am Neuron lassen sich so wählen, daß Erregung nur beim richtigen Code eintritt. Es sind mindestens n Impulse zur einmaligen Auslösung des Detektors erforderlich. n ist die Anzahl der Eingänge des Neurons."
Mit dieser Anordnung wäre es bereits möglich, periodische Zeitfunktionen zu detektieren (Töne). Mit mehreren derart geschalteten Neuronen ließe sich das Hörspektrum spektral zerlegen (zur Fourieranalyse mit verschiedenen τ).
Wie aber kann auf einfachste Weise ein Geräusch oder ein Wort erkannt werden?
Auf Seite 188 (NI93, Kap.8b) gibt es eine Antwort. Dazu sind die Gewichte der Schaltung entsprechend der herauszufilternden Pulsfolge zu modifizieren, siehe Bild 14.3.
Bild 14.3: Sequenzanalysatoren. Auszug NI93, S.189. Links ein radialer Sequenzanalysator, rechts eine axiale Variante. Hier sind die hoch bewerteten Gewichte grau, die nicht benötigten Gewichte schwarz dargestellt. Die Notation der Inputs in geschweiften Klammern ist von rechts nach links zu lesen, schwarz bedeutet 0, grau 1.
Denken wir uns nun die signaltheoretische Abstraktion einer in der Natur nicht vorkommenden Abtastrate mit τ weg, dann sind wir in der Realität angekommen. Es genügt, dem Neuron n über einen weiteren, generalisierenden Input (Bias) mitzuteilen, daß es die Gewichte des gerade angekommenen Lauts, Geräuschs, Wortes, einer Bewegung oder eines Verhaltens (allgemein eine Sequenz) erhöhen soll. In welcher Form die Natur dem Neuron mitteilt, die Gewichte zu übernehmen, sei dahingestellt. Eines ist allerdings klar: Um etwas zu lernen, ist stets ein auslösender Reiz (hier als Bias eingetragen) vonnöten, der dem Neuron mitteilt, relevante Gewichte zu erhöhen und nichtrelevante zu reduzieren, um den Lernvorgang fortzusetzen. Beim auslösenden Reiz kann es sich um das Klirren eines herunterfallenden Glases handeln oder um ein Stolpern, einen Unfall, eine Beobachtung (Aha!-Effekt) oder um was auch immer.
Zu beachten wäre, daß eine einmalige, vollständige Übernahme der Gewichte nicht zum Erfolg führen würde. Bereits in der nächsten, vergleichbaren Situation wird die zu detektierende Zeitfunktion (Trainimgsdaten) i.a. stark abweichen. Die Natur wird also langsam lernen müssen um die Gewichte langsam anzupassen. Zu beachten wäre auch, daß Gewichte sowohl erhöht, als auch verrringert werden müssen, um nicht zu riskieren, daß eines Tages alle Gewichte am Anschlag sind.
Beobachten wir ein Nervenfaserbündel mit Fasern verschiedener Leitgeschwindigkeiten, die auf ein Neuron zulaufen, Bild 14.3 rechts, so liegt hier eine zweite Art eines Sequenzanalysators vor. Diese Form ist in der Hirnrinde des Cortex wahrscheinlich millionenfach anzutreffen. Siehe dazu z.B. ein Golgi-Präparat von Ramón y Cajal im Eccles in Abb.I 2, S.20.
Vergleichen wir die Anordnung in Bild 14.3 links mit einer technischen Realisierung als FIR-Filter im Bild 14.2 rechts, dann wird klar, welch enormen Entwicklungsvorsprung die Biologie gegenüber der Technik noch hat. Während die Biologie mit ein oder zwei Neuronen auskommt, die Mikrometer groß sind und Nanowatt verbrauchen, braucht eine entsprechende technische Realisierung ein tausendfaches an Verlustleistung, Größe und Gewicht.
Was wir brauchen, um in diese Effiziensklasse der Biologie vorzudringen, wären analoge Laufzeitnetzwerke als Interferenznetze technischer Art. Grundvoraussetzung dafür wären einfachste Laufzeitleitungen analoger Natur. Nun wissen wir, daß es diese eigentlich schon gibt, denken wir an Polysil-Leitbahnen auf integrierten Schaltkreisen. Allerdings sind diese immer noch millionenfach schneller, als Nervenfasern, also immer noch sehr schnell. Das könnte von Vorteil sein, wenn wir an ultraschnelle Informatik denken, deren 'Neuronen' in Picosekunden pulsen. Hier gäbe es m.E. ein Fachgebiet, welches unbedingt förderwürdig wäre. Einzelne Firmen könnten die Voraussetzungen dafür finanziell wohl eher kaum bewältigen.
'Keinem Sterblichen ist es vergönnt, das Leben in der Zerstreuung physikalischer oder chemischer Substanz, in diffuser, wenn man will, geistiger Form zu erkennen, und wenn dies geschehen sollte, so würde dies gewiss der härteste Schlag sein, der die heutige, naturwissenschaftliche Anschauung treffen könnte.'
Rudolf Virchow
© Kopierrechte für diese Seite: Bilder können uneingeschränkt genutzt werden, wenn der Name des Authors und die Herkunft des Bildes als Webadresse dieser Seite sichtbar vermerkt sind.
Haben Sie Fehler gefunden?
Bitte benachrichtigen Sie mich per
E-Mail!
Vielen Dank im voraus!
File created Sept.30, 1995. Continued editions. Stylesheets introduced Jan.2024. Kap.12 und Kap.13 eingefügt, 2.2.2024.
Visitors since Dec. 2021: