G. Heinz
Einem Aufsatz Masakazu Konishis [1] zufolge gab Lloyd A. Jeffress [9] 1948 eine Prinzipschaltung an, die das akustische Ortungsprinzip von Schleiereulen beschreibt (Bilder 1 und 2). Es ist das Verdienst Mark Konishi's, den Jeffress'schen Ansatz 1993 popularisiert zu haben.
Dieser grundlegende Schaltkreis, heute würden wir ihn als "intermedialen Interferenzschaltkreis" bezeichnen, zeigt wichtige Merkmale der biologischen Informatik in einer neuen Sichtweise: eine Entsprechung zwischen einem Ort und den übertragenden Zeitfunktionen, einen Zusammenhang zwischen Code in Raum und Zeit.
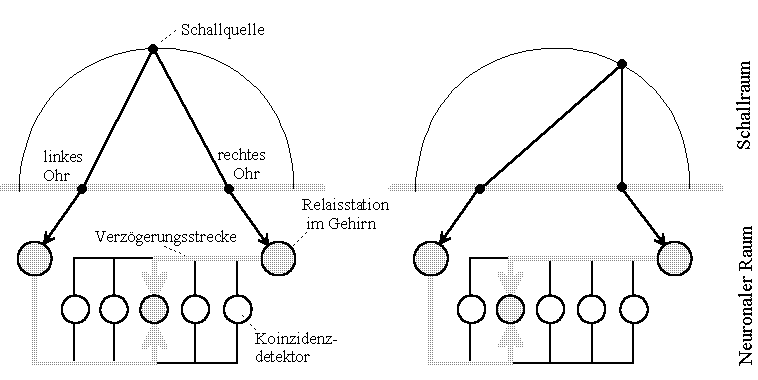
In Bezug auf Jeffress Bild 2, stellt Marks Version in Bild 1 eine vereinfachte Version von Jeffress dar. Und er schrieb über sinusförmige Schallwellen statt über pulsierende oder rauschende Zeitfunktionen. Das Problem bei Sinuswellen ist das entstehende Fremdinterferenzmuster, das die Lokalisation einer Quelle erschwert.
Bild 1: Zeichnung [1] von Konishi's Schallortung, 06/1993.
Zur Funktion: Liegt eine Schallquelle auf der Symmetrielinie zwischen beiden Ohren, so erreichen die im Ohr ("Relaisstation") in Nervenimpulse umgesetzten Signale zur gleichen Zeit Neuronen ("Koinzidenzdetektor") in der Mitte des Gehirns. Liegt die Quelle hingegen rechts versetzt, so treffen sich die Nervenimpulse weiter links im Gehirn. Multiplizieren wir nun an jedem Neuron die von links und rechts kommenden, i.a. zeitversetzten Zeitfunktionen (Konishi drückte es komplizierter aus), so wird nur das Neuron erregt, bei dem die Signale gleichzeitig erscheinen (hervorgehoben). Dabei genügt für die Multiplikation die Abstraktion, den Pulswert mit eins anzunehmen und Ruhephasen mit Null anzunehmen.
Wir entdecken folgende Eigenschaften eines Interferenzkreises (siehe auch [6], [7], [8]:
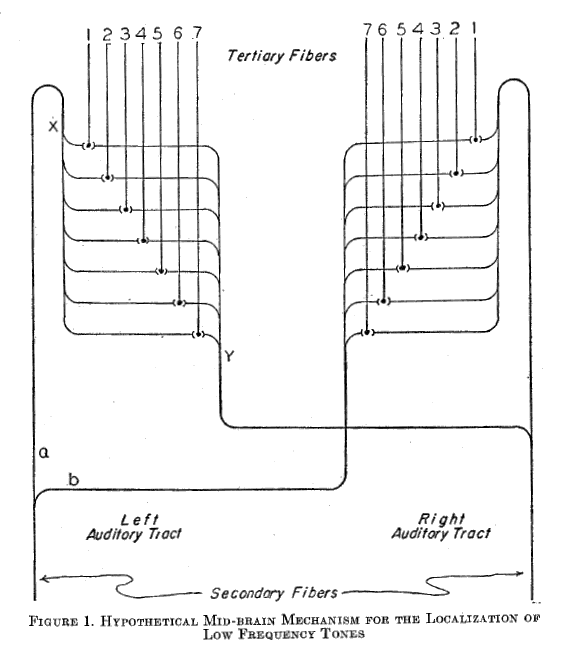
Bild 2: Darstellung von Jeffress 1947 [9] - historisch die Geburt eines nervlichen Interferenzkreises
Jeffress, wie Konishis Interpretationen beziehen sich leider auf für die Modellierung des Nervensystems ungeeignete, sinusförmige Zeitfunktionen. Neuronen geben nur pulsartige Signale ab. Siehe dazu auch einige Simulationen zu Wellen-Interferenzen.
Betrachten wir im Gegensatz dazu pulsförmige Zeitfunktionen (lange Pause und nadelförmiger Puls), so erkennen wir, daß beide Signalformen gegensätzliche Eigenschaften bei den Interferenznetzen markieren: Eine Betrachtung zu Fremdinterferenzen (klassische Analogie: Kreuzkorrelation) zeigt Eigenschaften der sinusförmigen Zeitfunktionen bei der Erklärung von Fremdinterferenz (Harmonie, Musik, Takt, Zeitgefühl), während pulsförmige Zeitfunktionen für Datenadressierung und Signalübertragung optimale Eigenschaften besitzen.
Allerdings treten in einem Nervennetz keine sinusförmigen Signale auf, diese finden wir eher in der Akustik (Beispiel akustische Kamera). Die nervliche Entsprechung stellen mehr oder minder dichte Pulsfolgen dar, deren geometrische Pulswellenlänge und deren geometrischer Pulsabstand (Entsprechung zur physikalischen Wellenlänge) variiert. Geometrischer Pulsabstand und geom. Pulslänge stellen die Schlüsselparameter von Interferenznetzen schlechthin dar: Sie entscheiden über fast alle Abbildungsqualitäten (mehr siehe [6]).
Interferenzielle Datenadressierung funktioniert dabei umso besser, je weniger dicht (sinusförmig) die Zeitfunktionen sind. (Nervenimpulse bewegen sich mit Geschwindigkeiten im Bereich von µm/s ... m/s, bei typischen Impulsdauern von 0.1 ms bis 100 ms), siehe Tabelle [8].
Konishi's Schaltung funktioniert nicht nur zwischen verschiedenen Medien. Nehmen wir an, der mit 'Schallraum' bezeichnete Raum bestünde ebenfalls aus Neuronen mit Verbindungen zu den 'Relaisstationen'. Die Eigenschaften des Netzwerkes würden sich kaum ändern. Auch dann würden wir eine spiegelverkehrte Erregungskartierung erhalten. Beide neuronalen Felder brauchten zu diesem Zweck nur über mehr als zwei Axonen verbunden zu sein. Diese Idee nahm (unabhängig von Jeffress und Konishi) 1992 Gestalt an, sie ziert das Titelblatt des Manuskripts "Neuronale Interferenzen", Bild 3.
Bild 3: Titelbild des Manuskripts 'Neuronale Interferenzen' [6] (1993) - ein monomedialer Interferenzkreis. Diese einfachste Interferenzschaltung liefert spiegelverkehrte, topische Projektionen und Abbildungen zwischen Sendefeld S und Empfangsfeld M. Vorausgesetzt werden in IN grundsätzlich verzögerungsbehaftete Leitbahnen.
Die Frage, warum so bemerkenswerte Eigenschaften fünfzig Jahre lang übersehen wurden, führt auf dem Pfad der Computerpioniere zurück zu McCulloch/Pitts.
Mit den Arbeiten von John von Neumann, aber auch mit denen von Conrad Zuse kam zu Beginn der 1940-er Jahre die Fiktion vom Computer auf. Potentiale wurden ein bevorzugtes Mittel der Leitbahndarstellung. Die Darstellung verzögernder Leitbahnen kostet viel mehr Rechenaufwand, als die Reduzierung einer Leitbahn auf einen Knoten. Das Leibnizsche Binärsystem (hundert Jahre später als Boole'sche Algebra bezeichnet) wird abstrahiert von diskreten und fixen Werten oder Zuständen (States) unter Weglassung von Zeitfunktionen. Die Erfindung eines "Takts" (clock) machte dies möglich. Der Computer wird damit von Anbeginn an Werte oder Zustände - an Knotenabstraktion und an diskrete Zeitpunkte gebunden.
Auch benutzten Neuroforscher unbedarft die in elektrischen Schaltungen übliche Knotenabstraktion von Leitbahnen für Nerven - nicht ahnend, daß die Laufzeiten der Leitbahnen der entscheidende Schlüssel zur Informatik von Nervennetzen werden könnte.
Anfang der fünfziger Jahre wurde es sogar möglich, unter Verzicht auf Delays und verteilte Leitbahnen künstliche, neuronale Netzwerke lernen zu lassen (Perceptron, Backpropagation...). Man benutzte diskretisierte Zeitfunktionen, die Knotenabstraktion und Clocks (Takte).
Wahrscheinlich geriet Jeffress Modellvorstellung dadurch in Vergessenheit. Lediglich im Bereich akustischer Tierexperimente sind Veröffentlichungen unter Zugrundelegung relativer Zeit in der Folgezeit noch vereinzelt zu finden, wie die von Konishi [1].
Das Genie der Computerpioniere bestand in Hinsicht auf den zu entwickelnden Computer darin, Jeffress Interferenzkreis zu quantisieren. Aus einer Zeitfunktion wurde eine Wertefolge, aus der Verzögerung wurde eine diskrete Folge von Automatenzuständen (states). Die relative Zeit verschwindet unbemerkt aus der Betrachtung. Die Zustandsmaschine (state machine) wird nicht zuletzt dank der automatentheoretischen Grundlagen von Mealy [10], Moore oder Medwedjev zur zeitbestimmenden Abstraktion, zur Abstraktion, die den Computer gebiert.
Merkwürdigerweise ist es 1991 genau die fortgeschrittene Mikroelektronik mit hunderttausenden Transistoren, die eine Rückbesinnung initiiert. Bei einem Prestigeobjekt eines Telekomherstellers (16x16 ATM-Koppelfeld mit 154 MHz-Takt und 860.000 Transistoren) wird dem Team bewußt, daß Gleichzeitigkeit nur noch in Teilen zu erhalten ist.
Das Problem aller Automaten wird zunehmend die über den Takt (clock) herzustellende Gleichzeitigkeit im betrachteten System (Schaltkreis, Leiterplatte). Genau die läßt sich bei immer größeren Schaltungen, immer höheren Taktfrequenzen, dünneren Leitbahnen und immer größeren Flächenwiderständen (R·L/B) der Taktleitungen immer schwerer realisieren.
"Gleichzeitigkeit" gilt nur noch in Teilbereichen schneller und großer Schaltkreise. Zwischen diesen muß entkoppelt werden (asynchrone Kopplungen über Latches, FIFOs etc.). (Noch ist offen, ob die Natur mit bekannten neuronalen Kolumnen einen vergleichbaren Weg einer Teilung zwischen synchronen Kernen und interferentieller Verschaltung einschlug.)
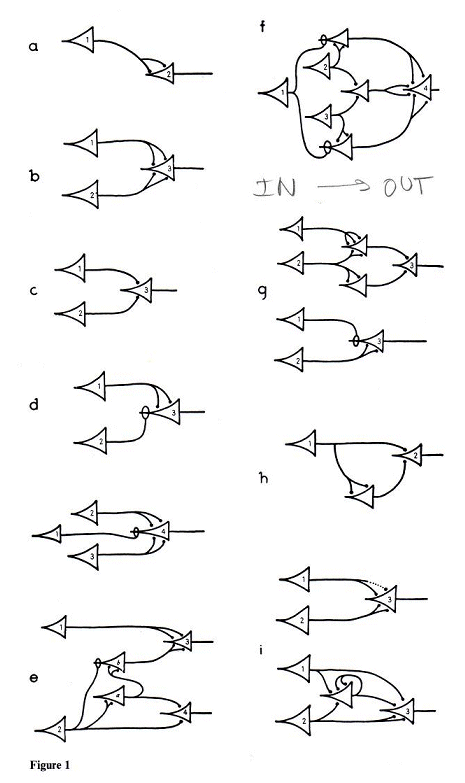
Bild 4: McCulloch-Pitts Darstellung, Bild aus [2]. Man beachte, daß der Informationsfluß gegen die Pfeilrichtung des Symbols geht, der heutige Logik-Inverter zeigt hingegen mit der Spitze in Signalrichtung
Während McCulloch/Pitts ihren Artikel [2] 1943 noch beginnen mit dem Satz:
"The velocity along the axon varies directly with its diameter, from less than one meter per second in thin axons, which are usually short, to more than 150 meters per second in thick axons..."
konzentrieren sie sich eine Seite weiter bereits auf Zustandsfolgen. In den physikalischen Voraussetzungen wird u.a. bereits formuliert:
"...
2. A certain fixed number of synapses must be excited within the period of latent addition in order to excite a neuron at any time, and this number is independent of previous activity and position on the neuron.
3. The only significant delay within the nervous system is synaptic delay.
..."
Diese Abstraktion hat Konsequenzen. Die Zeitachse wird in Zustände (States) zerhackt. Es entstehen zwangsläufig am Ende der Veröffentlichung Terme, die die neue Computerwelt kennzeichnen werden, die aber den Interferenzbezug weitgehend verlieren. Statt eines Ausdruckes in der Form einer Zeitfunktion:
f1(t) = f2(t-T1) + f3(t-T2) + ...
wobei T1 und T2 durch Leitbahndelays entstandene Verzögerungen darstellen könnten, finden wir bei McCulloch/Pitts zu Skizzen neuronaler Verschaltung ausschließlich Ausdrücke der Form
N3(t) :=: .N1(t-1) .v .N2(t-3)
Im Ur-Aufsatz der neuronalen Era [2] wird ein Leitbahn-Delay Tx zu i gerundet (i als ganze Zahl und Zustand: "state"). Die interferenzielle Bedeutung von kleinen Delays zur Ortszuordnung (Jeffress) war unbekannt, Gleitkomma-Verzögerungszeiten wird keine informatische Bedeutung beigemessen.
Im Hinblick auf historisch folgende Automatennetze können wir in der Diskretisierung aufeinanderfolgende Automatenzustände erkennen. Auf der Strecke bleibt aber der Gedanke an Interferenz, an Überlagerung, an Wellenfelder. Die Bedeutung eines Delays Tx (float) als Kennzeichnung des intrinsischen, kontinuierlichen Delays einer nervlichen Leitbahn geht damit verloren. Bis 1993 sollten Delays uninteressant bleiben, und im Schatten der Zustandsautomaten stehen - fernab jeglicher Beziehung zu Wellenfeldern, Projektionen oder Zeitfunktionen. (Das Anfang der Neunziger aufkommende Kapitel des "delay learning" werden wir später besprechen).
Eine Zeitfunktion f(t-Ti) (t floating) wird durch eine Zustands- oder Wertefolge N(i), N(i+1), N(i+2) mit ganzzahligen i abstrahiert - Automatentheorie und Computer konnten entstehen. Kritiker mögen an dieser Stelle anmerken, daß ein Grenzübergang f(t) nach N(i) für große i unproblematisch sei: dem soll nicht widersprochen werden, aber die historische Entwicklung verpaßte offenbar auch diese Möglichkeit.
(Ich bitte um Verzeihung für die Inhomogenität der Notationen. Hier fließen Notationen unterschiedlicher Fachgebiete und Perioden zusammen, die konträrer nicht sein könnten: State Machines - Wellentheorie - Optik. Ich versuche jeweils, nahe am Original zu bleiben).
Im späteren, biologienahen 'Adaline' Neuronenmodell von Widrow und Hoff [3] findet sich z.B. kein Bezug mehr, wenngleich auch hier Zustandsfolgen und Skizzen neuronaler Netze auftauchen. Die Synapse wurde - berechtigterweise oder nicht - als Träger der neuronalen Information erkannt.
Das Delays und Wellen nur eine andere Ausdrucksform einer Folge von Automatenzuständen sein könnten, wurde erst mit dem Daumenexperiment [8] transparent. Selbst modernere Arbeiten [4], die dieses Dilemma charakterisieren, führen noch keine Zeitfunktionen und Wellen ein. Die Wissenschaft blieb über Jahrzehnte in der Automatentheorie stecken.
So gesehen war Jeffress Idee 1947 ein kurzer Gedankenblitz, der aufgrund mangelnder technologischer Relevanz in Vergessenheit geriet.
Auf der anderen Seite hätten die stark biologienahen Modelle der Nobelpreisträger Hodgkin/Huxley (1952) [5] eine Möglichkeit aufzeigen können, interferentielle Projektionen zufällig zu entdecken. Leider aber sind diese Modelle im Detail so stark beladen, daß sich selbst noch 1993 nur einige Dutzend Neuronen auf einmal simulieren ließen. Der Blick auf prinzipielles wurde vom übermächtigen Detail gefressen.
Resümierend ist die Wissenschaftsentwicklung bis zum Ende des vorigen Jahrtausends etwa so zu charakterisieren:
Einerseits (so zeigten meine PSI-Simulationen ab 1995) hat die zeitliche und räumliche Wahl der Quantisierungsintervalle Konsequenzen auf die prinzipielle Erreichbarkeit einer (richtigen) Projektion. Interferenzabbildungen sind so sensibel, daß die Veränderung eines einzigen Parameters sofort die Abbildung zerstören kann.
Andererseits ist ein Rückbezug zur Biologie nur dann möglich, wenn hinreichende, strukturelle Äquivalenz vorliegt. Die tatsächliche Struktur eines Nervennetzes läßt sich aber besser in Delay-Abschnitte als in Zustandsfolgen übersetzen.
Zum Dritten entwickeln sich mit Hilfe von Zeitfunktionen wie im Selbstlauf die physikalischen Eigenschaften, die Laufzeiträume charakterisieren. So erzeugt eine Leitbahnverzweigung, deren Enden gegeneinander gebogen sind, bereits ein (Huygensches) Doppelspaltmuster als Interferenzkartierung entlang der contradirektional verlaufenden Leitbahnen (Man versuche einmal, ein Doppelspaltmuster in einem Automatenmodell physikalisch korrekt (d.h. in Raum und Zeit) zu realisieren. Es zeigt sich, daß die Feinheit der Zeit- und Ortsauflösung darüber entscheidet, ob Simulationen überhaupt sinnvolle Ergebnisse erwarten lassen. Die fatalen Auswirkungen fehlerhaft diskretisierter Orts- und Zeitstruktur auf das Wellenfeld lassen sich z.B. hier [12] studieren). Man erkennt unnatürliche Viereckwellen.
Im Gegensatz zu anderen Arbeiten basierten die hier vorliegenden Untersuchungen auf Zeitfunktionen, deren Verzögerung Tx jeweils die beschrittene Wegstrecke integriert. Folglich existiert kein Leitungspotential, es existieren nur noch (kontinuierliche) Potentiale und Zeitfunktionen diskreter Leitbahnorte (Punkte). Wandert eine Zeitfunktion durch den Raum, so wird ihr dt entsprechend der gültigen Leitgeschwindigkeit v und dem durchschrittenen Wegelement ds integriert mit
dt = ds/v
Entsprechend entstehen zwangsläufig kugelartige Wellen als realistische Ausbreitungsmodelle einer Wellenfront, auch wenn diese im (schroff inhomogenen) Nervennetzwerk eine arge Idealisierung darstellen. Realistisch sollte man sich eher diskrete (eindimensionale) Wellen auf Netzen vorstellen.
Aus dem Nervensystem sind topologie-erhaltende Karten und spiegelverkehrte Projektionen bekannt. Man kennt spiegelverkehrte 'Projektionen', ohne deren Ursachen benennen zu können, man denke z.B. an den Homunculus. (Anmerkung: Der Projektionsbegriff wird sinngemäß auch in anderen Fachgebieten angewandt. Hier aber ist nur die (optische), spiegelverkehrte Abbildung über Wellen und deren Interferenzintegrale gemeint).
Untersuchungen mit pulspropagierenden Netzen zeigten nun, daß vergleichbar zum spiegelverkehrten Abbild, welches z.B. ein optischer Laufzeitraum liefert, Abbildungen in stochastisch verschalteten Netzen durch eine sehr genaue Modellierung mit Wellenfronten simuliert werden können.
Die Konsequenzen seien benannt: Sollte es sich bei biologischen Systemen tatsächlich um Interferenzsysteme handeln, wären nur relativ arbeitende, interferenzielle Meßmittel in der Lage, vermittels interferentieller Rekonstruktion Erregungskartierungen aus diesen Systemen zu gewinnen.
Mit PSI-Tools wurde deshalb in den 90-ern ein Meßsystem entwickelt, welches Informationen aus einem parallelen Laufzeitraum gewinnen und interferenziell verarbeiten hätte können. Leider war die Zeit nur für die akustische Kamera reif. Mehrkanalige Ableitungen von Nerven waren damals nur in unbrauchbaren Qualitäten zu erhalten.
Sollten glückliche Umstände anzutreffen sein, müßte es mit PSI-artigen Tools gelingen, die ersten 'Bilder der Gedanken' rekonstruieren zu können. Sicherlich sollte man sich nicht vorstellen, damit Träume exakt zu dechiffrieren. Vielmehr scheint es realistisch anzunehmen, daß wir mehrfach verzerrte, ineinander verwobene Laufzeiträume vorfinden, deren Kartierungen in ihrer Art als holomorph erscheinen.
Der Interferenzcharakter des Jeffress-Modells offenbart, daß die uns die mit der Leibniz'schen (Boole'schen, binären) Algebra zur Verfügung stehenden Mittel, eine informationelle Aufgabe eines Nervennetzes bestimmen zu können, nicht ausreichen.
Eine Signalverarbeitung kann in einem stochastisch verschalteten, pulspropagierenden Netzwerk nur dort stattfinden, wo sich mehrere Impulse begegnen. Logische Verarbeitung erscheint in Interferenznetzen (IN) folglich ortsgebunden.
Soll heißen: Benachbarte Orte bilden bei identischer Funktion andere Verknüpfungen und andere Ausgaben. Oder: Die Grenzen der Neurochirurgie sind erreicht, werden durch eine Operation die Relativ-Laufzeiten der Fasern in Bezug auf eine neuronale Interferenabbildung signifikant verändert.
Am Beispiel des Zusammenstoßes zweier Autos an einer Kreuzung wird das Problem deutlich: Ein Crash findet nur dann statt, wenn beide Wagen in derselben tausendstel Sekunde am gleichen Ort sind. Würden wir die Zeit diskretisieren (zum Beispiel auf eine Minute), wären bestimmte Crashs nicht möglich. Dafür aber würden neue, vollkommen künstliche entstehen.
Merke: Eine zu grobe Quantisierung der Zeit oder des Ortes verändert die Funktion von Interferenznetzen vollständig!
Da man Interferenznetze nicht so gut mit scharfem Bleistift berechnen kann, wurde seit 1993 ein spezieller Simulator PSI-Tools entwickelt. Dieser gestattete es, einfachste Interferenzkreise parametrisch zu simulieren, wobei die Neuronen im Generator- und Detektorfeld z.B. als Bitmaps definierter Auflösung anordenbar sind. PSI steht für 'Parallele und Serielle Interferenz', damit konnten einfachste Projektionen und Rekonstruktionen berechnet werden. Insbesondere entstanden damit auch (welt-) erste akustische Bilder und Filme.
Funktionen
Resultierende Erregungskarten sind auf zwei Wegen berechenbar: als Interferenzintegrale oder als zeitlich aufgelöste Wellenfelder (Interferenz-Movies). Interferenzintegrale werden bei sonst gleichem Algorithmus bildpunktbezogen berechnet, während I.-Movies zeitschrittbezogen berechnet werden.
Jeder Kanalquell- und Senkenpunkt ist frei im Raum wählbar. Kanaldaten können auf diesem Wege einfach verändert, dupliziert oder summiert werden. Generatorfeld und Detektorfeld sind als Bitmap gestaltet, deren Origin und physische Größe unabhängig von Kanalquellen frei wählbar sind. Matrixraster, Origin, Geschwindigkeit und physische Felddimensionen sind jeweils frei wählbar. Das Timing von Zeitfunktionen kann in der Kanaldatensynthese als Folge von Werten vorgegeben werden. Refrakterität und Pulsabstand können vorgegeben werden.
Jede interferentielle Projektion beteht potentiell aus drei Teilen: Zum einen ist die Rekonstruktion der Quellorte des Generatorraumes für technische Anwendungen interessant (akustische Kamera), siehe Bild 6 oben. Zum zweiten interessiert die Berechnung von Projektionen (Bild 6 unten) in beliebig anders gestaltete Detektorräume z.B. zur Nachrechnung neuronaler Projektionen. Nicht zuletzt existiert auch noch die reale Erregungskarte als Ursprung der Kanaldaten (nicht dargestellt).
Projektion und Rekonstruktion sind innig verbunden. Führen wir PSI-Tools in der Standardform mit inverser Zeit aus, entsteht ein seitenrichtiges Interferenzintegral (Rekonstruktion). Nutzen wir nichtinvertierte Zeit, eintsteht ein spiegelbildliches Interferenzintegral (Projektion); vorausgesetzt, wir wählen identische Ortskoordinaten.
In PSI-Tools existiert deshalb eine Funktion zur Umkehr der Zeitfunktionen der Kanäle: Im Standardfall wird eine Rekonstruktion mit invers laufender Zeitachse und mit den Parametern des Detektorraumes berechnet. Bei zusätzlicher Umkehr der Zeitachse der Kanäle entsteht eine nicht-zeitinvertierte, dafür aber spiegelverkehrte Projektion.
Eigenschaften
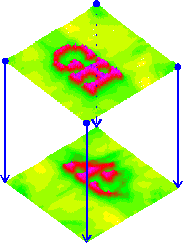
Bild 6: Rekonstruktion (oben) und Projektion (unten) einer Erregungskarte als Interferenzintegral aus denselben, vorab synthetisierten Zeitfunktionen der Kanäle (Kanaldaten), PSI-Tools 1994-1996.
Alle Kanäle besitzen gleiche Verzögerungszeit, die Ausbreitungsgeschwindigkeit ist in beiden Feldern gleich groß. Das Bild erweitert das Konishi-Modell gewissermaßen symbolisch auf vier Kanäle. Es stellt eine interferentielle Abbildung dar, die beide Fragen beantwortet: Gegeben seien vier Zeitfunktionen (blau). Wir sehen oben die Rekonstruktion des Generatorraumes und unten die Projektion in den Detektorraum. Die Rekonstruktion dient also der Ermittlung der Vorlage (oben) und die Projektion der Berechnung des Bildes (unten).
Abbildungsbedingungen können hier bereits erahnt werden:
1) die geometrische Impulslänge (Länge der Pulswelle) muß klein sein gegen die aufzulösende Objektgröße;
2) niedrige Kanalzahlen vorausgesetzt muß der zeitliche Folgeabstand (Refrakterität) zwischen zwei Impulsen groß sein gegen die (zeitliche) Feldausdehnung. Zeit- und Längenmaße sind über die mediale Leitgeschwindigkeit (v = s/t) verbunden.
Neben bildgebenden Elementen können Kanaldaten auch Geräuschamplituden tragen. Ergebnis einer Interferenzanalyse sind unvermeidbar sowohl bildgebende, als auch spektrale Komponenten. Folglich sind sequenzielle Codierungen (Lautbilder) ebenso berechenbar, wie Projektionen und Abbildungen. Wie in der Optik lassen sich beide Komponenten nicht prinzipiell voneinander trennen.
Die zeitliche Komponente äußert sich, wenn Pulse zu kurz nacheinander auf das Feld gelassen werden, z.B. dadurch, daß die Refraktärzeit (die Erholzeit) der übertragenden Axonen zu kurz ist. Dann treten zusätzliche Interferenzen einer Welle mit vorhergehenden und folgenden (anderen) Wellen auf, entsprechend ergibt sich ein Aliasing-Muster im Interferenzintegral.
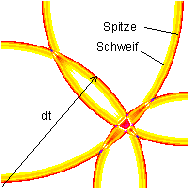
Bild 7: 4-kanaliges Wellenfeld einer Projektion (PSI-Tools, 1995)
Das Bild zeigt eine Projektion einer vierkanalig übertragenen Szene auf ein Empfangsfeld. Die Speisepunkte befinden sich an den Ecken des Feldes. Es ist der Zeitpunkt kurz nach einer Vierfach-Interferenz dargestellt. Siehe auch diese Simulationen. Es wird deutlich, daß nur genau an dem Ort eine höchste Erregung entstehen kann, an welchem sich viele Wellen gleichzeitig begegnen. Zeitliche Relativität von Wellen codiert dann die Funktion des Netzwerkes.
Um zur Titelfrage zurückzukommen: Wenn wir durch den Raum laufende Zeitfunktionen (Wellen) und auf Leitbahnen (Nerven) verteilte Delays als physikalische Realitäten ansehen, dann ist jegliche informatische Funktion in innig verwobenen Nervennetzen nur in Interferenzkreisen denkbar (man denke auch an Redundanz): Folglich gibt es nicht nur Bilder der Gedanken, sondern nahezu alle denkbaren Verarbeitungsvarianten im Nervennetz sind an Projektionen (optischer Art) - also an (spiegel-) bildartige Karten - gebunden: Folglich gibt es nur Bilder der Gedanken als universelles Kommunikationsprinzip des Nervensystems. Die Annahme liegt nahe, daß sie ein motivierter Neuroforscher schon bald nachweisen kann.
Interferenznetze befassen sich folglich mit Eigenschaften zwischen zeitlich relativ aufeinandertreffenden Wellen und deren Interferenzintegralen (umgangssprachlich: mit Bildern aus überlagerten Zeitfunktionen).
Berlin, den 30.9.1995
G. Heinz
[1] Konishi, M.: Die Schallortung der Schleiereule. Spektrum der Wissenschaft, Juni 1993, S. 58 ff.
[2] McCulloch, W.S.; Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5:115-133 ([13], p.18 ff.)
[3] Widrow, B., Hoff, M.E.: Adaptive switching circuits. 1960 IRE WESCON Convention Record, New York: IRE, pp. 96-104 ([13], p.126 ff.)
[4] Rumelhart, D.E., McClelland, J.L.: A Distributed Model of Human Learning and Memory. in: Parallel Distributed Processing. Bradford/MIT Press Cambridge, Massachusetts, vol. 2, eighth printing 1988.
[5] Hodgkin, A.L., Huxley, A.F.: A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. Journ. Physiology, London, 117 (1952) pp. 500-544
[6] Heinz, G., Neuronale Interferenzen. Arbeitsmanuskript, 300 S., 1993
[7] Heinz, G.: Modelling Inherent Communication Principles of Biological Pulse Networks. SAMS 1994, vol.15, no.1, Gordon & Breach Science Publ. UK
[8] Heinz, G.: Relativität elektrischer Impulsausbreitung als Schlüssel zur Informatik biologischer Systeme. 39. Internationales Wissenschaftliches Kolloqium an der TU Ilmenau 27.-30.9.1994, Band 2, S. 238-245
[9] Jeffress, L.A.: A place theory of sound localization. Journ. Comparative Physiol. Psychol., 41, (1948), pp.35–39
[10] Mealy, G.H.: A Method for Synthesizing Sequential Circuits. Bell System Tech. J. 34, Sept. 1955, pp. 1045–1079
[11] Shannon, C.E.: A Mathematical Theory of Communication. Bell System Technical Journal. Short Hills N.J. 27/1948, p. 379–423, 623–656
[12] Alain Destexhe, Diego Contreras, Terrence J. Sejnowski and Mircea Steriade: A model of spindle rhythmicity in the isolated thalamic reticular nucleus. Journal of Neurophysiology 72: 803-818, 1994; zur fatalen Wirkung diskretisierter Zeit siehe (PDF), speziell: (MPG).
[13] Neurocomputing - Foundations of Research. Edited by J.A. Anderson and E. Rosenfeld. The MIT Press, Cambridge MA; London UK, 1988, 729p.
"Wo immer etwas Großes geleistet worden ist auf dem Amboß der Technik, da waren Hammerschläge nötig. Widerstände mußten niedergebrochen, Zeitmeinungen zusammengehämmert werden, damit die neue Form mit unbeugsamer Gestaltungskraft herauswachsen konnte..."
Carl Friedrich Benz
"Wo immer eine gefährlich neue Theorie auftaucht,
wird sie aufs Messer bekämpft.
Deshalb mißtraue dem Lob
und ärgere dich nicht über Ignoranz."
Manfred Frankenfeld
Grundlagen: historic/pressinf/bilder_d.htm
Eigenschaften im Überblick, Movies: historic/index.htm#neuro
Publikationen:
publications/index.htm
PS
Eine Veröffentlichung von Aufsätzen zu IN war anfangs kaum möglich. Die Theorie der IN konnte nicht gelehrt werden, deshalb blieb sie wohl bis heute so unbekannt. Erst die Applikation der IN als akustische Kamera weckte mediales Interesse, siehe Presseseiten. Auch deshalb sind viele der Uraufsätze zu IN nur im WWW zu finden.
gh 2020
Table of Contents Page-URL: historic/intro/intro.htm
Aufsatz ins Web gestellt am 30.9.1995, mehrfach editiert
Visitors since Dec. 2021: