Wie funktioniert unser Gehirn? Wie kann man Nervennetze verstehen? In den letzten zweihundert Jahren haben Wissenschaftler viel über Nerven, Synapsen, Transmitter und Details herausgefunden. Aber obwohl wir zehntausende von Abhandlungen über künstliche neuronale Netze (ANN) sowie hunderte Bücher über Nerven finden, wissen wir bisher eigentlich nichts darüber, wie Nervennetze funktionieren. Was also macht Nervennetze so besonders?
Im Vergleich zu elektrischen Netzwerken sind Nervennetze ganz anders. Während man sich bei den meisten elektrischen Netzwerken (ICs, Computer) wenig Gedanken über eine Verzögerungszeit der Verbindungsleitungen machen muß, sind Verzögerungszeiten von Dendriten und Axonen gigantisch. Wir werden später sehen: Sie sind funktionsbestimmend.
Nebenstehendes Bild zeigt, was passiert, wenn drei Zeitfunktionen von Puls-Bursts wellenförmig sehr langsam über ein Feld von Neuronen fließen. Aufgrund von
Fremdinterferenzen
bilden sich unvermeidbar holografische Strukturen aus. Das "G" erscheint in Fragmenten überall. Siehe dazu auch
Holomorpie und Lashleys Rattenexperimente.
Die "Knotenabstraktion" elektrischer Netzwerke ist damit ungültig für Nerven. Nervliche Pulse werden auf Laufzeitleitungen versendet: Man kann einer Pulswelle bei ihrer Wanderung zusehen. Leitgeschwindigkeiten liegen typisch bei Millimeter bis Meter pro Sekunde, während wir auf der Leiterplatte über etwa 30 ns/m oder 30.000 km/s reden.
Elektronische Signalverarbeitung benutzt Korrelationen für alle Arten von Signalrekonstruktion. Demodulation und Radioempfang nutzen Korrelation mit Schwingkreisen. Jeder Takteingang einer beliebigen integrierten Schaltung oder eines Flip-Flops kann als Korrelator-Eingang angesehen werden. Alle künstlichen neuronalen Netze auf Computern ("Neural Networks (NN)" oder "Artificial Neural Networks (ANN)" oder "Time Delay Networks (TDN)") usw. funktionieren nicht ohne korrelierenden Takt.
Aber Nervennetze haben keinerlei Taktsynchronisation. Sie haben keinen zentralen Takt. Wie könnte unser Kortex also funktionieren? "Künstliche Neuronale Netze" (ANN) zeigen damit im Vergleich zu Nervennetzen ein prinzipiell anderes Verhalten. Um nicht in Konflikt mit NN und ANN zu geraten, bezeichne ich die hier zu untersuchenden, "taktlosen" Netzwerke nervlicher Art seit 1995 als Interferenznetzwerke (IN). Zur Einführung siehe auch einige Animationen zu IN.
Interferenznetze oder -systeme haben einen vergleichbaren mathematisch-physikalischen Hintergrund in verschiedenen Bereichen der Wissenschaft, der von photonischer Welleninterferenz in der Optik über Signalinterferenz in digitalen Filtern (FIR, IIR), Welleninterferenz in Radar- oder Sonargeräten bis hin zu (ionischer) Impulsinterferenz in Nervennetzen reicht. Besondere Eigenschaften sind kurze Wellenlänge, relatives Timing und Nichtlokalität der Funktion.
Wenn wir Interferenzschaltungen mit Impulsen demonstrieren, dann ist zu beachten, dass wir über Wahrscheinlichkeiten von dichtemodulierten Impulsfolgen sprechen. Auch sollten die 1D- und 2D-Anschauungsbeispiele nicht darüber hinwegtäuschen, daß Nervennetze viel komplexer sind.
Wie Karl Pribram bemerkte, wurden die Ideen von "Interferenz" und "Holographie" für Nervennetze 1942 von
Karl Lashley zur Interpretation seiner Rattenexperimente eingeführt, siehe die Note am Ende des Aufsatzes.
Parallel dazu veröffentlichte Lloyd A. Jeffress an der University of Texas in Austin 1947 eine Schaltung zur Schalllokalisation der Schleiereule. Er nannte sie zwar nicht "Interferenzschaltung", aber sie funktioniert als solche. Er interpretierte die horizontale Lokalisation der Ohren durch Korrelation der Geräusche. Die Schaltung kann eine Intuition geben, um die Entwicklung der akustischen Foto- und Kinematographie besser zu verstehen.
Denkt man an den pulsartigen Charakter und die langsamen Impulsgeschwindigkeiten auf Nerven, so findet man Eigenschaften, die mit optischen Projektionen (Bildern) vergleichbar sind. Im Gegensatz zu ANN bekommen unsere IN höchste Bedeutung bei Projektionen von Bildern durch Nervennetze. "Denken" ist nur "in Bildern oder Zeichen" möglich, nicht in Zahlen oder Bits. Oder wie schon C.S. Peirce (1837-1914) feststellte: "All thought is in signs".
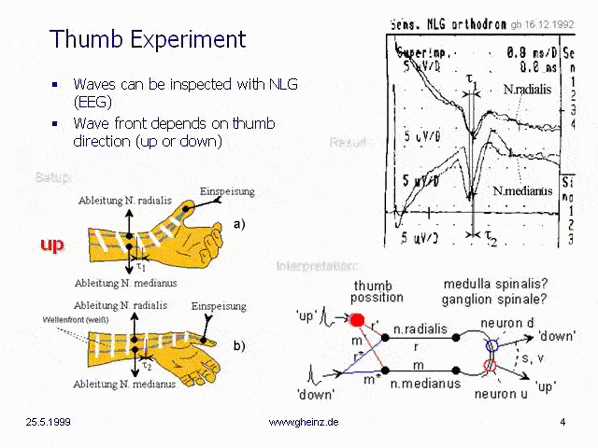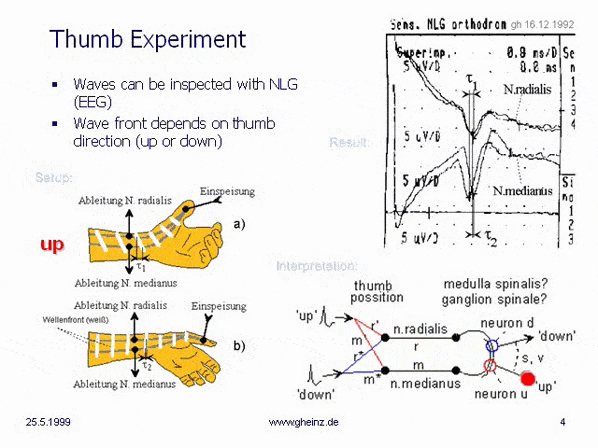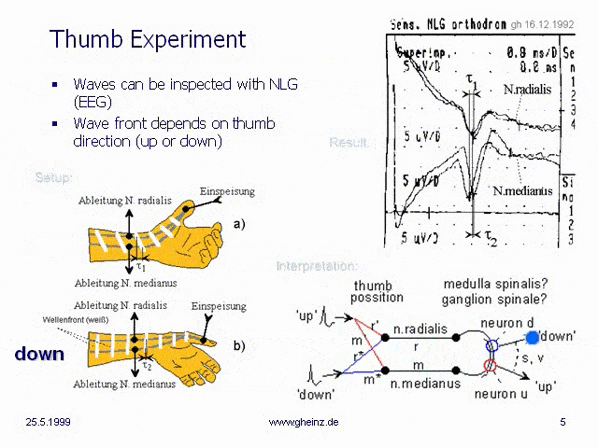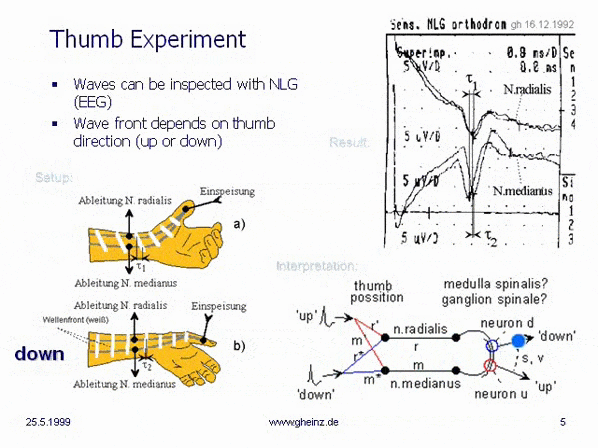
Zu Weihnachten 1992 zeigte das sog. "Daumenexperiment" , dass unser Nervensystem tatsächlich als Interferenzsystem arbeiten kann. Jetzt stand die Tür offen! Nach diesem erfolgreichen Experiment untersuchte ich verschiedene Eigenschaften von "Wellen auf Leitbahnen". Innerhalb kurzer Zeit entstand das Buch "Neuronale Interferenzen" (NI93). Eine kurze Übersicht über dessen Ergebnisse finden Sie hier.
Um Interferenzen (Überlagerungen) zu erhalten, brauchen wir so etwas wie "Wellen auf Leitbahnen". Können wir solche Wellen an irgendeinem Nervennetz direkt beobachten? In der Tat, das können wir!
Andrew Packard untersuchte 1995
Farbwellen auf Tintenfischen. Er schnitt das Rückenmark an einer Seite durch. Stehende Farbmuster veränderten sich zu spontanen, farbigen Erregungswellen, siehe seine Filme. Der "Packard-Gletscher" in der Antarktis wurde nach ihm benannt.
Wie können wir uns die Funktion eines Interferenznetzwerks (IN) vorstellen? Die nächste Schaltung (Quelle NI93) zeigt ein einfachstes IN. (In IN haben Leitbahnen sehr begrenzte Leitgeschwindigkeiten - es sind keine elektrischen Knoten!) Ein Neuron im Senderaum S darf an der Position P feuern. Die Impulse laufen zu und über die beiden Kanäle A und A' in den Empfangsraum M. Dort treffen sie sich bei P' wieder. An allen anderen Orten erscheinen die Pulse nacheinander, nicht gleichzeitig. An Stellen gleichzeitigen Eintreffens ist die Chance am höchsten, ein Neuron zu erregen.
Dabei bekommt das empfangende Neuron den höchsten Erregungswert, bei dem beide Schwesterimpulse genau zur gleichen Zeit eintreffen. Wenn das Neuron bei P feuert, wäre dies das Neuron an der Position P'. Wir erkennen: Ein biologisches Interferenznetzwerk überträgt Informationen als gespiegelte Projektion vom Generatorraum S in den Detektorraum M.
Um die spontanen Wellen auf Andrew's Tintenfischen zu verstehen: Durchtrennen wir Kanal A, verschwindet jede Projektion. Wenn Leitbahn A durchtrennt wird und einen statisch hohen Pegel bekommt, laufen jetzt nur noch die über A' kommende Wellen durch den Detektorraum - wir sehen Wellen statt feststehende Erregungsorte.
Lashleys
Hologramm-Idee, Jeffress
Geräuschortung, Packards
Wellen auf Tintenfischen, das
Daumenexperiment und ein
bildhaftes,
holographisches
Verhalten zeigen also die Richtung der Nervennetzforschung an: Wir haben Wellen-Interferenz-Schaltungen zu untersuchen, um Nervennetze zu verstehen. Das sind Schaltungen, die ohne jede Taktsynchronisation Projektionen (wie optische Bilder) über Leitbahnen transportieren.
So verfolgte die Arbeit seit 1993 parallel zwei Richtungen: die Rekonstruktion von nervlichen Daten (EKG, EEG, ECoG) und von Schall (akustische Bilder & Filme). Diesem Weg folgend, machten wir in einem kleinen Team zusammen mit Sabine Höfs und Carsten Busch im August 1994 erste passive (stehende) akustische Bilder. Dazu koppelten wir Mikrofone an einen selbstgebauten EEG-Datenrekorder. Diese wurden mit dem ersten Rechenprogramm (dem "Bio-Interface") zur Berechnung von Interferenzbildern gewonnen.
Es war die Geburtsstunde der Akustischen Foto- und Kinematographie (Akustische Kameras), die mit Innovationspreisen ausgezeichnet wurde und weltweit hunderte Arbeitsplätze schuf.
Ein weiterer technischer Hintergrund von Interferenzen erschließt sich bei mathematischer Betrachtung von Rauschsignalen für unsichtbares RADAR oder das Nervensystem, siehe die Faltung von Rauschsignalen. Lassen Sie uns deshalb Interferenzintegrale und Interferenzmuster näher betrachten.
Karl Lashley fand mit seinen Rattenexperimenten eine hologrammartige Eigenschaft des Gehirns. Unabhängig davon, welchen Teil des Gehirns er entfernte, konnten sich die Ratten an ein zuvor erlerntes Verhalten erinnern, was in Aufsätzen seit 1929 veröffentlicht wurde. In seiner 1950 erschienenen Arbeit "In search of the engram" (Quelle p.478-505) schrieb er:
"It is not possible to demonstrate the isolated localization of a memory trace anywhere within the nervous system." (p.501)
(Es ist nicht möglich, eine isolierte Lokalisierung einer Gedächtnisspur irgendwo innerhalb des Nervensystems zu demonstrieren.)
Karl Pribram schrieb mir, daß Lashley einen Scherz pflegte: Seine Rattenexperimente würden beweisen, daß sich das Gedächtnis der Ratten nicht in deren Cortex befindet.
Schon im GFaI-Jahresbericht 1994
(PDF)
zeigte die Rekonstruktion von Zeitfunktionen hologrammartige
Muster (v=200)
als eine immanente Eigenschaft von IN, siehe Bild rechts (v ist die Leitgeschwindigkeit).
Der Hintergrund dafür ist in der Pulsdichte zu suchen. Wenn jedes Neuron des Generatorraumes nicht nur einmal feuert, sodern fortfolgend, dann treffen Wellen i mit Wellen i+1, i-1 etc. zusammen. Damit entstehen mehrfache Bilder im Detektorraum an verschiedenen Orten, siehe Fremdinterferenzen.
Dabei bestimmt allein der Pulsabstand den Abstand der vielfach auftretenden Bilder, siehe Fremdinterferenzradius.
Hologramme erscheinen deshalb als unabwendbares Naturgesetz durch Fremdinterferenzen um den Ort der Selbstinterferenz herum, mehr dazu siehe z.B. hier.
Wir diskutierten Ergebnisse mit Karl Pribram (1919-2015). Er schickte mir damals diesen Auszug seines geplanten Buches 'Brain and Being' zu wichtigen Details:
"Lashley hatte vorgeschlagen, dass Interferenzmuster zwischen Wellenfronten in der elektrischen Aktivität des Gehirns auch als Substrat von Wahrnehmung und Gedächtnis dienen könnten. Das entsprach meinen früheren Intuitionen, aber Lashley und ich hatten diese Alternative wiederholt diskutiert, ohne auf eine Idee zu kommen, wie Wellenfronten im Gehirn aussehen könnten. Wir konnten auch nicht herausfinden, wie sie, wenn es sie gäbe, irgendetwas auf der Verhaltensebene erklären könnten. Die Diskussionen, die zwischen 1946 und 1948 stattfanden, wurden etwas unangenehm im Hinblick auf
Donald Hebb's Buch
("The Organization of Behavior", 1949),
das er zu der Zeit schrieb, als wir alle zusammen im Yerkes Laboratory for Primate Biology in Florida waren. Lashley mochte Hebbs Formulierung nicht, konnte aber seine Gründe für diese Meinung nicht ausdrücken:
"Hebb is correct in all his details, but he's just oh so wrong."
Wenige Tage nach meiner zweiten Begegnung mit Ernest Hilgard brachte Nico Spinelli, ein Postdoktorand in meinem Labor, einen Artikel von John Eccles (Scientific American, 1958) mit, in dem er feststellte, dass wir Synapsen zwar nur einzeln untersuchen könnten, aber präsynaptische verzweigte Axone bilden synaptische Wellenfronten. Funktionell sind es diese Wellenfronten, die berücksichtigt werden müssen. Mir wurde sofort klar (siehe Abb. 1-14, Languages of the Brain 1971), dass Axone, die aus verschiedenen Richtungen in die synaptische Domäne eindringen, Interferenzmuster erzeugen würden.
(Es war eine dieser Gelegenheiten, bei denen man sich wie ein absoluter Idiot fühlt. Als Antwort auf Lashlys und meine erste Frage, wo die Wellen im Gehirn wären, starrte er uns ins Gesicht und wir hatten nicht den Geist, es während all der Jahre der Diskussion herauszufinden.)"
(Karl Pribram in
'Brain and Being', 2004, Ch.12: 'Brain and Mathematics', page 217 ff. See his preview, page 4 ff)
Der Konfliktpunkt war folgender. Donald Hebb schrieb in seinem Buch:
"When one neuron repeatedly assists in firing another, the axon of the first cell develops synaptic knobs (or enlarges them, if they already exist) in contact with the soma of the second cell"
("Wenn ein Neuron wiederholt dabei hilft, ein anderes zu befeuern, entwickelt das Axon der ersten Zelle synaptische Noppen (oder vergrößert sie, falls sie bereits vorhanden sind) in Kontakt mit dem Soma der zweiten Zelle").
Dieser Satz wurde zur Leitidee von Lernalgorithmen der (künstlichen) neuronalen Netzwerktheorie (NN, ANN).
Aber warum war Hebb in allen Details korrekt, aber er lag "ach so falsch"?
Es sollte 45 Jahre dauern, um präzise Antworten zu finden. Sie lauten etwa:
Lernen ist nur dann möglich, wenn die Struktur zeitlicher Verzögerungen des Netzwerks dafür sorgt, daß an dem Neuron, das etwas tun oder lernen soll, die über verschiedene Wege von der Quelle kommenden Partialimpulse zeitgleich ankommen.
Wie ist das zu verstehen? Warum sollten Verzögerungen über Gewichte dominieren? Schauen wir uns dazu nochmals das Titelbild des Buches "Neuronale Interferenzen" [NI93] von 1993 an. Jeder aus dem sendenden Feld S kommende Impuls erreicht zwar irgendwann jedes Neuron im empfangenden Feld M. Aber die Erregbarkeit eines Neurons ist umso höher, je mehr Pulse es zeitgleich erreichen. Einzelimpulse gehen unter. Damit sind zeitgleich ankommende Pulse im Vorteil. Deshalb haben wir uns auf diese zu konzentrieren. Dargestellt sind deshalb nur die Fälle, in denen je zwei Impulse von oben zeitgleich ein Neuron unten erreichen.
Soweit, so gut. Was aber bedeutet das? Das am weitesten links liegende, sendende Neuron kann nur dem am weitesten rechts liegenden, empfangenden Neuron eine Botschaft senden (die von diesem verarbeitet werden kann). Es ist prinzipiell nicht in der Lage, einem ebenfalls links oder einem mittig liegenden, empfangenden Neuron eine Botschaft zukommen zu lassen: Die Verzögerungsstruktur verhindert das. Wir sehen: "Delays dominate over weights".
Somit können nicht alle Neuronen des Netzwerkes miteinander kommunizieren. Im Beispielbild sind Neuronen, die miteinander kommunizieren können, spiegelbildlich angeordnet, die Pfeile P und P' sollen das verdeutlichen.
Während bei einer Hausklingelanlage die zwischen den Tastern und den Klingeln verlegten Kabel die Kommunikationsverbindung herstellen, stellt in einem Interferenznetzwerk die Verzögerungsstruktur die Kommunikationsverbindung zwischen Quelle und Ziel her.
Wenn also ein Neuron (bedingt durch die Verzögerungsstruktur des Netzes) nicht den Ort hat, um die Teilimpulse einer Quelle (gleichzeitig) zu erhalten, kann von diesem Sender nicht viel empfangen werden! Anders gesagt: Hebb'sches Gewichtslernen ist unmöglich ohne eine dafür geeignete Verzögerungsstruktur.
Ein tieferer Hintergrund ist auch der, dass Neuronen nicht von direkten Nachbarn erregt werden dürfen. Um Selbsterregung des gesamten Netzwerks zu verhindern, erzeugen Verzögerungsstrukturen ohne zutun auch Nachbarschaftshemmung.
Obwohl er es noch nicht präzise ausdrücken konnte, hatte Karl Lashley die richtige Intuition!
Mehr dazu siehe "Holomorphie und Lashleys Rattenexperimente" (Link), NI93, Kap.5, S.117 , Kap.10, S.211 oder einen Aufsatz von 2018, Kap.7, S.9.
Ein Überblick zu Eigenschaften von Interferenzintegralen ist hier zu finden
english /
german.
Visitors since Dec. 2021:
Aus dem Englischen rückübersetzt von www.DeepL.com/Translator mit manuellen Korrekturen